Aufgaben zur Berechnung von Längen im Koordinatensystem
Lerne hier, den Abstand zwischen Punkten zu berechnen und die Länge von Strecken im Koordinatensystem zu bestimmen.
- 1
Berechne die Länge der Strecke mithilfe der angegebenen Koordinaten
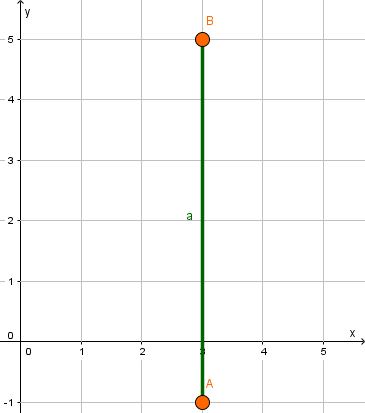
A(2|8), B(2|2)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Längen im Koordinatensystem
Trage die gegebenen Punkte in ein Koordinatensystem ein.
Der Punkt A liegt höher als der Punkt B. Außerdem ist die Strecke [AB] parallel zur y-Achse, weil die Punkte A und B den gleichen x-Wert (Rechtswert) haben.
Berechne die Länge der Strecke [AB], indem du den y-Wert des unteren Punktes von dem y-Wert des oberen Punktes subtrahierst.
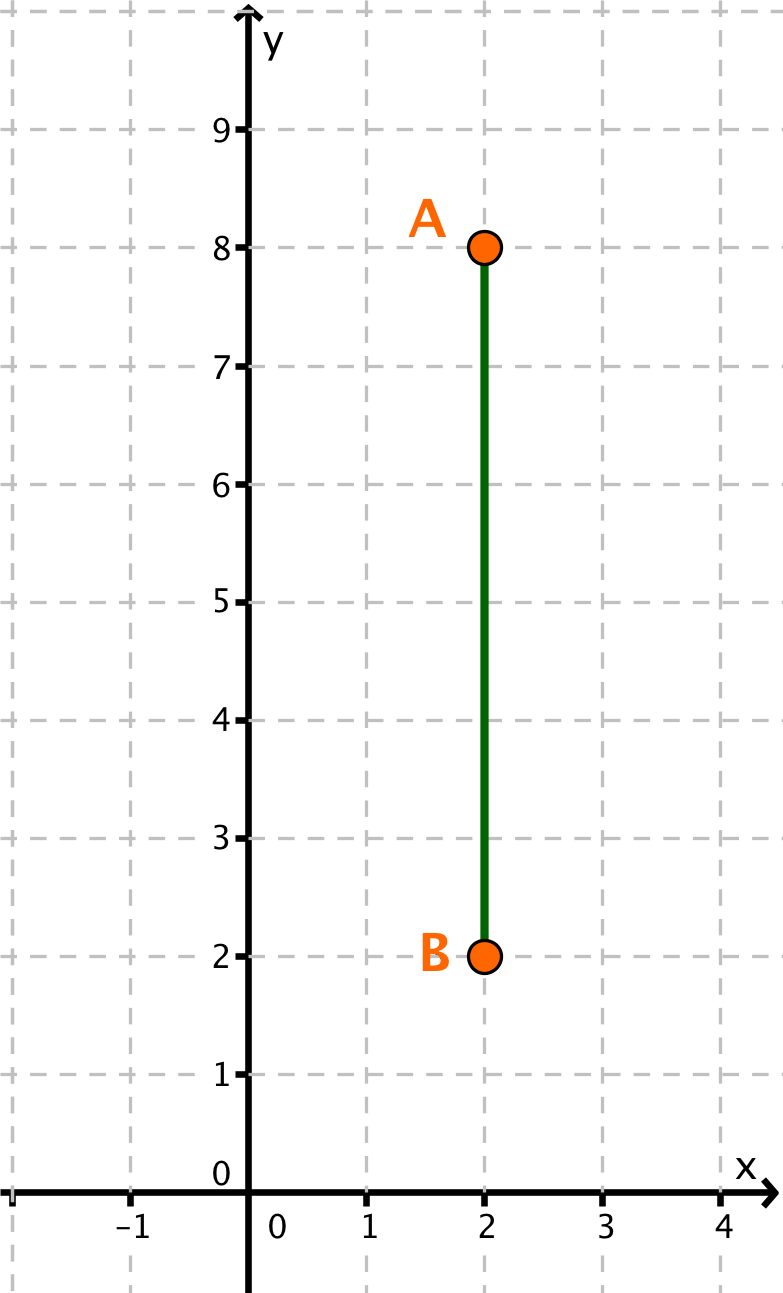
Setze nun die y-Koordinaten von A und B ein.
Antwort: die Strecke [AB] hat die Länge 6.
Hast du eine Frage oder Feedback?
A(-3|-2), B(5|-2)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Längen im Koordinatensystem
Trage die Punkte A und B in ein Koordinatensystem ein.
Der Punkt B liegt rechts von dem Punkt A. Außerdem ist die Strecke [AB] parallel zur x-Achse, da die beiden Punkte den gleichen y-Wert (Hochwert) haben.
Berechne die Länge der Strecke [AB], indem du den x-Wert des Punktes, der weiter links liegt (), von dem x-Wert des Punktes, der weiter rechts liegt (), subtrahierst.
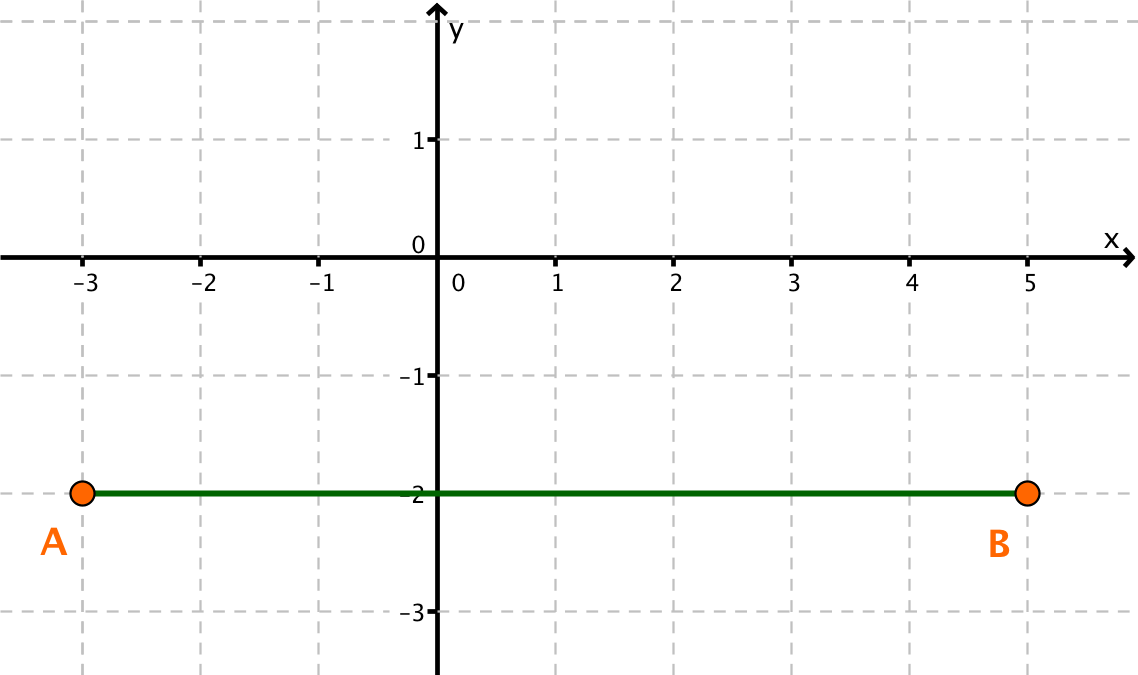
Setze die gegebenen x-Werte ein.
Antwort: Die Strecke [AB] hat die Länge 8.
Hast du eine Frage oder Feedback?
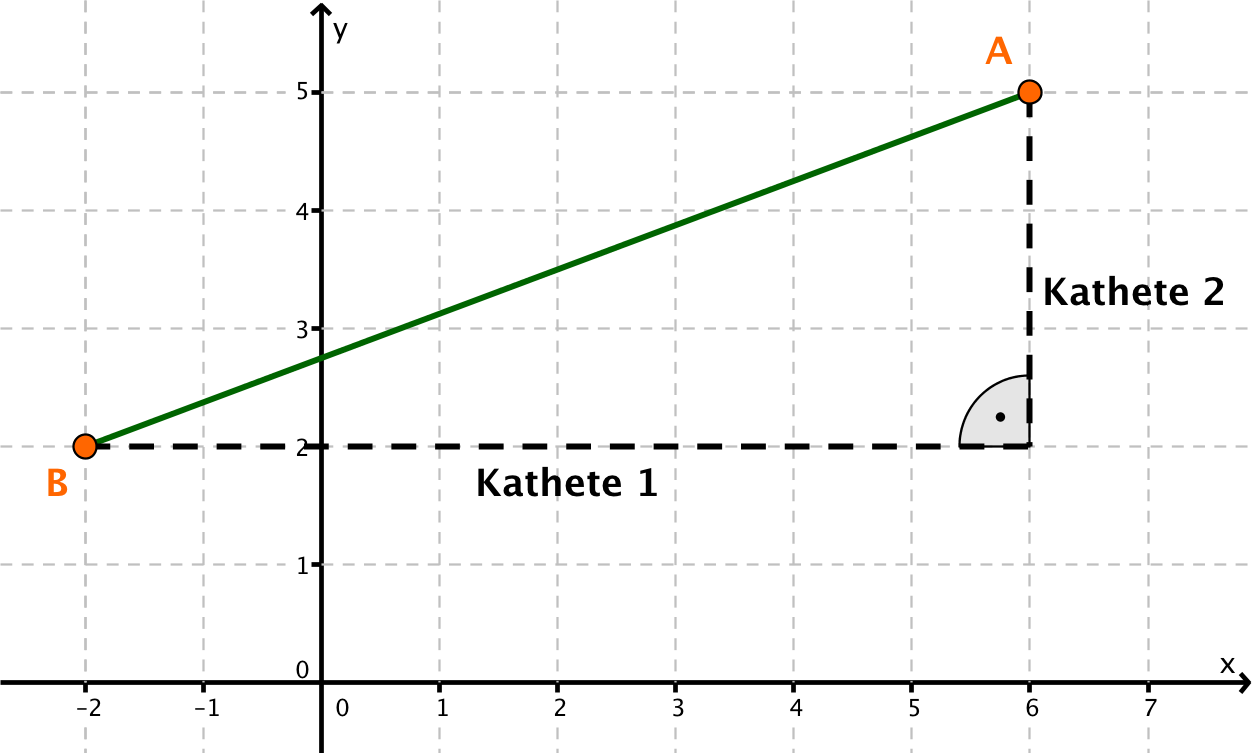
A(-2|3), B(1|-1)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Längen im Koordinatensystem
Trage die Punkte in ein Koordinatensystem ein.
Berechne die Länge der Katheten. Die Kathete 1 ist parallel zur x-Achse und die Kathete 2 ist parallel zur y-Achse.
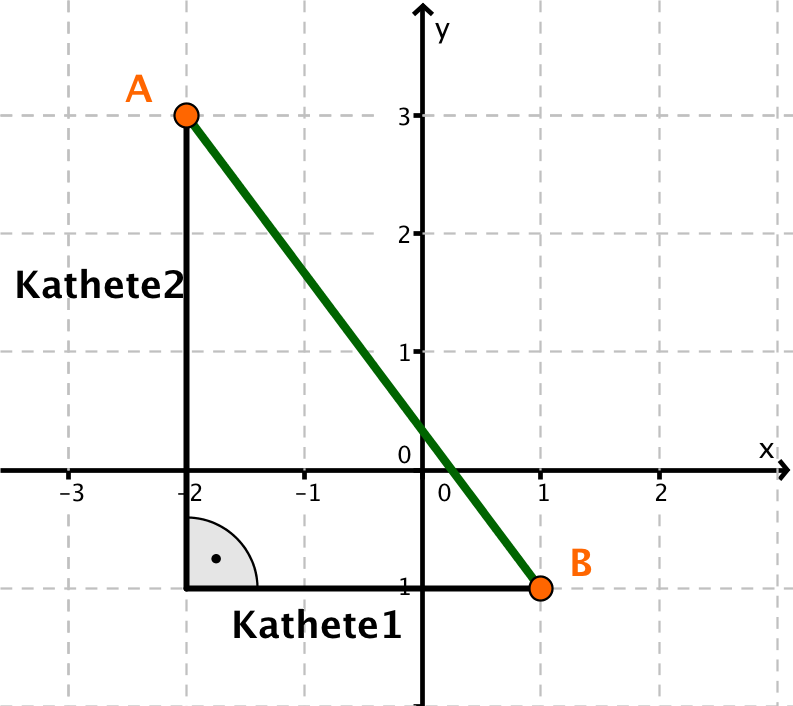
Wende den Satz des Pythagoras an. Die gesuchte Strecke ist die Hypotenuse.
Die Strecke [AB] hat die Länge 5.
Hast du eine Frage oder Feedback?
- 2
Berechne die Länge der Strecke .
Lies die Koordinaten der Punkte und aus dem Koordinatensystem ab.
und
Der Punkt liegt höher als der Punkt . Berechne nun die Länge der Strecke [], indem du den -Wert des unteren Punktes von dem -Wert des oberen Punktes subtrahierst.
Setze die gegebenen Koordinaten der Punkte ein.
Antwort: Die gegebene Strecke hat die Länge 6.
Hast du eine Frage oder Feedback?
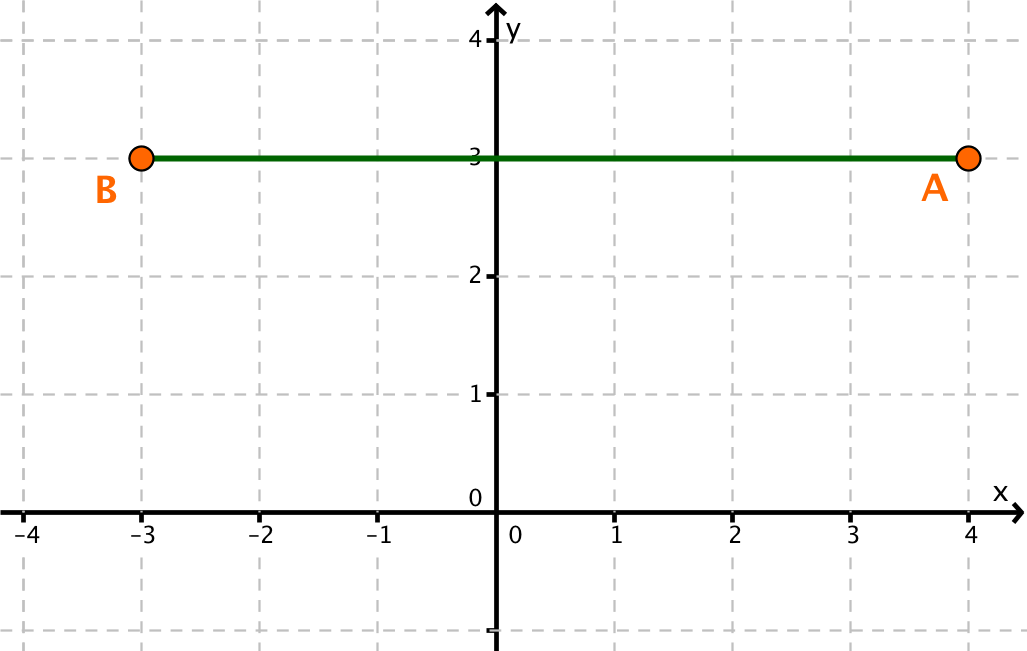
Lies die Koordinaten der Punkte und aus dem Koordinatensystem ab.
und
Setze die Koordinaten von und ein.
Antwort: Die Strecke hat die Länge .
Hast du eine Frage oder Feedback?
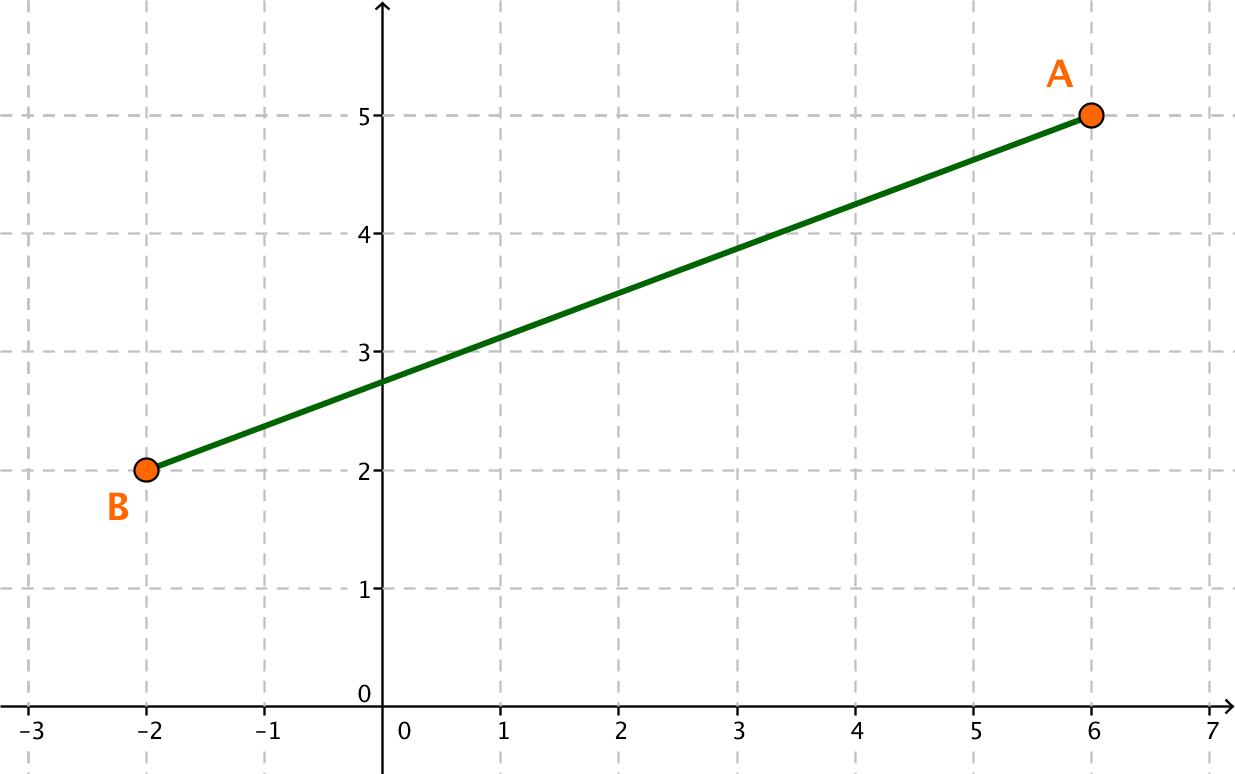
Lies die Koordinaten der Punkte und aus dem Koordinatensystem ab.
und
Die Länge der Strecke wird mit dem Satz des Pythagoras berechnet. Die gesuchte Strecke ist die Hypotenuse eines rechtwinkligen Dreiecks.
Berechne nun die Länge der Strecke mit dem Satz des Pythagoras.
Setze die errechneten Längen der Katheten ein.
Ziehe nun auf beiden Seiten der Gleichung die Wurzel
Antwort: Die Strecke hat die Länge .
Hast du eine Frage oder Feedback?
- 3
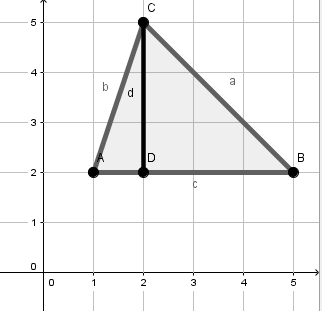
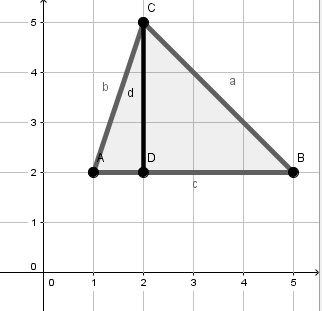
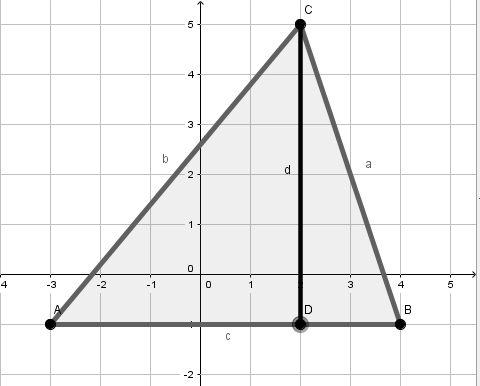
Berechne die Längen der Strecken a,b,c und d
Für diese Aufgabe benötigst Du folgendes Grundwissen: Längen im Koordinatensystem
In der Grafik sieht man, dass die Seiten c und d parallel zu den Achsen liegen.
Da die Seite d parallel zur y-Achse ist, verwenden wir die Formel
Die Seite c ist parallel zur x-Achse, also verwendet man die Formel
Die Seiten a und b liegen nicht parallel zu den Achsen. Deshalb verwendet man Pythagoras, um die Längen zu berechnen.
Hast du eine Frage oder Feedback?
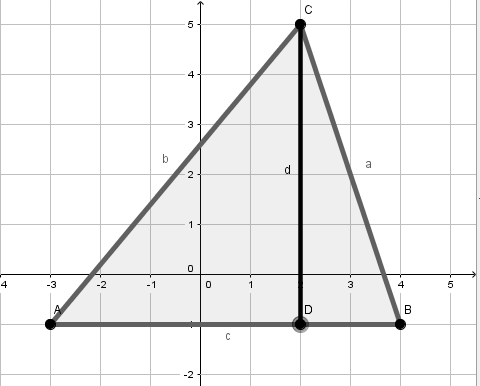
Für diese Aufgabe benötigst Du folgendes Grundwissen: Längen im Koordinatensystem
In der Grafik sieht man, dass die Seiten c und d parallel zu den Achsen liegen.
Da die Seite d parallel zur y-Achse ist, verwenden wir die Formel
Die Seite c ist parallel zur x-Achse, also verwendet man die Formel
Die Seiten a und b liegen nicht parallel zu den Achsen. Deshalb verwendet man Pythagoras, um die Längen zu berechnen.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?