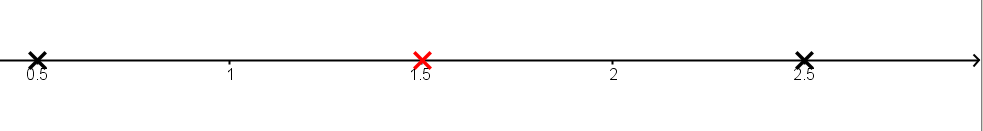Bestimme den Scheitelpunkt der Funktion mit der Funktionsgleichung anhand ihrer Nullstellen.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?