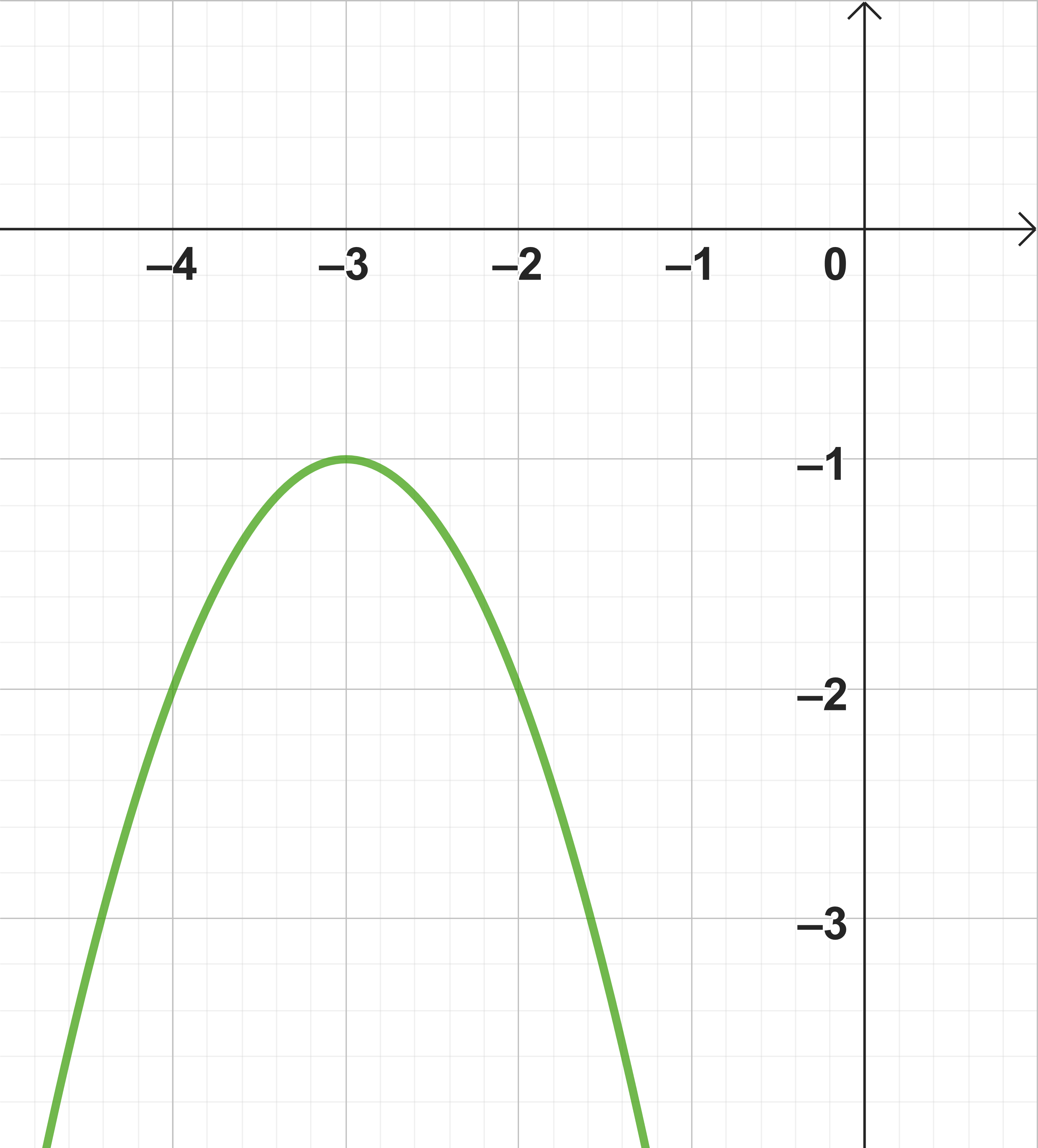
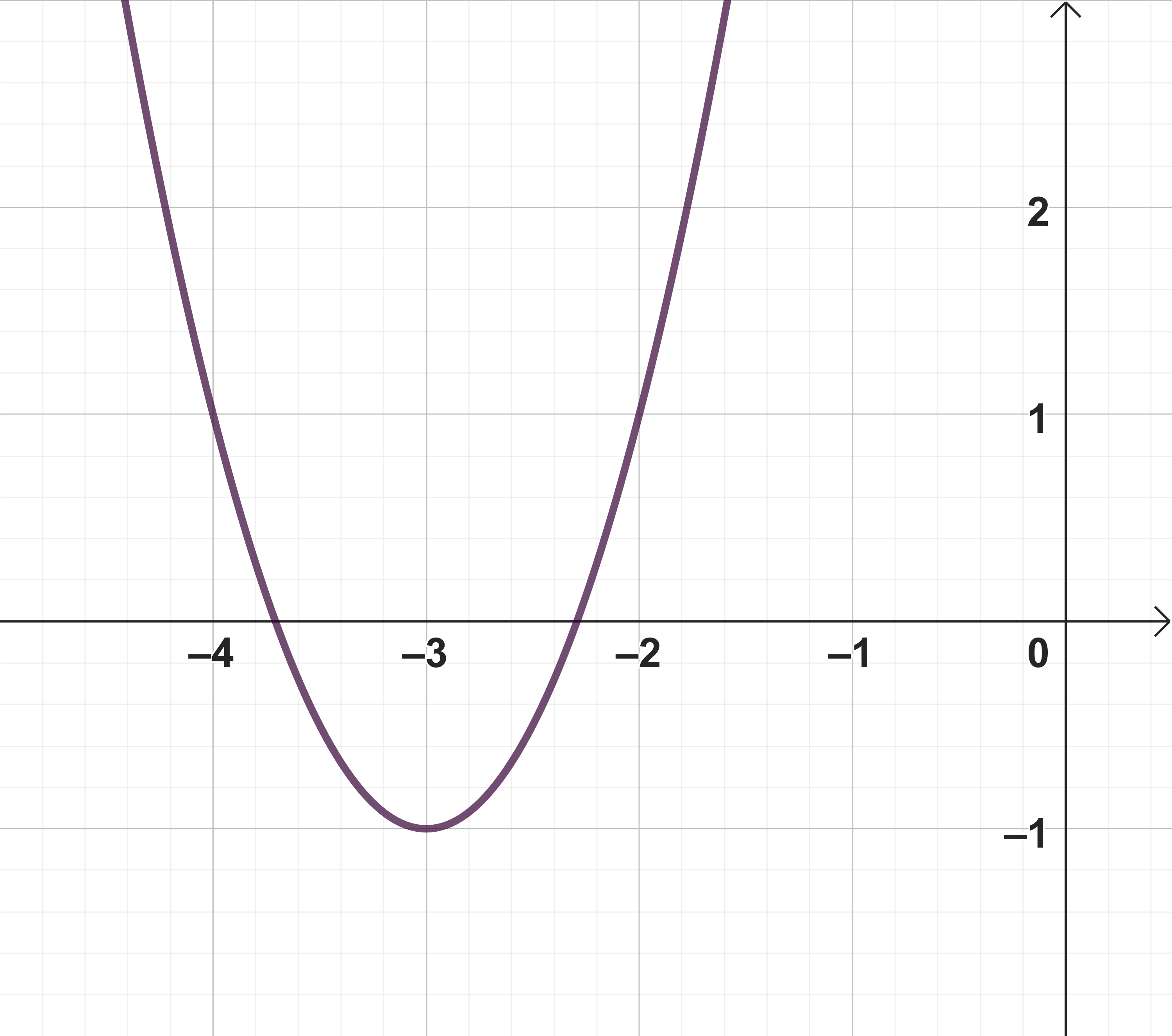
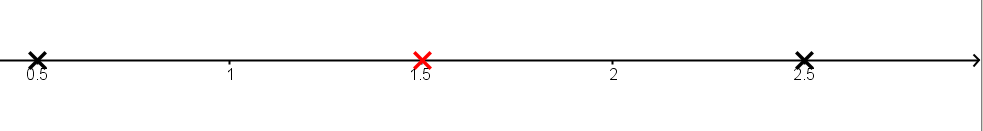Aufgaben zur Berechnung des Scheitelpunktes

Hier findest du Aufgaben zum Berechnen des Scheitelpunkts einer Parabel. Schaffst du sie alle?

1
Scheitel und Scheitelform
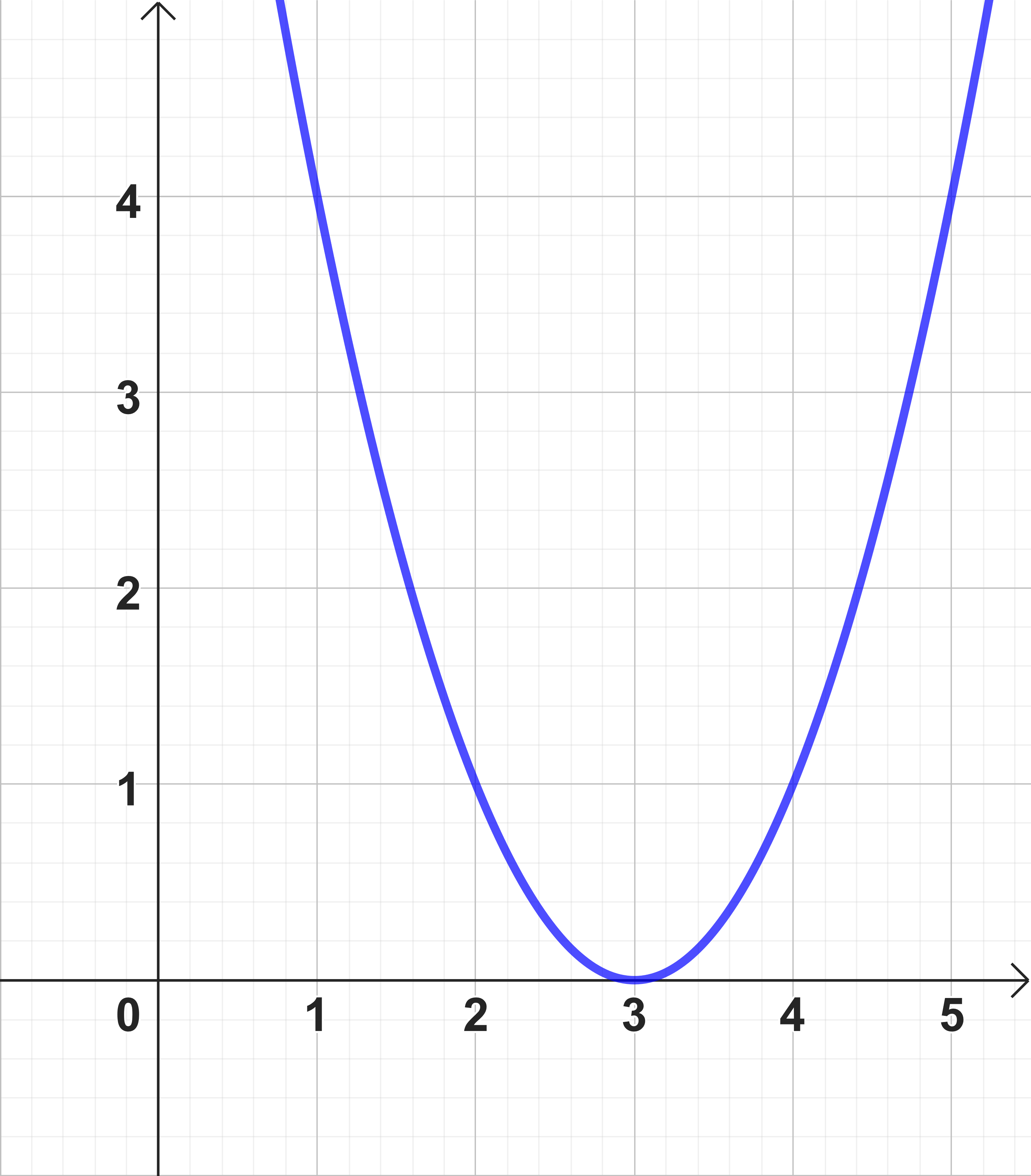
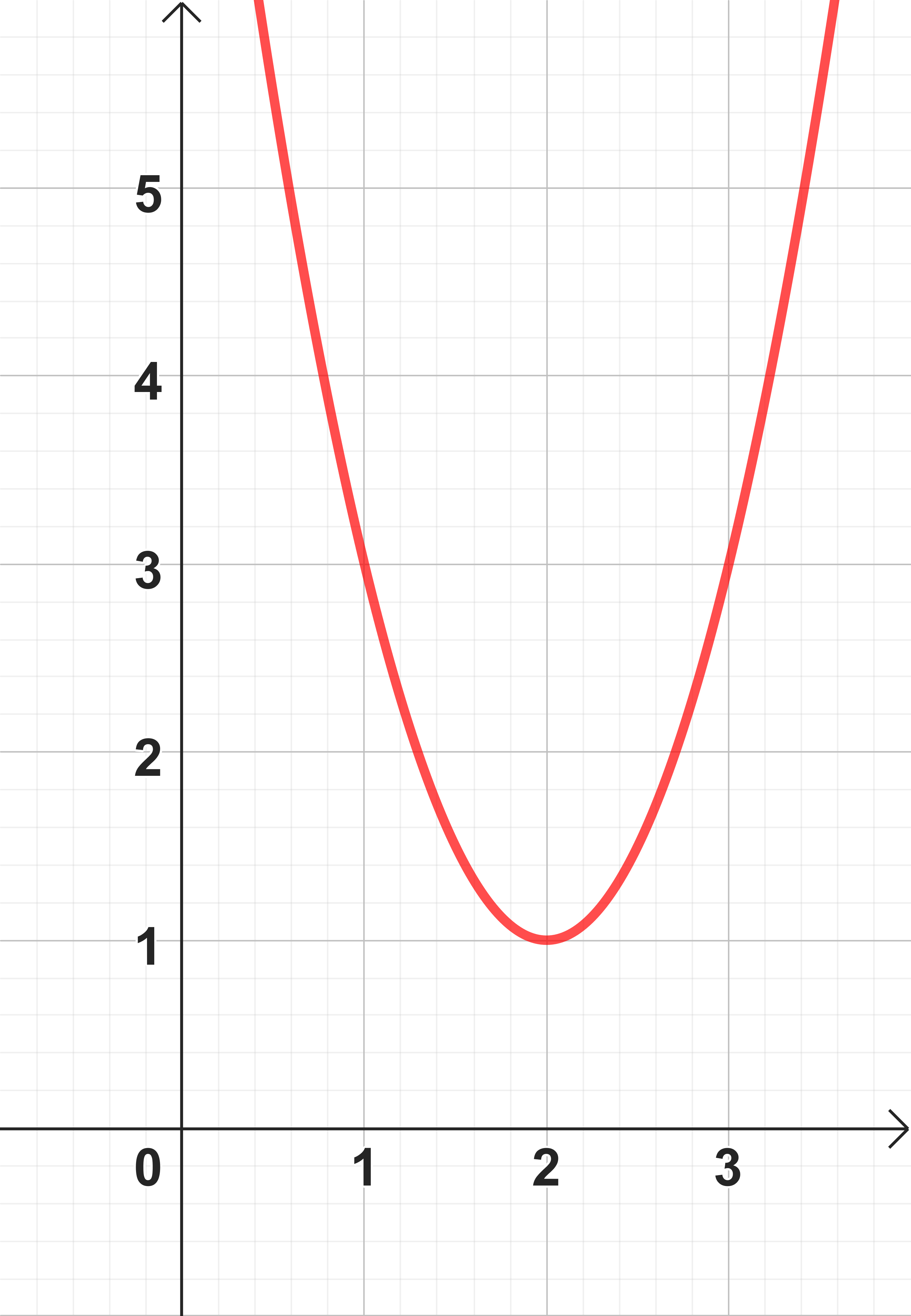
Bestimme den Scheitel und die Scheitelform der Parabel. Ordne die Zahlenwerte richtig zu.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform einer Parabel
Lösung
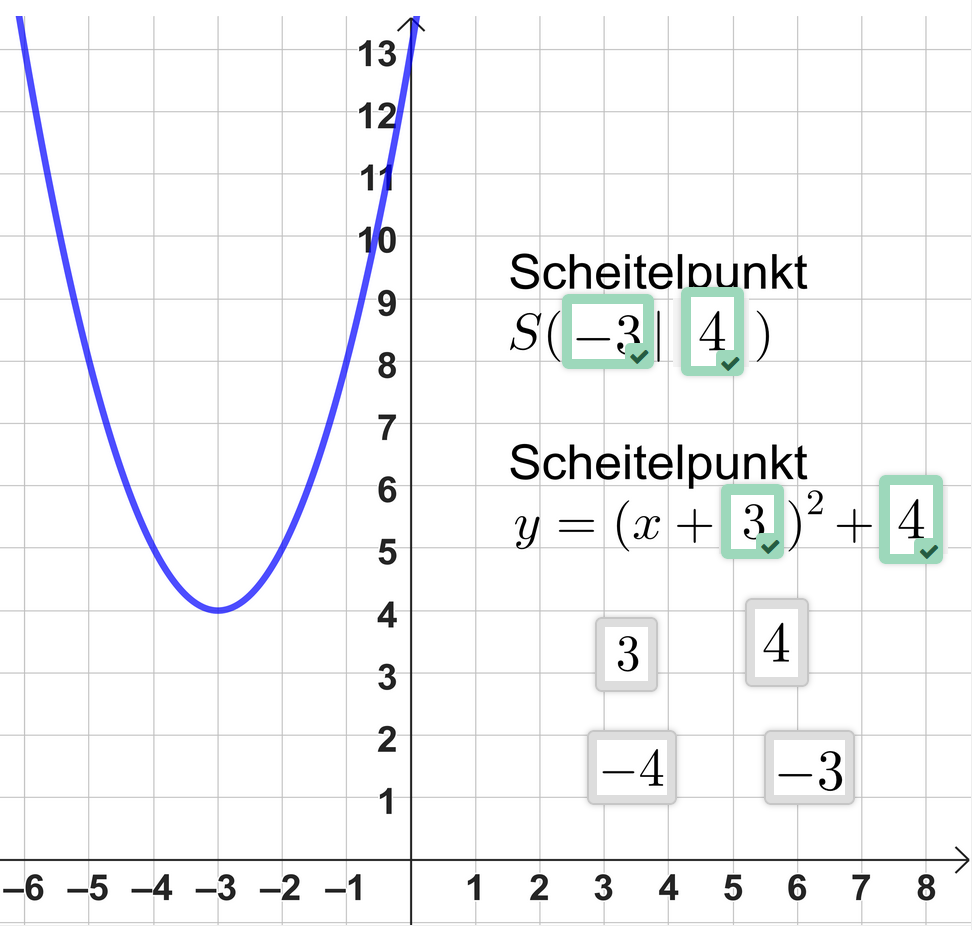
Richtige Zuordnung
Lies den Scheitel an dem Graphen im Koordinatensystem ab.
Setze die Koordinaten in den Scheitelpunkt ein.
Beim Einsetzen der Werte in die Scheitelform ändert sich die $x$ -Koordinate.
2
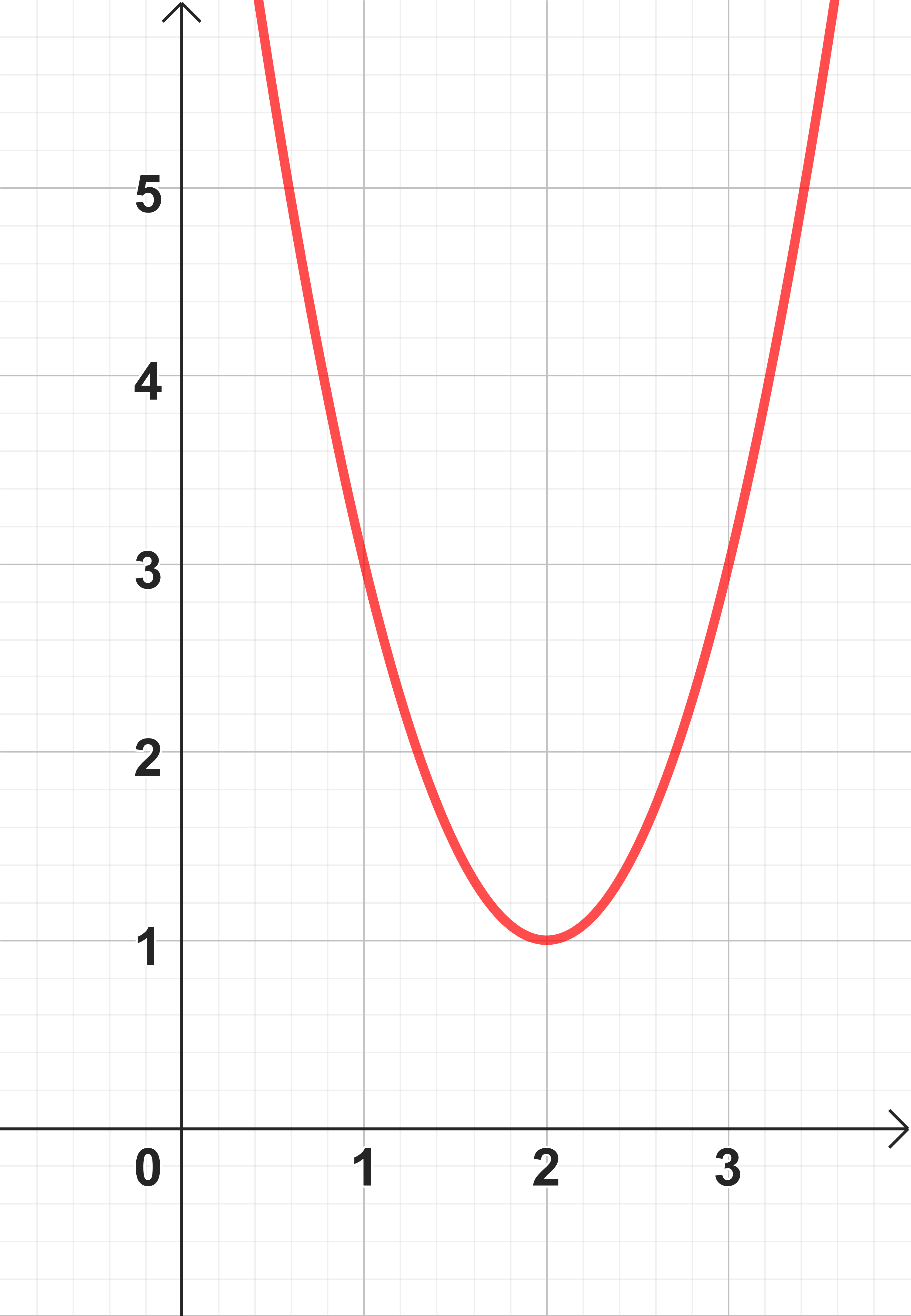
Bestimme mithilfe der Scheitelform den jeweiligen Scheitelpunkt der folgenden Funktionen.
Gib den Scheitelpunkt nach folgendem Beispiel an:
$S (1,2; 3)$ oder $S (1,2 | 3)$ .
1. $f (x) = {(x - 4)}^{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
  $f (x) = (x - 4)^{2}$
  Die Funktionsgleichung befindet sich bereits in Scheitelform (Scheitelpunktsform): $f (x) = a (x - d)^{2} + e$ .
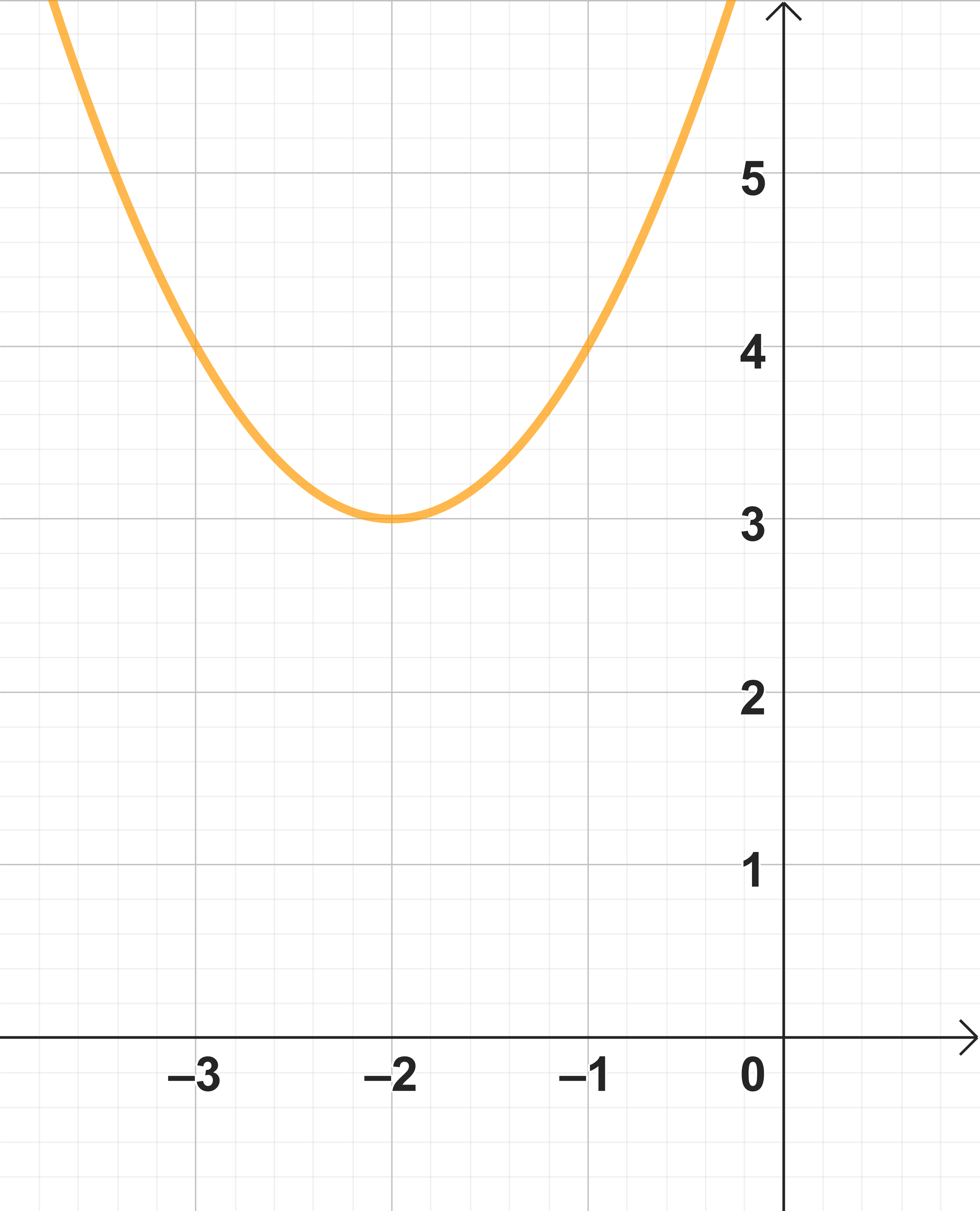
  Lies die Parameter $a, d, e$ vom gegebenen Graphen ab.
  $a = 1$ , $d = 4$ und $e = 0$
  Damit ergibt sich der Scheitelpunkt als $(d | e)$ .
  $S = (d | e) = (4 | 0)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f (x) = {(3 + x + 2)}^{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
  $f (x) = (3 + x + 2)^{2}$
  Vereinfache die Funktionsvorschrift.
  $\begin{array}{l} f (x) = (3 + x + 2)^{2} \\ = (x + 5)^{2} \end{array}$
  Die Funktion ist in Scheitelpunktform: $f (x) = a (x - d)^{2} + e$ . Lies den Scheitelpunkt ab.
  $\Rightarrow S = (- 5 | 0)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f (x) = x^{2} + 2 x + 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
  Du kannst den Scheitelpunkt finden, indem du die Parabel auf Scheitelform bringst und daraus den Scheitelpunkt abliest:
  $f (x) = x^{2} + 2 x + 1$
  Wende die 1. binomische Formel an.
  $\begin{array}{l} f (x) = x^{2} + 2 x + 1 \\ = {(x + 1)}^{2} \end{array}$
  Die Funktion hat nun die Scheitelform.
  Lies den Scheitelpunkt ab.
  $\Rightarrow S = (- 1 | 0)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
Gib jeweils die Koordinaten des Scheitels an.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
1. $f (x) = {(x - 2)}^{2} + 1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
  $f (x) = (x - 2)^{2} + 1$
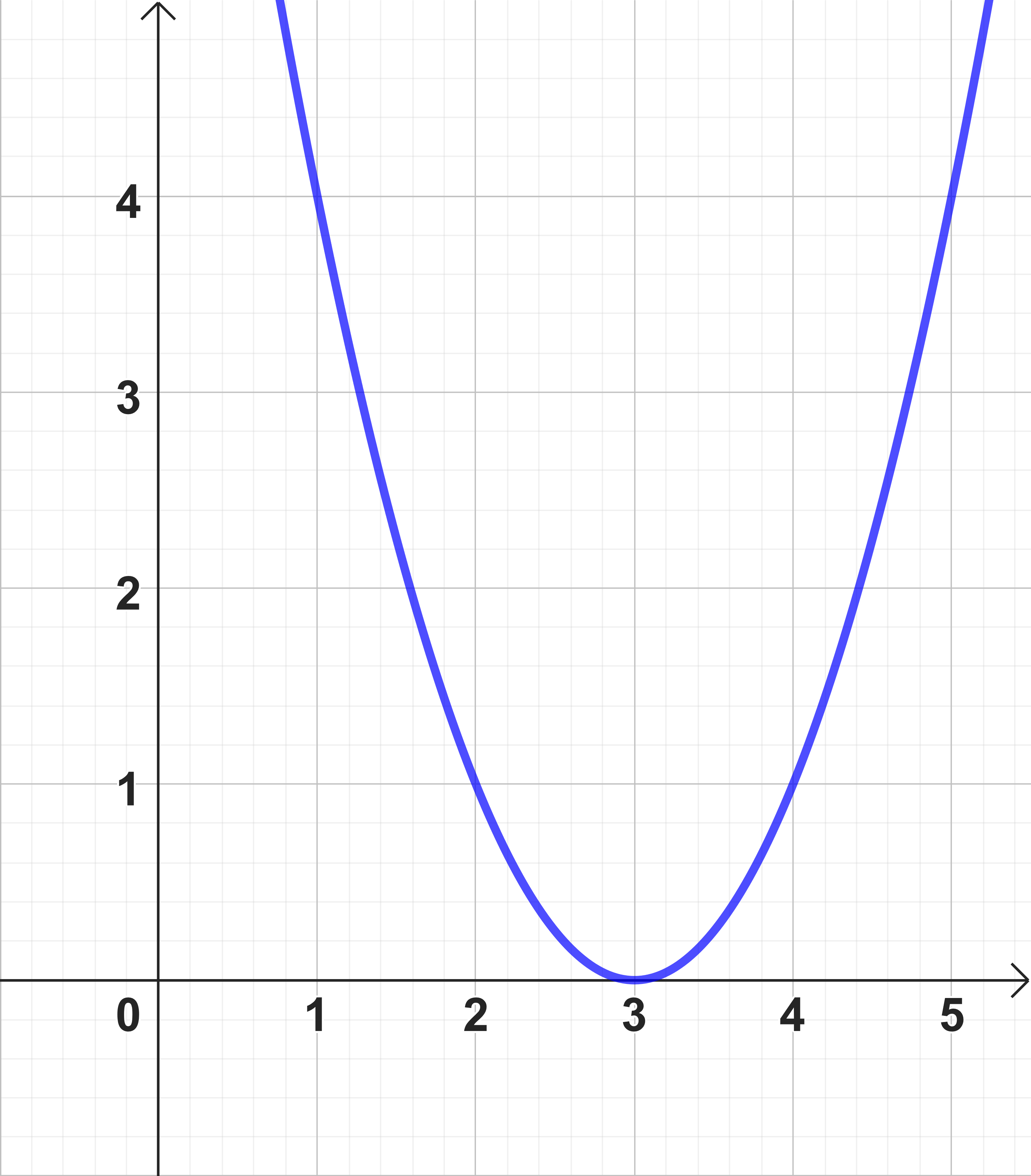
  Die Abbildungsvorschrift ist bereits in Scheitelform. Lies die Parameter $a$ , $d$ und $e$ aus der Formel der Scheitelform.
  $a = 1$ , $d = 2$ und $e = 1$
  Der Scheitelpunkt ergibt sich als $S (d | e)$ .
  $\Rightarrow S (2 | 1)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f (x) = - 12 + {(x + 8)}^{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
  Die Abbildungsvorschrift ist bereits in Scheitelform, es sind lediglich die beiden Summanden vertauscht. Vertausche deshalb zuerst die Summanden
  $\begin{array}{l} f (x) = - 12 + (x + 8)^{2} \\ = {(x + 8)}^{2} - 12 \end{array}$
  Lies die Parameter $a$ , $d$ und $e$ aus der Scheitelform ab.
  $a = 1$ , $d = - 8$ und $e = - 12$ .
  Den Scheitelpunkt erhältst du als $S (d | e)$
  $\Rightarrow S (- 8 | - 12)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f (x) = x^{2} - 4 x + 4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: allgemeine Form und Scheitelform
  In dieser Aufgabe kannst du entweder mit der Scheitelform oder allgemeinen Form rechnen.
  1. Möglichkeit: Lösen anhand der Scheitelform
  $f (x) = x^{2} - 4 x + 4$
  Wende die 2. binomische Formel an.
  $\begin{array}{l} f (x) = x^{2} - 4 x + 4 \\ = {(x - 2)}^{2} \end{array}$
  Jetzt kannst du den Scheitelpunkt ablesen, da die Funktion in Scheitelform ist.
  $\Rightarrow S (2 | 0)$
  2. Möglichkeit: Lösen anhand der allgemeinen Form
  $f (x) = x^{2} - 4 x + 4$
  Bestimme $a$ , $b$ und $c$ aus der allgemeinen Form.
  $a = 1, b = - 4, c = 4$
  Nun kannst du diese in die Formel $S (- \frac{b}{2 \cdot a} | c - \frac{b^{2}}{4 a})$
  einsetzen.
  $S (- \frac{(- 4)}{2 \cdot 1} | 4 - \frac{(- 4)^{2}}{4 \cdot 1})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S (2 | 0)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $f (x) = x^{2} + 2 x - 3$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: allgemeine Form und Scheitelform
  1. Möglichkeit: Lösung anhand der Scheitelform
  $f (x)$ $=$ $x^{2} + 2 x - 3$
  ↓
  Ergänze die Funktion quadratisch.
  $=$ $x^{2} + 2 x + 1 - 1 - 3$
  ↓
  Benutze die 1. binomische Formel.
  $=$ ${(x + 1)}^{2} - 4$
  Da die Parabel jetzt in Scheitelform ist, kannst du den Scheitelpunkt ablesen.
  $\Rightarrow S (- 1 | - 4)$
  2. Möglichkeit: Lösung anhand der allgemeinen Form
  $x^{2} + 2 x - 3$
  Bestimme $a$ , $b$ , $c$ aus der allgemeinen Form.
  $a = 1$ , $b = 2$ , $c = - 3$
  Setze $a$ , $b$ , $c$ in die Formel ein.
  $S (- \frac{2}{2 \cdot 1} | - 3 - \frac{2^{2}}{4 \cdot 1})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S (- 1 | - 4)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $f (x) = {(3 - x)}^{2}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
  In dieser Aufgabe ist die Parabel schon beinahe in Scheitelform gegeben; die restlichen nötigen Umformungen lauten:
  $f (x)$ $=$ ${(3 - x)}^{2}$
  ↓
  Klammere (-1) aus.
  $=$ ${((- 1) (x - 3))}^{2}$
  ↓
  Quadriere die einzelnen Faktoren.
  $=$ ${(x - 3)}^{2}$
  Lies den Scheitelpunkt ab.
  $\Rightarrow S (3 | 0)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Bestimme den Scheitelpunkt der folgenden Funktionen.

Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).

$f (x) = 3 {(x - 2)}^{2} - 4$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
Gegeben ist $f (x) = 3 (x - 2)^{2} - 4$
Die Funktion $f (x)$ liegt bereits in Scheitelform vor. Lies die Parameter $a$ , $d$ und $e$ der Scheitelform ab.
$a = 3$ , $d = 2$ und $e = - 4$
Dann ist $S (d | e)$ der Scheitelpunkt von $f$ .
$\Rightarrow S (2 | - 4)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
$f (x) = 2 ({(x + 1,5)}^{2} + 1)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
$f (x)$ $=$ $2 ({(x + 1,5)}^{2} + 1)$
$=$ $2 {(x + 1,5)}^{2} + 2$
Lies den Scheitelpunkt ab.
$\Rightarrow S (- 1,5 | 2)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$f (x) = 2 x^{2} - 4,8 x + 0,88$

$f (x) = (x - 2) (x + 3)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
1. Möglichkeit: Lösung anhand der Scheitelform
$f (x)$ $=$ $(x - 2) (x + 3)$
↓
Multipliziere aus
$=$ $x^{2} + x - 6$
↓
Ergänze quadratisch.
$=$ $x^{2} + 2 \cdot \frac{1}{2} x + (\frac{1}{2})^{2} - (\frac{1}{2})^{2} - 6$
↓
Verwende die 1. binomische Formel
$=$ ${(x + 0,5)}^{2} - 6,25$
Lies nun den Scheitelpunkt ab.
$\Rightarrow S (- \frac{1}{2} | - 6 \frac{1}{4})$
2. Möglichkeit: Lösung anhand der allgemeinen Form
$f (x)$ $=$ $(x - 2) (x + 3)$
↓
Multipliziere aus.
$=$ $x^{2} + x - 6$
Bestimme $a$ , $b$ , $c$ aus der allgemeinen Form.
$a = 1$ , $b = 1$ , $c = - 6$
Setze $a$ , $b$ , $c$ in die Formel ein.
$S (- \frac{1}{2 \cdot 1} | - 6 - \frac{1^{2}}{4 \cdot 1})$
Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
$\Rightarrow S (- \frac{1}{2} | - 6 \frac{1}{4})$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

5
Bestimme den Scheitelpunkt der Funktion $f$ mit der Funktionsgleichung $f (x) = x^{2} + 4 x - 5$ anhand deren Nullstellen.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Parabel
$f (x) = x^{2} + 4 x - 5$
Berechne die Nullstellen von $f$ , z.B. mit der PQ-Formel:
$x = - 2 \pm \sqrt{2^{2} - (- 5)}$
$= - 2 \pm \sqrt{9}$
$= - 2 \pm 3 \in {- 5, 1}$
Da $f$ ein Polynom zweiten Grades ist, hat es höchstens zwei reelle Nullstellen. Somit sind $- 5$ und $1$ genau die Nullstellen von $f$ .
$f (x) = 0 \Leftrightarrow$
$x^{2} + 4 x - 5 = 0 \Leftrightarrow$
$x \in {- 5,1}$
Der $x$ -Wert $x_{s}$ des Scheitels liegt genau mittig zwischen diesen beiden Nullstellen.
Also ist $x_{s} = \frac{- 5 + 1}{2} = \frac{- 4}{2} = - 2$ .
Bestimme nun den $y$ -Wert des Scheitels, indem du den $x$ -Wert $x_{s}$ in die Funktionsgleichung von $f$ einsetzt:
$\begin{array}{rcl} f (x_{s}) & = & f (- 2) \\ = & (- 2)^{2} + 4 \cdot (- 2) - 5 \\ = & 4 - 8 - 5 \\ = & - 9 \end{array}$
Der Scheitelpunkt von $f$ ist also $S = (- 2 | - 9)$ .
6
Bestimme den Scheitelpunkt der Funktion $f$ mit der Funktionsgleichung $f (x) = - 2 x^{2} + 6 x - 2,5$ anhand ihrer Nullstellen.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Parabel
$f (x) = - 2 x^{2} + 6 x - 2,5$
Berechne die Nullstellen von $f$ , z.B. mit der Mitternachtsformel:
$\begin{array}{rcl} x_{1 / 2} & = & \frac{- 6 \pm \sqrt{6^{2} - 4 \cdot (- 2) \cdot (- 2,5)}}{2 \cdot (- 2)} \\ = & \frac{- 6 \pm \sqrt{36 - 20}}{- 4} \\ = & \frac{- 6 \pm \sqrt{16}}{- 4} \\ = & \frac{- 6 \pm 4}{- 4} \\ ⟹ x_{1} & = & \frac{1}{2}, x_{2} = \frac{5}{2} \end{array}$
Da $f$ ein Polynom zweiten Grades ist, hat es höchstens zwei reelle Nullstellen.
Die Nullstellen von $f$ sind also $0,5$ und $2,5$ .
Der $x$ -Wert des Scheitels $x_{s}$ liegt genau in der Mitte dieser beiden Nullstellen.Die Zahl $1,5$ liegt zwischen $0,5$ und $2,5$ .
Also ist $x_{s} = \frac{0,5 + 2,5}{2} = \frac{2}{3} = 1,5$ .
Bestimme nun den $y$ -Wert des Scheitels, indem du den $x$ -Wert in die Funktionsgleichung von $f$ einsetzt.
$f (x_{s}) = f (0) = - 2 \cdot (1,5)^{2} + 6 \cdot 1,5 - 2,5 = 2$
Der Scheitelpunkt von $f$ ist demnach $S = (1,5 | 2)$ .
7
Gib die Koordinaten des Scheitels folgender Funktionen an.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
1. $g_{1} : x \mapsto x^{2} - 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
  $g_{1} (x) = x^{2} - 2$
  Die Funktion ist schon in Scheitelpunktform gegeben. Lies den Scheitelpunkt ab.
  $\Rightarrow S = (0 | - 2)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $g_{2} : x \mapsto x^{2} + 1,2 - 0,4$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
  $g_{2} (x) = x^{2} + 1,2 - 0,4$
  Vereinfache den Term und lies den Scheitelpunkt ab.
  $\begin{array}{l} g_{2} (x) = x^{2} + 1,2 - 0,4 \\ = x^{2} + 0,8 \end{array}$
  $\Rightarrow S = (0 | 0,8)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Bestimme den Scheitelpunkt:

Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).

strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
$f (x) = x^{2} - 3 x - \frac{3}{4}$ (mit quadratischer Ergänzung)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
$f (x)$ $=$ $x^{2} - 3 x - \frac{3}{4}$
↓
Ergänze quadratisch.
$=$ $x^{2} - 2 \cdot 1,5 x + {1,5}^{2} - {1,5}^{2} - \frac{3}{4}$
↓
Fasse zur 2. binomischen Formel zusammen.
$=$ ${(x - 1,5)}^{2} - 2,25 - \frac{3}{4}$
↓
Fasse zusammen.
$=$ ${(x - 1,5)}^{2} - 3$
↓
Lies den Scheitel ab.
$\Rightarrow S (1,5 | - 3)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$f (x) = - \frac{1}{4} x^{2} + 6 x - 11$

$f (x) = \frac{1}{2} x^{2} + 4 x - 24$ (mit Hilfe der Nullstellen)

$f (x) = - 2 x^{2} + 8 x + 10$

$f (x) = 3 x^{2} - 4 x + 18$

$f (x) = - 5 x^{2} - x - 2$

$f (x) = 2 x + 0,1 x^{2} - 10$

$f (x) = \frac{1}{2} x^{2} + 3 x - 4$

$f (x) = \frac{2}{3} x^{2} + 8 x$

$f (x) = \frac{5}{6} x^{2} + x - 1$

$f (x) = - 0,5 x^{2} + 20 x - 30$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
$f$ ist ein Polynom zweiten Grades, hat also zwei Nullstellen $x_{1}, x_{2}$ . Sind diese reell, so liegt der Scheitelpunkt $x_{s}$ aufgrund der Symmetrie von $f$ genau mittig zwischen ihnen: $x_{s} = \frac{x_{1} + x_{2}}{2}$ .
Bestimme zunächst die Nullstellen von $f$ :
$f (x) = - 0,5 x^{2} + 20 x - 30 = 0$
Wende die Mitternachtsformel an.
$x_{1} = \frac{- 20 + \sqrt{20^{2} - 4 \cdot (- 0,5) (- 30)}}{2 \cdot (- 0,5)} = + 20 - \sqrt{340}$
$x_{2} = \frac{- 20 - \sqrt{20^{2} - 4 \cdot (- 0,5) (- 30)}}{2 \cdot (- 0,5)} = 20 + \sqrt{340}$
$x_{1}$ und $x_{2}$ sind damit reelle Zahlen und es gilt:
$x_{s} = \frac{x_{1} + x_{2}}{2} = \frac{40}{2} = 20$
Setzt man den $x$ -Wert $x_{s}$ des Scheitelpunktes in die Funktionsvorschrift ein, so erhält man dessen $y$ -Wert:
$f (x_{s}) = f (20) = - 0,5 \cdot 20^{2} + 20 \cdot 20 - 30 = - 200 + 400 - 30 = 170$
$\Rightarrow S (20 | 170)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

$f (x) = - \frac{3}{4} x^{2} + x$

$f (x) = 10 x^{2} + 100$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt bestimmen
$f (x) = 10 \cdot x^{2} + 100$
An dieser Funktionsvorschrift kannst du den Scheitelpunkt sofort ablesen, da sie schon in Scheitelpunktform gegeben ist.
$\Rightarrow S (0 | 100)$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

9
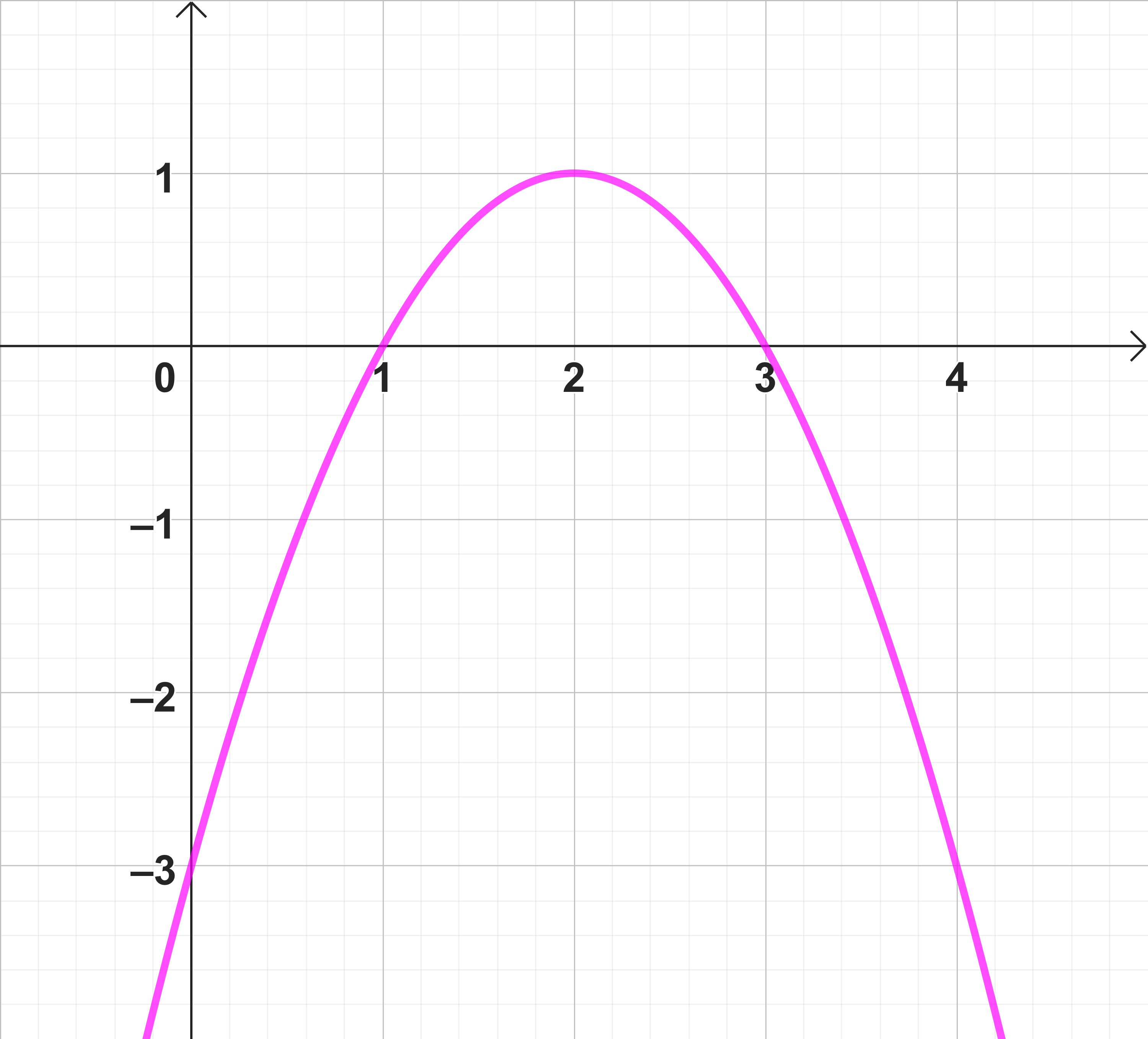
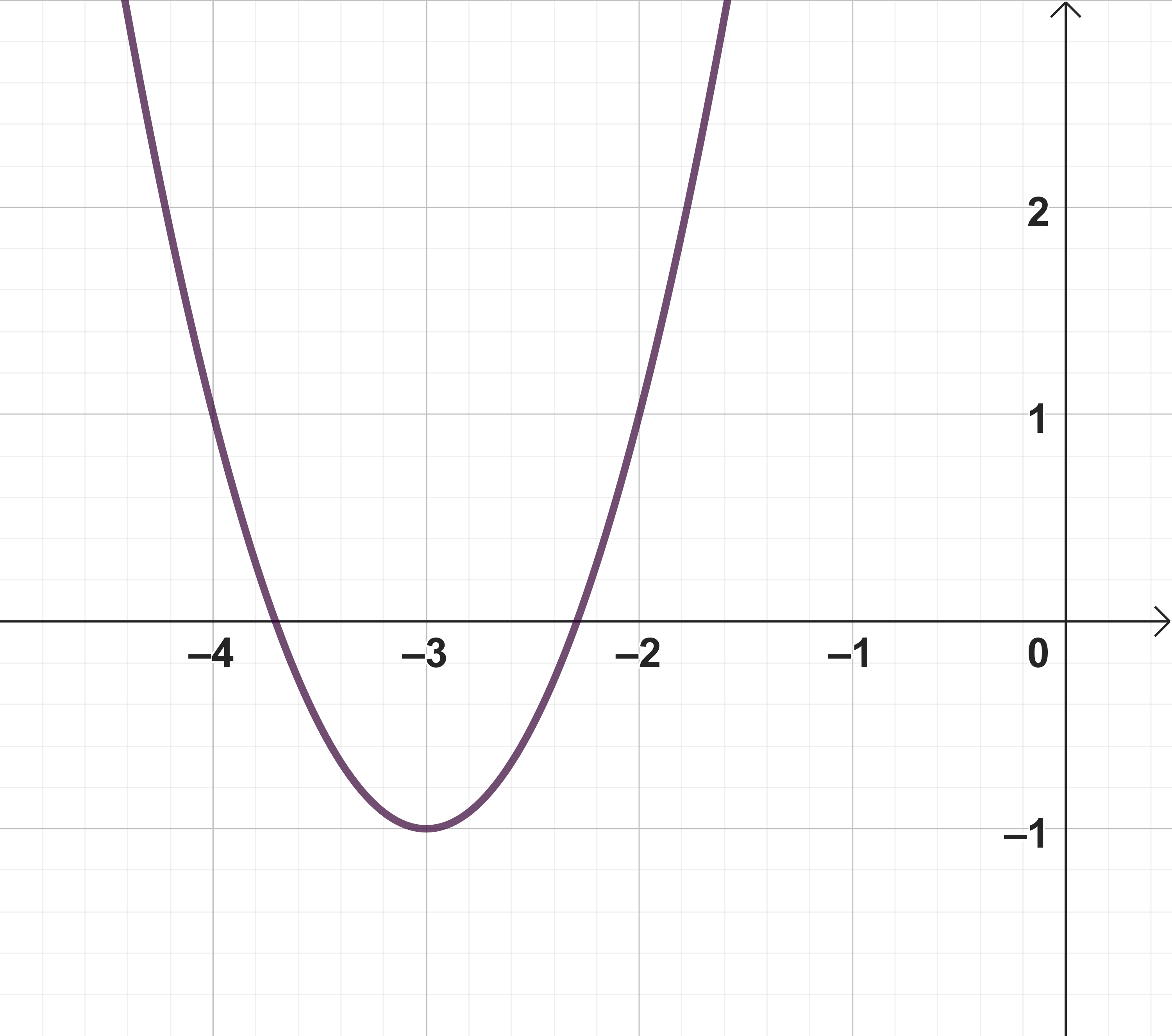
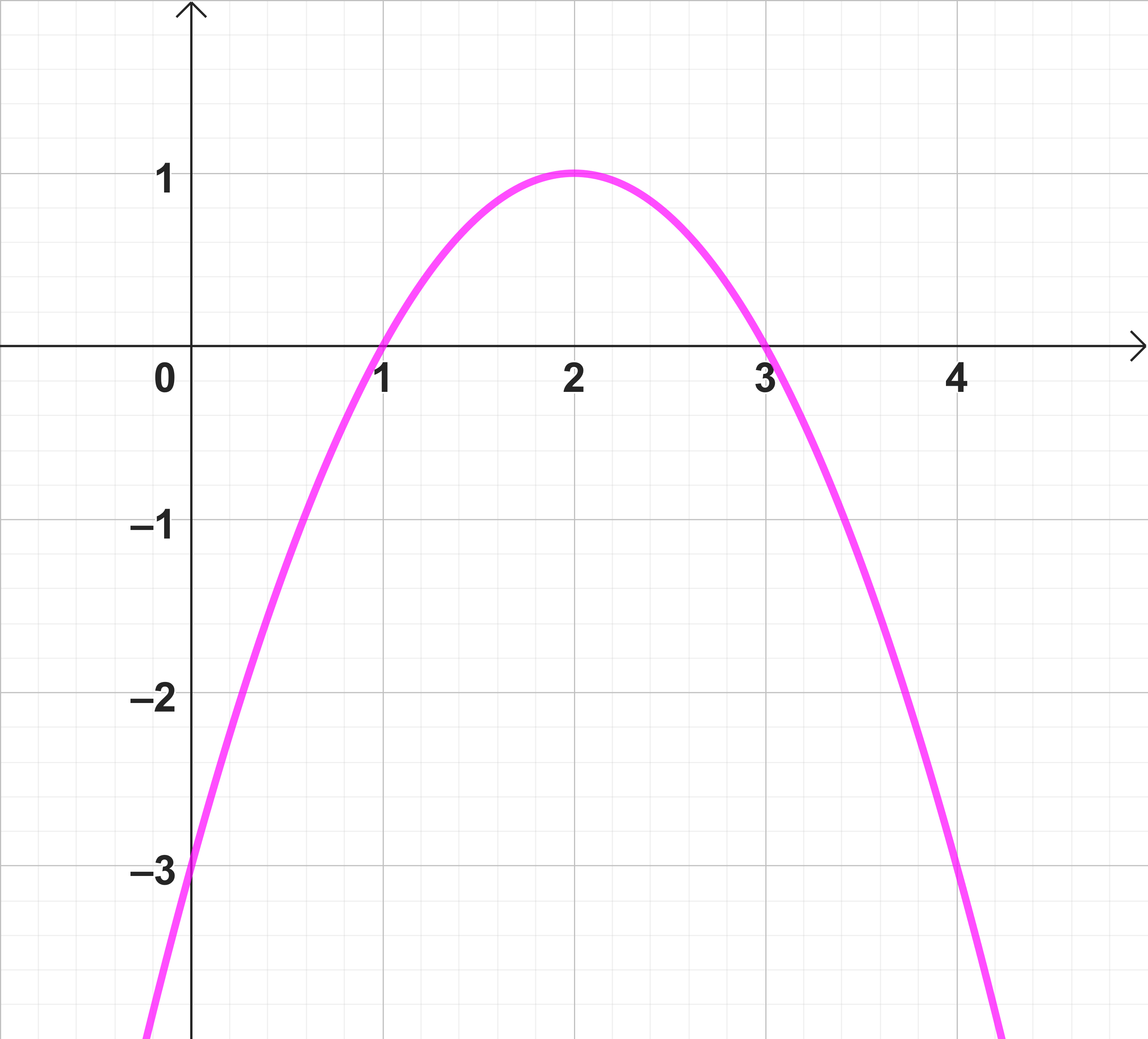
Gib die Scheitelform der Funktionsgleichung der abgebildeten Parabel $f$ an.
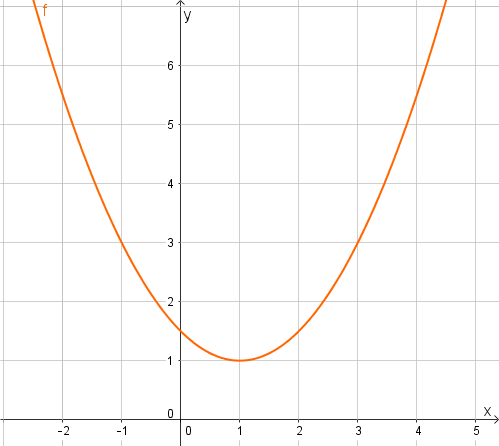
Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel
Die Parabel $f$ hat ihren Scheitel im Punkt $(1 | 1)$ .
Die Funktionsgleichung ist also von der Form $f (x) = a (x - 1)^{2} + 1$ , wobei du $a$ noch zu bestimmen hast.
Wie du anhand der Graphik erkennen kannst, durchläuft $f$ auch den Punkt $(3 | 3)$ . Es gilt also:
$f (3)$ $=$ $3$
↓
Setze die Abbildungsvorschrift von $f$ ein.
$a (3 - 1)^{2} + 1$ $=$ $3$
↓
Vereinfache
$a \cdot 2^{2} + 1$ $=$ $3$ $- 1$
$4 a$ $=$ $2$ $: 4$
$a$ $=$ $0,5$
Somit ist $f (x) = 0,5 (x - 1)^{2} + 1$ .
10
Berechne den Scheitelpunkt folgender Funktionen mithilfe der Formel.
Gib den Scheitelpunkt nach folgendem Muster an: S(a;b) oder S(a|b), also zum Beispiel S(1,2;3) oder S(1,2|3).
1. $f (x) = x^{2} + 6 x + 9$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  $f (x) = x^{2} + 6 x + 9$
  Die Funktion befindet sich bereits in der allgemeinen Form, sodass man die Koeffizienten $a$ , $b$ und $c$ direkt ablesen kann.
  $a = 1, b = 6, c = 9$
  Nun kann man diese in die Formel
  $S = (- \frac{b}{2 \cdot a} | c - \frac{b^{2}}{4 a})$
  einsetzen.
  $S = (- \frac{6}{2 \cdot 1} | 9 - \frac{6^{2}}{4 \cdot 1})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S = (- 3 | 0)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $f (x) = x^{2} - 6 x + 10$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = x^{2} - 6 x + 10$
  Die Funktion befindet sich bereits in der allgemeinen Form, sodass man die Koeffizienten a,b und c direkt ablesen kann.
  $a = 1, b = - 6, c = 10$
  Nun kannst du diese in die Formel
  $S = (- \frac{b}{2 \cdot a} | c - \frac{b^{2}}{4 a})$
  einsetzen.
  $S = (- \frac{(- 6)}{2 \cdot 1} | 10 - \frac{(- 6)^{2}}{4 \cdot 1})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S = (3 | 1)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $f (x) = 2 x^{2} + x - 3$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = 2 x^{2} + x - 3$
  Die Funktion befindet sich bereits in der allgemeinen Form, sodass man die Koeffizienten $a$ , $b$ und $c$ direkt ablesen kann.
  $a = 2, b = 1, c = - 3$
  Nun kann man diese in die Formel
  $S = (- \frac{b}{2 \cdot a} | c - \frac{b^{2}}{4 a})$
  einsetzen.
  $S = (- \frac{1}{2 \cdot 2} | - 3 - \frac{1^{2}}{4 \cdot 2})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S = (- \frac{1}{4} | - \frac{25}{8})$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $f (x) = 3 x^{2} - 12 x + 15$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = 3 x^{2} - 12 x + 15$
  Die Funktion liegt bereits in der allgemeinen Form vor, sodass du die Koeffizienten $a$ , $b$ und $c$ direkt ablesen kannst.
  $a = 3, b = - 12, c = 15$
  Setze $a$ , $b$ , $c$ in die Formel ein.
  $S = (- \frac{(- 12)}{2 \cdot 3} | 15 - \frac{(- 12)^{2}}{4 \cdot 3})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S = (2 | 3)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
5. $f (x) = 16 x^{2} - 8 x + 2$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = 16 x^{2} - 8 x + 2$
  Die Funktion ist bereits in allgemeiner Form gegeben, sodass du die Koeffizienten a,b und c direkt ablesen kannst.
  $a = 16, b = - 8, c = 2$
  Diese setzt du in die Formel
  $S = (- \frac{b}{2 \cdot a} | - \frac{b^{2}}{4 a})$
  ein.
  $S = (- \frac{- 8}{2 \cdot 16} | 2 - \frac{(- 8)^{2}}{4 \cdot 16})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S = (\frac{1}{4} | 1)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6. $f (x) = - 6 x^{2} - 24 x - 29$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = - 6 x^{2} - 24 x - 29$
  Die Funktion befindet sich bereits in der allgemeinen Form, sodass man die Koeffizienten $a$ , $b$ und $c$ direkt ablesen kann:
  $a = - 6, b = - 24, c = - 29$
  Nun kann man diese in die Formel
  $S = (- \frac{b}{2 \cdot a} | c - \frac{b^{2}}{4 a})$
  einsetzen.
  $S = (- \frac{- 24}{2 \cdot (- 6)} | - 29 - \frac{(- 24)^{2}}{4 \cdot (- 6)})$
  Fasse zusammen, indem du die Brüche kürzt und subtrahierst.
  $\Rightarrow S = (- 2 | - 5)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
7. $f (x) = 2 (x^{2} - 4 x + 5)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = 2 (x^{2} - 4 x + 5)$
  Multipliziere aus.
  $= 2 x^{2} - 8 x + 10$
  Bestimme $a$ , $b$ , $c$ aus der allgemeinen Form.
  $a = 2$ , $b = - 8$ , $c = 10$
  Setze $a$ , $b$ , $c$ in die Formel ein.
  $S = (- \frac{(- 8)}{2 \cdot 2} | 10 - \frac{(- 8)^{2}}{4 \cdot 2})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S = (2 | 2)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
8. $f (x) = x (x - 2) + 6$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = x (x - 2) + 6$
  Ausmultiplizieren
  $= x^{2} - 2 x + 6$
  Bestimme $a$ , $b$ , $c$ aus der allgemeinen Form.
  $a = 1$ , $b = - 2$ , $c = 6$
  Setze $a$ , $b$ , $c$ in die Formel ein.
  $S = (- \frac{(- 2)}{2 \cdot 1} | 6 - \frac{(- 2)^{2}}{4 \cdot 1})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S (1 | 5)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
9. $f (x) = x^{2} + \frac{1}{9} (6 x - 26)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = x^{2} + \frac{1}{9} (6 x - 26)$
  Multipliziere aus und fasse zusammen.
  $= x^{2} + \frac{2}{3} x - \frac{26}{9}$
  Bestimme $a$ , $b$ , $c$ aus der allgemeinen Form.
  $a = 1$ , $b = \frac{2}{3}$ , $c = - \frac{26}{9}$
  Setze $a$ , $b$ , $c$ in die Formel ein.
  $S = (- \frac{\frac{2}{3}}{2 \cdot 1} | - \frac{26}{9} - \frac{{(\frac{2}{3})}^{2}}{4 \cdot 1})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S = (- \frac{1}{3} | - 3)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
10. $f (x) = (x - 2) (x + 2)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt einer Funktion
  Gegeben:
  $f (x) = (x - 2) (x + 2)$
  Multipliziere aus und fasse zusammen.
  $= x^{2} - 4$
  Bestimme $a$ , $b$ , $c$ aus der allgemeinen Form.
  $a = 1$ , $b = 0$ , $c = - 4$
  Setze $a$ , $b$ , $c$ in die Formel ein.
  $S = (- \frac{0}{2 \cdot 1} | - 4 - \frac{0^{2}}{(- 4) \cdot 1})$
  Fasse die Terme zusammen, indem du Brüche kürzt und subtrahierst.
  $\Rightarrow S = (0 | - 4)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
11
Scheitelpunktform von Parabeln

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelform
Richtige Lösung
$y = 2 (x - 2)^{2} + 1$
$y = - (x - 2)^{2} + 1$
$y = (x + 2)^{2} + 3$
$y = (x - 3)^{2}$
$y = - (x + 3)^{2} - 1$
$y = 2 (x + 3)^{2} - 1$
12
Die Firma Habmichgern soll eine Brücke planen. Die Länge soll $60 m$ betragen.
Der Chef der Firma bittet dich, mithilfe der folgenden Funktionsgleichung die maximale Höhe der Brücke zu berechnen.
$f (x) = - 0,02 \cdot x^{2} + 1,2 \cdot x$
m

Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertbestimmung durch quadratische Ergänzung
Die Idee hinter den Lösungsmethoden ist, dass der Scheitelpunkt $S$ der höchste Punkt einer nach unten geöffneten Parabel ist. Dass dies eine nach unten geöffnete Parabel ist, lässt sich an dem negativen Koeffizienten $(- 0,02)$ erkennen. Du lernst hier zwei Wege, um an diesen Punkt zu kommen.
1. Lösungsmethode
Scheitelpunkt herausfinden
Der Ansatz dieses Lösungsweges ist es, die Funktion in die Scheitelpunktsform umzuformen.
Die Scheitelpunktsform lautet: $f (x) = a (x - d)^{2} + e$ .
$f (x) = - 0,02 x^{2} + 1,2 x$
Du kannst zunächst $- 0,02$ ausklammern. Dies ist dein $a$ .
$f (x) = - 0,02 \cdot (x^{2} - 60 x)$
Du kannst nun den Wert für $d$ bestimmen, indem du die zweite binomische Formel anwendest.
Multipliziere $(x - d)^{2}$ in der Scheitelpunktsform aus.
Du erhältst:
Du kannst dir nun mithilfe von quadratischer Ergänzung den Term zu einer binomischen Formel konstruieren.
Quadratische Ergänzung:
$x^{2} - 60 x$ ist der erste Teil deiner binomischen Formel, also $x^{2} - 2 d x$ . Demnach ist $d = \frac{60}{2} = 30$ .
Jetzt kannst du deine binomische Formel vervollständigen:
Doch damit du den Wert des Funktionsterms nicht verfälschst, musst du $30^{2}$ auch wieder abziehen.
Der vollständige Term lautet:
Setze den Term in den Funktionsterm ein:
$f (x) = - 0,02 \cdot ((x - 30)^{2} - 30^{2})$
$f (x) = - 0,02 \cdot ((x - 30)^{2} - 900)$
Multipliziere die Klammer aus.
$f (x) = - 0,02 \cdot (x - 30)^{2} + 18$
Lösung
Nun hast du die Scheitelpunktform, an dieser kannst du den Scheitelpunkt ablesen.
Die $y$ -Koordinate ist die Höhe des Brückenbogens, da der Scheitelpunkt der höchste Punkt der Parabel ist.
Also gilt: $h = 18 m$ .
2. Lösungmethode
Ausnutzen der Achsensymmetrie
Der Brückenbogen $f (x)$ ist an einer Senkrechte $t$ durch den Scheitelpunkt $S (x | y)$ achsensymmetrisch. Das kannst du ausnutzen.
Dafür musst du zuerst die $x$ -Koordinate des Scheitelpunkts herausfinden. Wenn du die hast, kannst du auch die $y$ -Koordiante ausrechnen.
Finde die $x$ -Koordinate des Scheitelpunkts.
Der Scheitelpunkt befindet sich in der Mitte der $60 m$ langen Brücke. Also rechnest du:
$x = \frac{60}{2} = 30$
$x = \frac{60}{2} = 30$
$\Rightarrow$ $S (30 | y)$
Setze 30 für $x$ in der Funktion $f (x)$ ein.
$f (x) = - 0,02 x^{2} + 1,2 x$
$f (30) = - 0,02 \cdot 30^{2} + 1,2 \cdot 30$
$y = f (30) = - 0,02 \cdot 30^{2} + 1,2 \cdot 30$
Löse die Funktion nach $y$ auf.
$y = - 0,02 \cdot 30^{2} + 1,2 \cdot 30$
$y = - 18 + 36$
$y = 18$
Nun kannst du $y$ in $S$ einsetzen.
$S (30 | y)$
$\Rightarrow S (30 | 18)$
Lösung
$S (30 | 18)$
Die $y$ -Koordinate des Scheitelpunkts $S$ ist die maximale Höhe des Brückenbogens.
Das heißt:
Die Brücke ist an ihrem höchsten Punkt 18 Meter hoch.
13
Scheitelpunkt Memory
Decke die passenden Paare auf. Wie schnell schaffst du es?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Scheitelpunkt
Richtige Lösung
$y = 2 (x - 2)^{2} + 1$
$y = - (x - 2)^{2} + 1$
$y = (x + 2)^{2} + 3$
$y = (x - 3)^{2}$
$y = - (x + 3)^{2} - 1$
$y = 2 (x + 3)^{2} + 1$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$f (x)$	$=$	$x^{2} + 2 x - 3$
	↓	Ergänze die Funktion quadratisch.
	$=$	$x^{2} + 2 x + 1 - 1 - 3$
	↓	Benutze die 1. binomische Formel.
	$=$	${(x + 1)}^{2} - 4$

$f (x)$	$=$	${(3 - x)}^{2}$
	↓	Klammere (-1) aus.
	$=$	${((- 1) (x - 3))}^{2}$
	↓	Quadriere die einzelnen Faktoren.
	$=$	${(x - 3)}^{2}$

$f (x)$	$=$	$2 ({(x + 1,5)}^{2} + 1)$
	$=$	$2 {(x + 1,5)}^{2} + 2$

$f (x)$	$=$	$2 x^{2} - 4,8 x + 0,88$
	↓	Klammere $2$ vor den $x$ -Termen aus.
	$=$	$2 (x^{2} - 2,4 x) + 0,88$
	↓	Ergänze quadratisch mit ${1,2}^{2}$ .
	$=$	$2 (x^{2} - 2 \cdot 1,2 x + {1,2}^{2} - {1,2}^{2}) + 0,88$
	↓	Multipliziere die Klammer aus.
	$=$	$2 (x^{2} - 2 \cdot 1,2 x + {1,2}^{2}) - 2,88 + 0,88$
	↓	Fasse zusammen.
	$=$	$2 (x^{2} - 2 \cdot 1,2 x + {1,2}^{2}) - 2$
	↓	Fasse zur 2. binomischen Formel zusammen.
	$=$	$2 {(x - 1,2)}^{2} - 2$

$f (x)$	$=$	$(x - 2) (x + 3)$
	↓	Multipliziere aus
	$=$	$x^{2} + x - 6$
	↓	Ergänze quadratisch.
	$=$	$x^{2} + 2 \cdot \frac{1}{2} x + (\frac{1}{2})^{2} - (\frac{1}{2})^{2} - 6$
	↓	Verwende die 1. binomische Formel
	$=$	${(x + 0,5)}^{2} - 6,25$

$f (x)$	$=$	$(x - 2) (x + 3)$
	↓	Multipliziere aus.
	$=$	$x^{2} + x - 6$

$f (x)$	$=$	$x^{2} - 3 x - \frac{3}{4}$
	↓	Ergänze quadratisch.
	$=$	$x^{2} - 2 \cdot 1,5 x + {1,5}^{2} - {1,5}^{2} - \frac{3}{4}$
	↓	Fasse zur 2. binomischen Formel zusammen.
	$=$	${(x - 1,5)}^{2} - 2,25 - \frac{3}{4}$
	↓	Fasse zusammen.
	$=$	${(x - 1,5)}^{2} - 3$
	↓	Lies den Scheitel ab.

$f (x)$	$=$	$- \frac{1}{4} x^{2} + 6 x - 11$
	↓	Klammere aus.
	$=$	$- \frac{1}{4} (x^{2} - 24 x) - 11$
	↓	Ergänze quadratisch.
	$=$	$- \frac{1}{4} (x^{2} \cdot 2 \cdot 12 x + 12^{2} - 12^{2}) - 11$
	↓	Multipliziere die Klammer aus.
	$=$	$- \frac{1}{4} (x^{2} - 2 \cdot 12 x + 12^{2}) + 36 - 11$
	↓	Fasse zusammen.
	$=$	$- \frac{1}{4} (x^{2} - 2 \cdot 12 x + 12^{2}) + 25$
	↓	Fasse zur 2. binomischen Formel zusammen
	$=$	$- \frac{1}{4} {(x - 12)}^{2} + 25$
	↓	Lies den Scheitelpunkt ab.

$f (x)$	$=$	$\frac{1}{2} x^{2} + 4 x - 24$
	↓	Berechne die Nullstellen mit der Mitternachtsformel.
$x$	$=$	$\frac{- 4 \pm \sqrt{16 + 4 \cdot 0,5 \cdot 24}}{2 \cdot 0,5}$
	↓	Der Mittelpunkt der beiden Nullstellen ist der Scheitelpunkt : $\frac{- 12 + 4}{2} = \frac{- 8}{2} = - 4$ .
	$=$	$\frac{- 4 \pm \sqrt{64}}{1}$
	↓	Berechne die y-Koordinate des Scheitelpunktes.
	$=$	$- 4 \pm 8$
$f (- 4)$	$=$	$0,5 \cdot {(- 4)}^{2} + 4 \cdot (- 4) - 24$
	$=$	$- 32$

$f (x)$	$=$	$- 2 x^{2} + 8 x + 10$
	↓	Klammere die $- 2$ aus den ersten beiden Summanden aus.
	$=$	$- 2 (x^{2} - 4 x) + 10$
	↓	Ergänze mit dem Quadrat der Hälfte von $4$ .
	$=$	$- 2 (x^{2} - 4 x + 2^{2} - 2^{2}) + 10$
	↓	Wende die 2. binomische Formel an.
	$=$	$- 2 [{(x - 2)}^{2} - 4] + 10$
	↓	Löse die eckige Klammer auf.
	$=$	$- 2 {(x - 2)}^{2} + 8 + 10$
	↓	Bringe den Term auf Scheitelform.
	$=$	$- 2 {(x - 2)}^{2} + 18$
	↓	Lies den Scheitelpunkt ab.

$\frac{1}{2} x^{2} + 3 x - 4$	$=$	$0$
	↓	Bestimme mithilfe der Mitternachtsformel die Nullstellen dieser Gleichung.
$x_{1}$	$=$	$\frac{- 3 + \sqrt{3^{2} - 4 \cdot 0,5 \cdot (- 4)}}{2 \cdot 0,5}$
	↓	Der Scheitelpunkt liegt genau zwischen den beiden Nullstellen: $x_{s} = \frac{x_{1} + x_{2}}{2} = \frac{- 6}{2} = - 3$ Setzt man diesen $x$ -Wert in die Funktionsgleichung ein, so bekommt man den $y$ -Wert des Scheitelpunktes:
$x_{1}$	$=$	$- 3 + \sqrt{17}$
$x_{2}$	$=$	$\frac{- 3 - \sqrt{3^{2} - 4 \cdot 0,5 \cdot (- 4)}}{2 \cdot 0,5}$
$x_{2}$	$=$	$- 3 - \sqrt{17}$

$f (3)$	$=$	$3$
	↓	Setze die Abbildungsvorschrift von $f$ ein.
$a (3 - 1)^{2} + 1$	$=$	$3$
	↓	Vereinfache
$a \cdot 2^{2} + 1$	$=$	$3$	$- 1$
$4 a$	$=$	$2$	$: 4$
$a$	$=$	$0,5$

$f (x)$	$=$	$3 x^{2} - 4 x + 18$
	↓	Klammere $3$ aus den ersten beiden Summanden aus.
	$=$	$3 (x^{2} - \frac{4}{3} x) + 18$
	↓	Ergänze mit dem Quadrat der Hälfte von $\frac{𝟒}{𝟑}$ .
	$=$	$3 (x^{2} - \frac{4}{3} x + {(\frac{2}{3})}^{2} - {(\frac{2}{3})}^{2}) + 18$
	↓	Wende die 2. binomische Formel an.
	$=$	$3 [{(x - \frac{2}{3})}^{2} - \frac{4}{9}] + 18$
	↓	Löse die eckige Klammer auf.
	$=$	$3 {(x - \frac{2}{3})}^{2} - \frac{4}{3} + 18$
	↓	Bringe den Term auf Scheitelform .
	$=$	$3 {(x - \frac{2}{3})}^{2} + \frac{50}{3}$
	↓	Lies den Scheitelpunkt ab.

$f (x)$	$=$	$- 5 x^{2} - x - 2$
	↓	Klammere $- 5$ aus.
	$=$	$- 5 (x^{2} + \frac{1}{5} x) - 2$
	↓	Ergänze mit dem Quadrat der Hälfte von $\frac{1}{5}$ .
	$=$	$(- 5) \cdot (x^{2} + \frac{1}{5} x + {(\frac{1}{10})}^{2} - {(\frac{1}{10})}^{2}) - 2$
	↓	Fasse zur 1. binomischen Formel zusammen.
	$=$	$- 5 ({(x + \frac{1}{10})}^{2} - {(\frac{1}{10})}^{2}) - 2$
	↓	Multpliziere die Klammer aus.
	$=$	$- 5 {(x + \frac{1}{10})}^{2} + \frac{5}{100} - 2$
	↓	Berechne die rechte Summe.
	$=$	$- 5 {(x + \frac{1}{10})}^{2} - \frac{39}{20}$
	↓	Lies den Scheitelpunkt ab.

$f (x)$	$=$	$2 x + 0,1 x^{2} - 10$
	↓	Sortiere den Ausdruck nach Hochzahlen.
	$=$	$0,1 x^{2} + 2 x - 10$
	↓	Klammere $0,1$ aus den ersten beiden Summanden aus.
	$=$	$0,1 (x^{2} + 20 x) - 10$
	↓	Ergänze mit dem Quadrat der Hälfte von 20.
	$=$	$0,1 (x^{2} + 20 x + 10^{2} - 10^{2}) - 10$
	↓	Wende die 2. binomische Formel an.
	$=$	$0,1 ({(x + 10)}^{2} - 100) - 10$
	↓	Multipliziere die Klammer aus.
	$=$	$0,1 {(x + 10)}^{2} - 10 - 10$
	↓	Bringe den Term auf die Scheitelform.
	$=$	$0,1 {(x + 10)}^{2} - 20$
	↓	Lies den Scheitelpunkt ab.

$f (x)$	$=$	$\frac{2}{3} x^{2} + 8 x$
	↓	Klammere $\frac{2}{3}$ aus.
	$=$	$\frac{2}{3} (x^{2} + 12 x)$
	↓	Ergänze quadratisch.
	$=$	$\frac{2}{3} (x^{2} + 12 x + 6^{2} - 6^{2})$
	↓	Wende die 1. binomische Formel an.
	$=$	$\frac{2}{3} ({(x + 6)}^{2} - 36)$
	↓	Multipliziere die Klammer aus.
	$=$	$\frac{2}{3} {(x + 6)}^{2} - 24$
	↓	$f$ ist nun in Scheitelform. Damit kannst du den Scheitelpunkt ablesen.

$f (x)$	$=$	$\frac{5}{6} x^{2} + x - 1$
	↓	Klammere $\frac{5}{6}$ aus.
	$=$	$\frac{5}{6} (x^{2} + \frac{6}{5} x - \frac{6}{5})$
	↓	Ergänze quadratisch.
	$=$	$\frac{5}{6} \cdot (x^{2} + \frac{6}{5} x + {(\frac{3}{5})}^{2} - {(\frac{3}{5})}^{2} - \frac{6}{5})$
	↓	Wende die 1. binomische Formel an.
	$=$	$\frac{5}{6} \cdot ({(x + \frac{3}{5})}^{2} - \frac{9}{25} - \frac{30}{25})$
	↓	Fasse die negativen Ausdrücke zusammen und multipliziere die Klammer aus.
	$=$	$\frac{5}{6} (x + \frac{3}{5})^{2} - \frac{5}{6} \cdot \frac{39}{25}$
	↓	Zusammenrechnen und kürzen
	$=$	$\frac{5}{6} (x + \frac{3}{5})^{2} - \frac{13}{10}$
	↓	Nun hast du $f$ in Scheitelform vorliegen und kannst daraus den Scheitelpunkt ablesen.

$f (x)$	$=$	$\frac{- 3}{4} x^{2} + x$
	↓	Null setzen.
$0$	$=$	$\frac{- 3}{4} x^{2} + x$
	↓	Klammere $x$ aus.
$0$	$=$	$x (\frac{- 3}{4} x + 1)$
	↓	Eine Nullstelle ist also $x = 0$ . Die zweite Nullstelle erhältst du, indem du $\frac{- 3}{4} x + 1 = 0$ weiter nach $x$ auflöst:
$\frac{- 3}{4} x$	$=$	$- 1$	$\cdot \frac{- 4}{3}$
$x$	$=$	$\frac{3}{4}$
	↓	Der Scheitelpunkt der Parabel liegt genau zwischen den beiden Nullstellen.

Aufgaben zur Berechnung des Scheitelpunktes

Scheitel und Scheitelform

Lösung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

1. Möglichkeit: Lösen anhand der Scheitelform

2. Möglichkeit: Lösen anhand der allgemeinen Form

Hast du eine Frage oder Feedback?

1. Möglichkeit: Lösung anhand der Scheitelform

2. Möglichkeit: Lösung anhand der allgemeinen Form

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

1. Möglichkeit: Lösung anhand der Scheitelform

2. Möglichkeit: Lösung anhand der allgemeinen Form

Hast du eine Frage oder Feedback?

1. Möglichkeit: Lösung anhand der Scheitelform

2. Möglichkeit: Lösung anhand der allgemeinen Form

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Scheitelpunktform von Parabeln

Richtige Lösung

1. Lösungsmethode

Scheitelpunkt herausfinden

Lösung

2. Lösungmethode

Ausnutzen der Achsensymmetrie

Lösung

Scheitelpunkt Memory

Richtige Lösung