Aufgaben zum Verständnis des Grenzwertbegriffs
Kenne deine Grenzen! Vertiefe dein Verständnis zum Grenzwertbegriff mit diesen Übungsaufgaben.
- 1
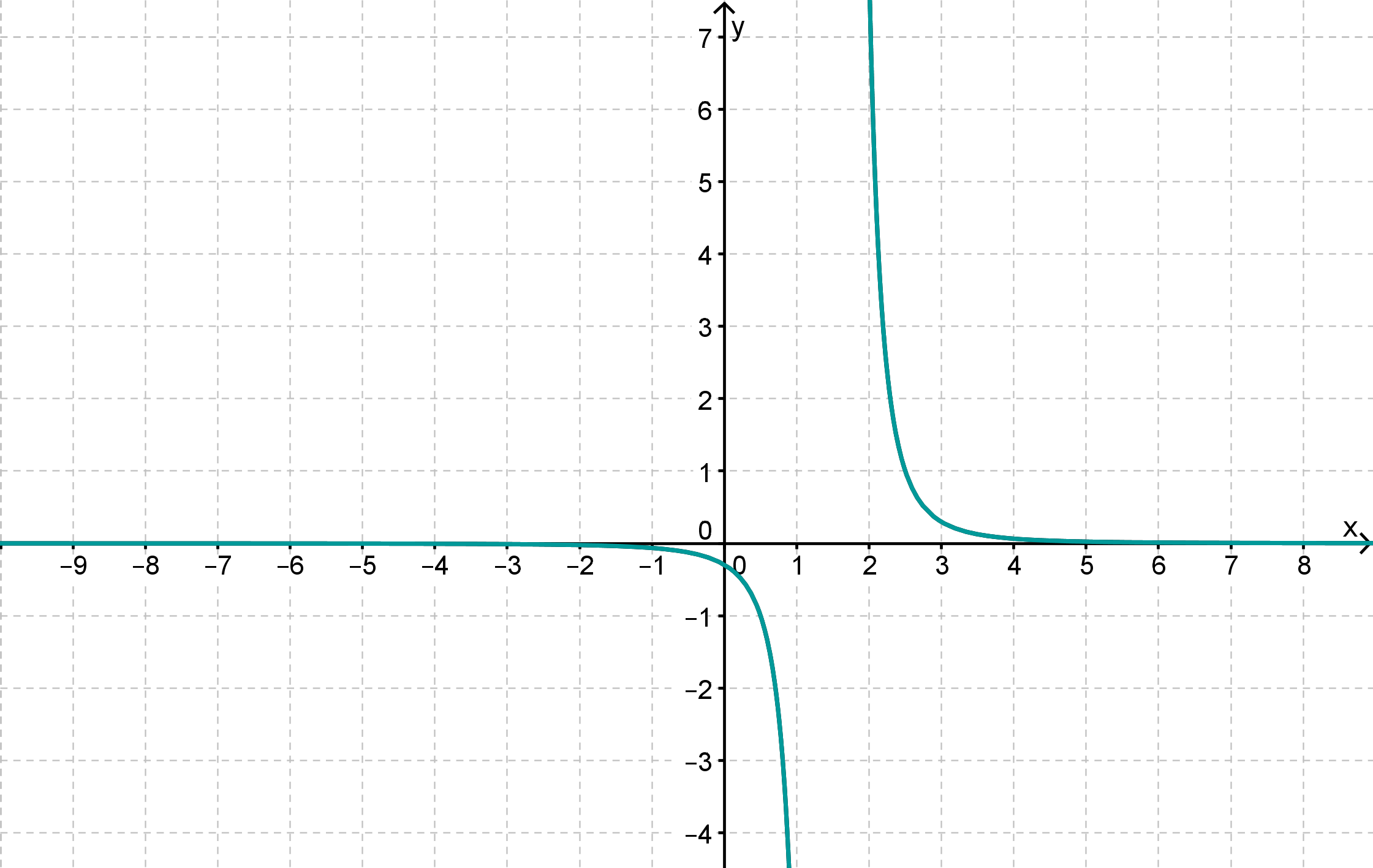
Sieh dir den dargestellten Graphen an: Welchen Wert vermutest du aufgrund der Abbildung für
den Grenzwert für ?
den Grenzwert für ?
den Grenzwert bei Annäherung von links an die Definitionslücke?
den Grenzwert bei Annäherung von rechts an die Definitionslücke?
Bezeichne die Funktion mit und verwende eine korrekte mathematische Schreibweise mit dem Limes (also z. B. bei Teilaufgabe 1 usw.).
(Anmerkung und Hilfe: Die Definitionslücke von ist natürlich bei .)
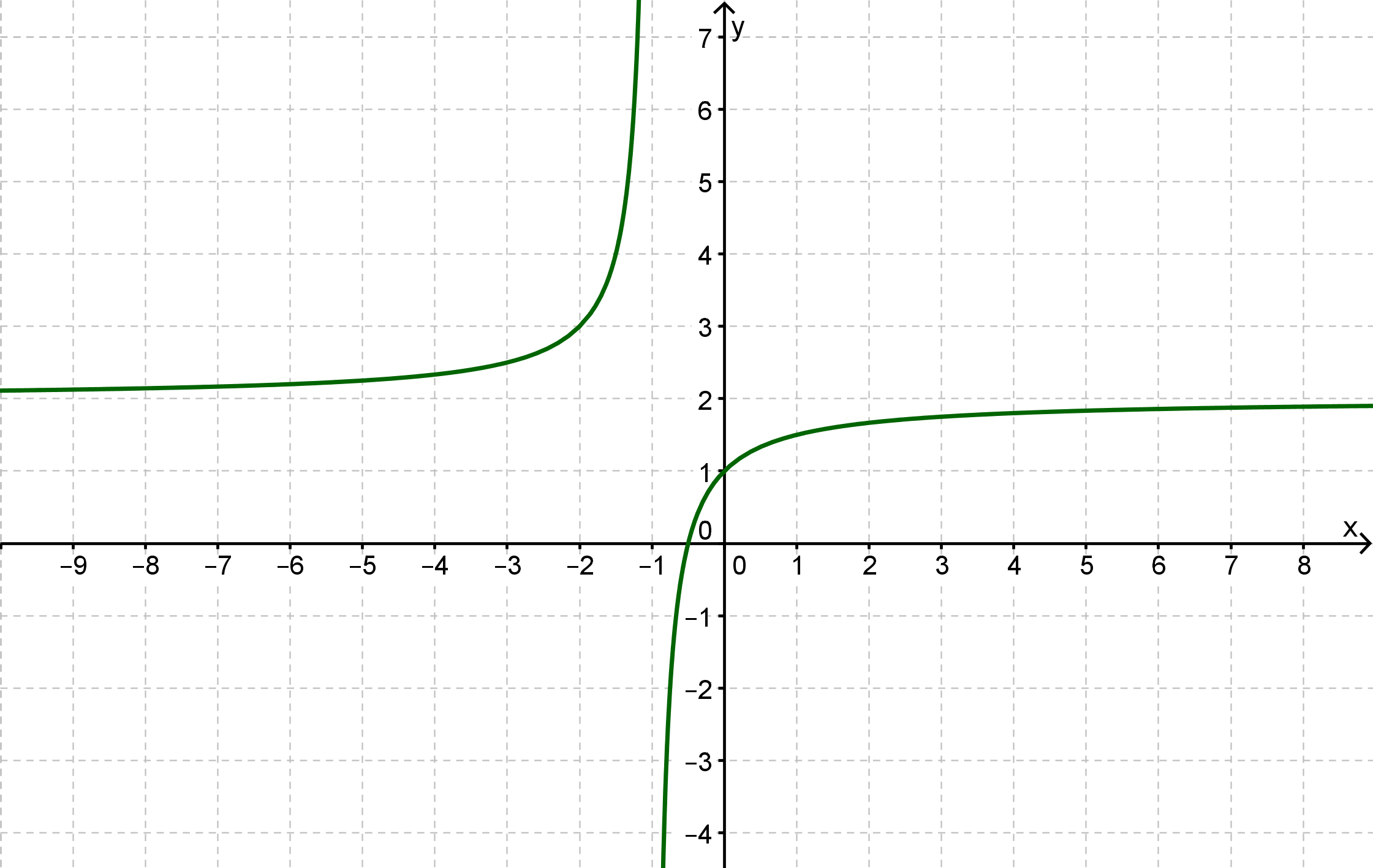
(Anmerkung und Hilfe: Die Definitionslücke von ist natürlich bei .)
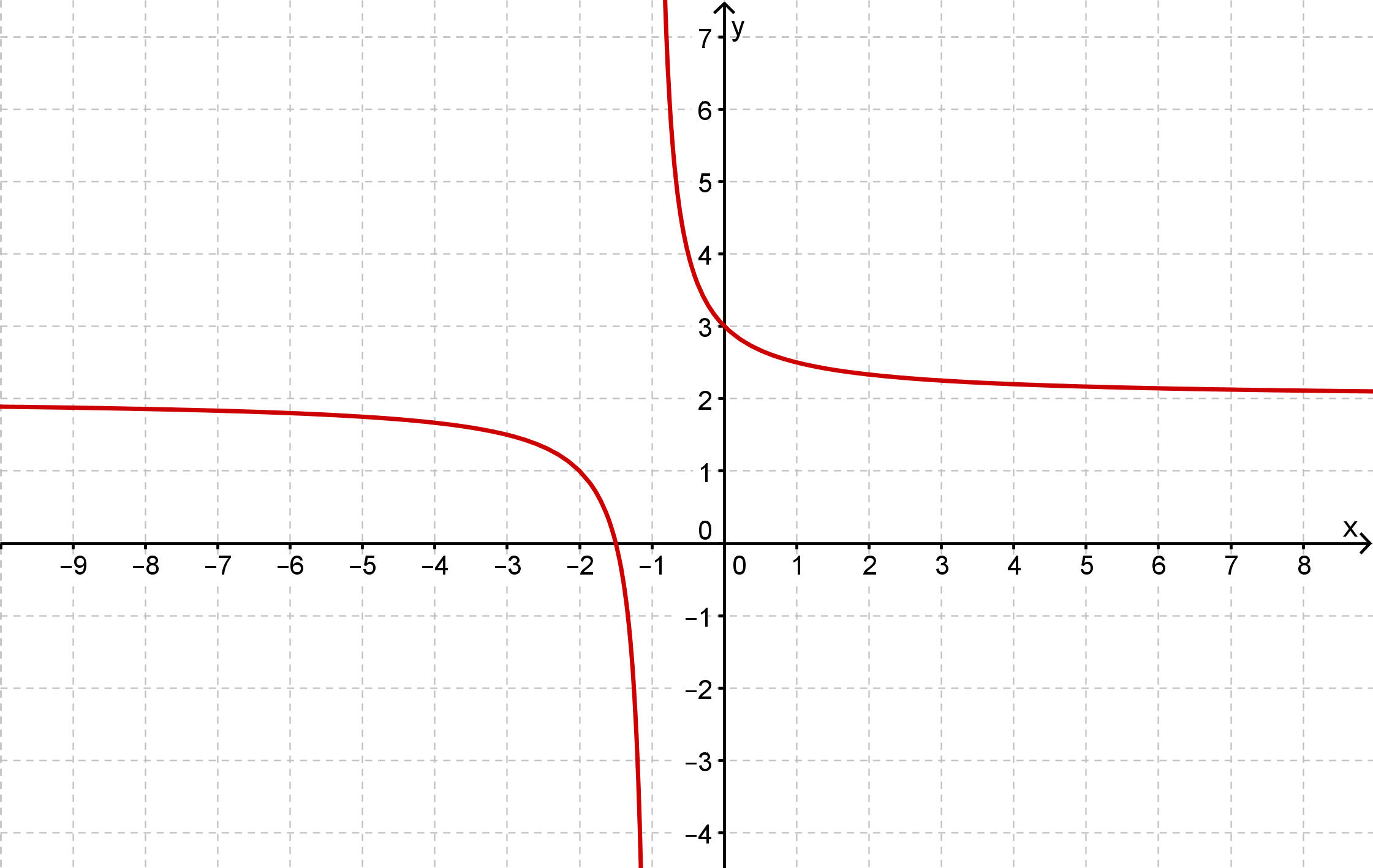
(Anmerkung und Hilfe: Die Definitionslücke von ist bei .)
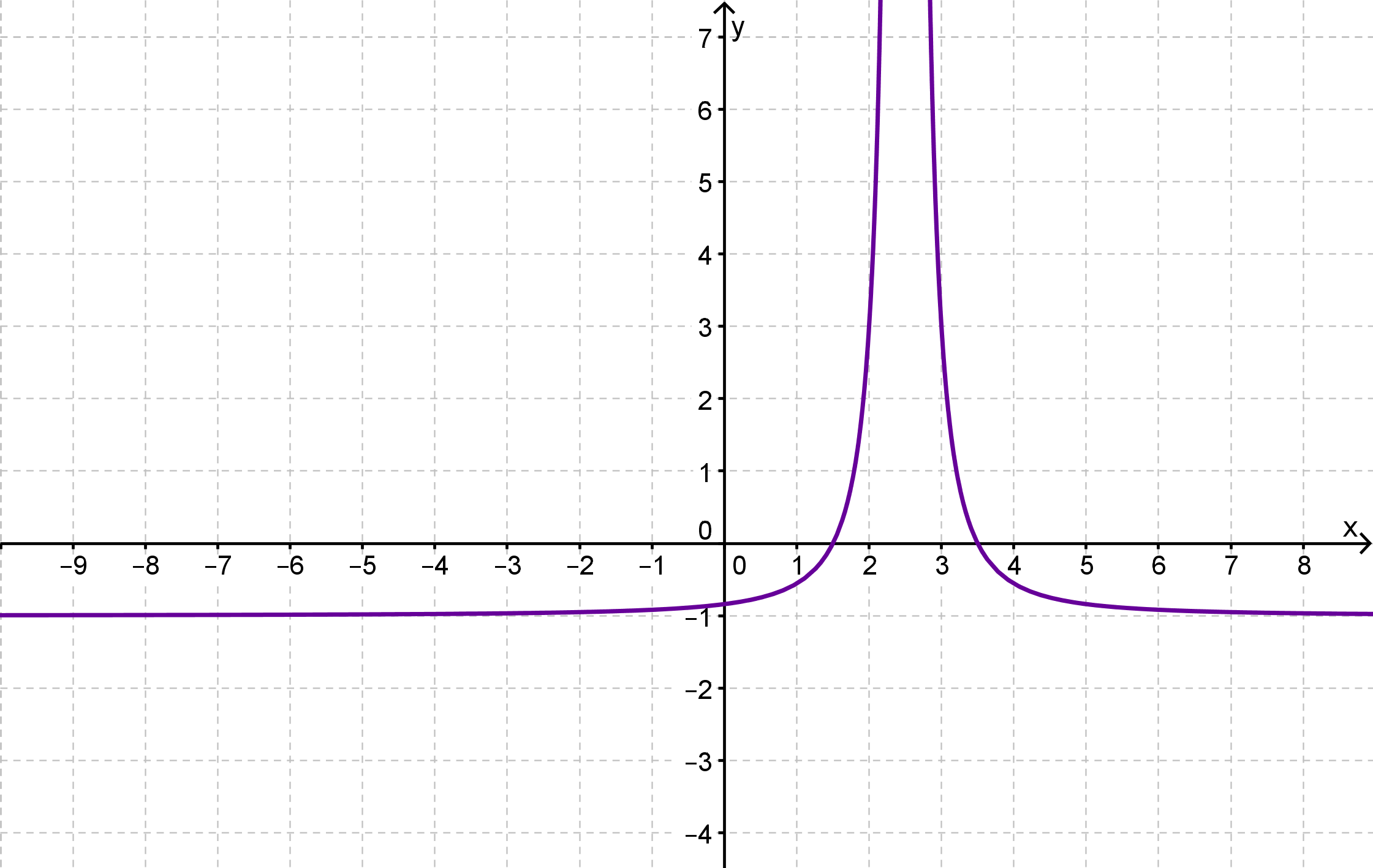
(Anmerkung und Hilfe: Die Definitionslücke von ist natürlich bei .)
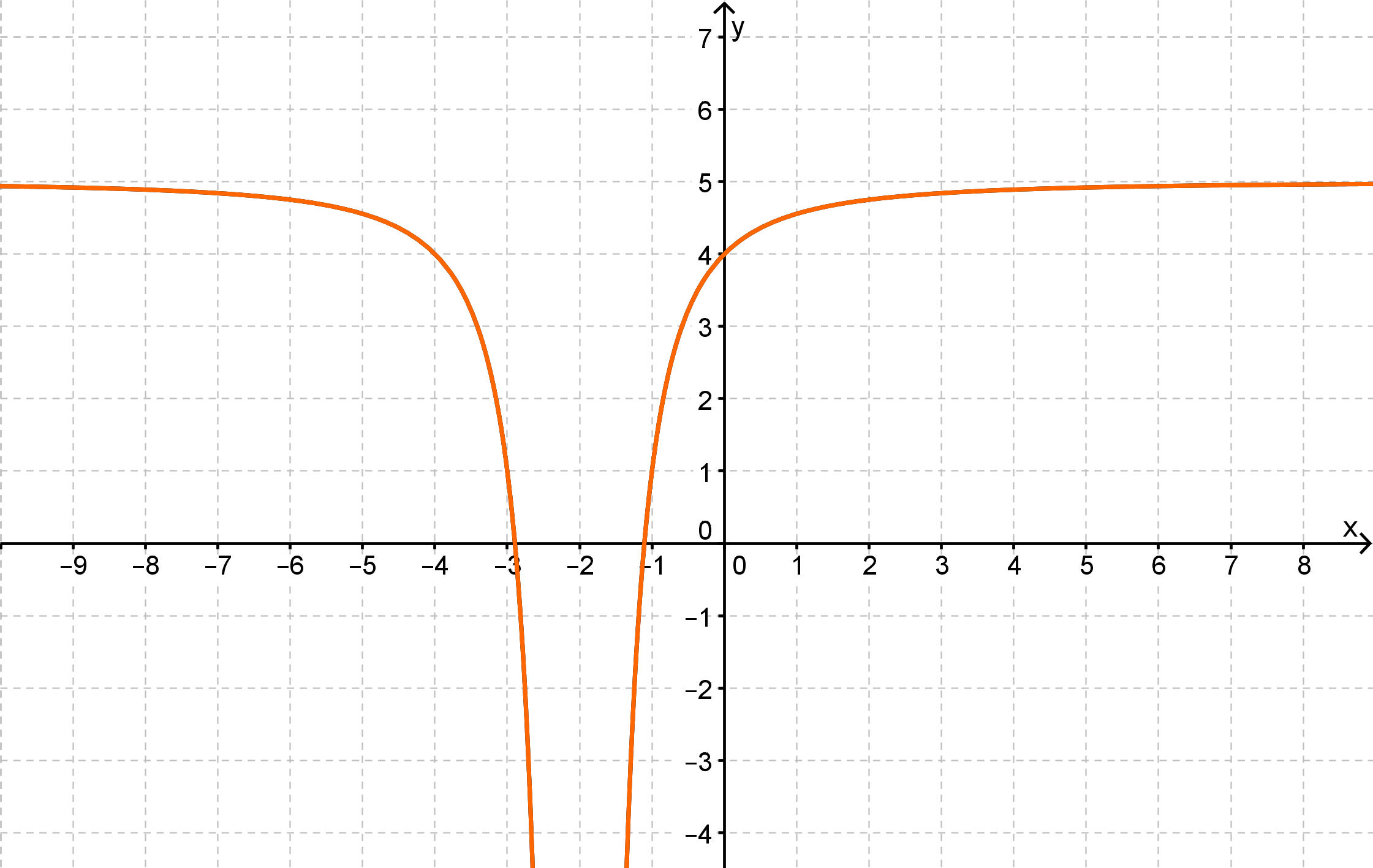
(Anmerkung und Hilfe: Die Definitionslücke von ist bei .)
- 2
Die Graphen haben jeweils keine weiteren Nullstellen oder Extremstellen außer den sichtbaren.
Wähle jeweils die korrekten Grenzwerte, die der Graph für das Verhalten im Unendlichen/ an Asymptoten hat.
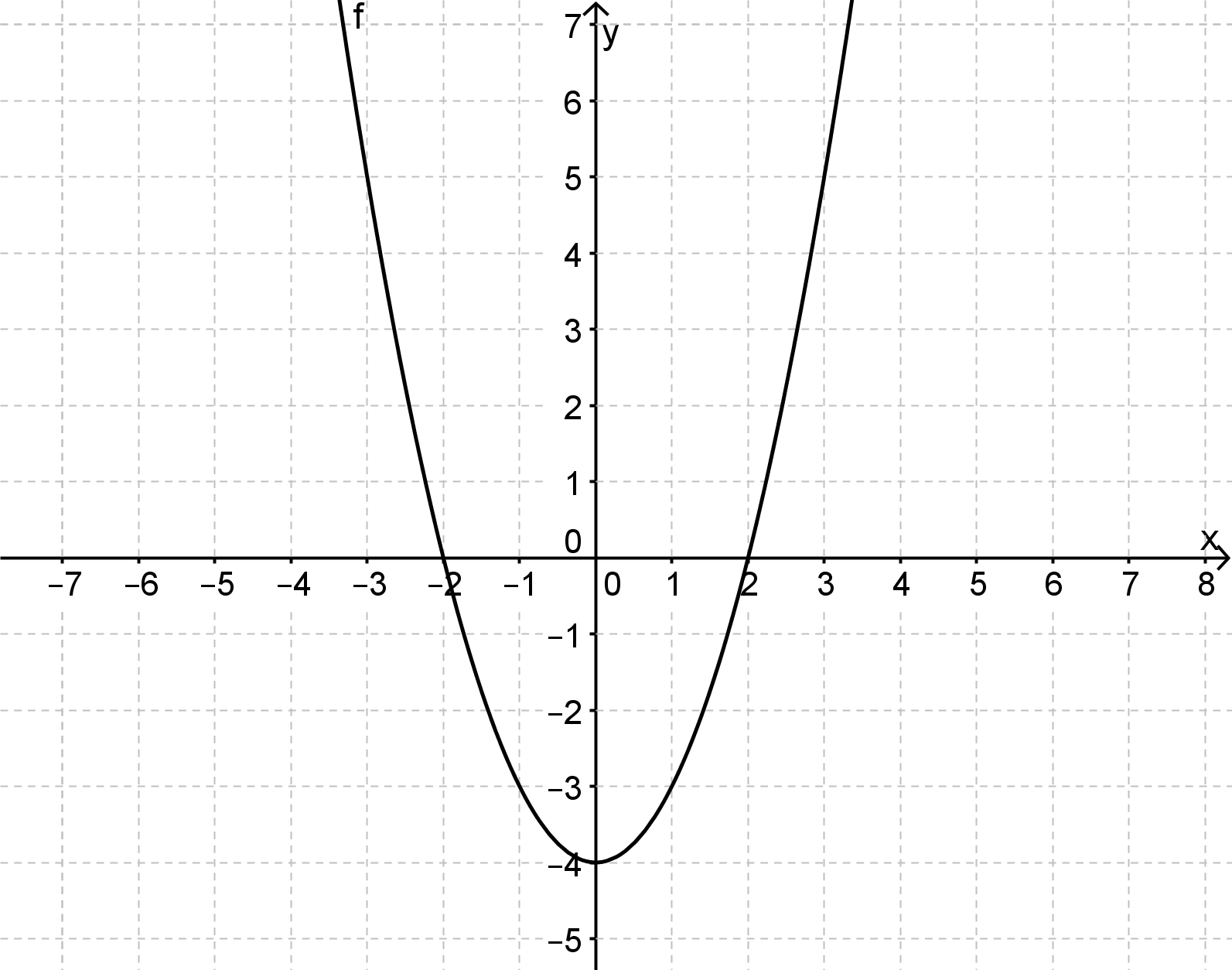
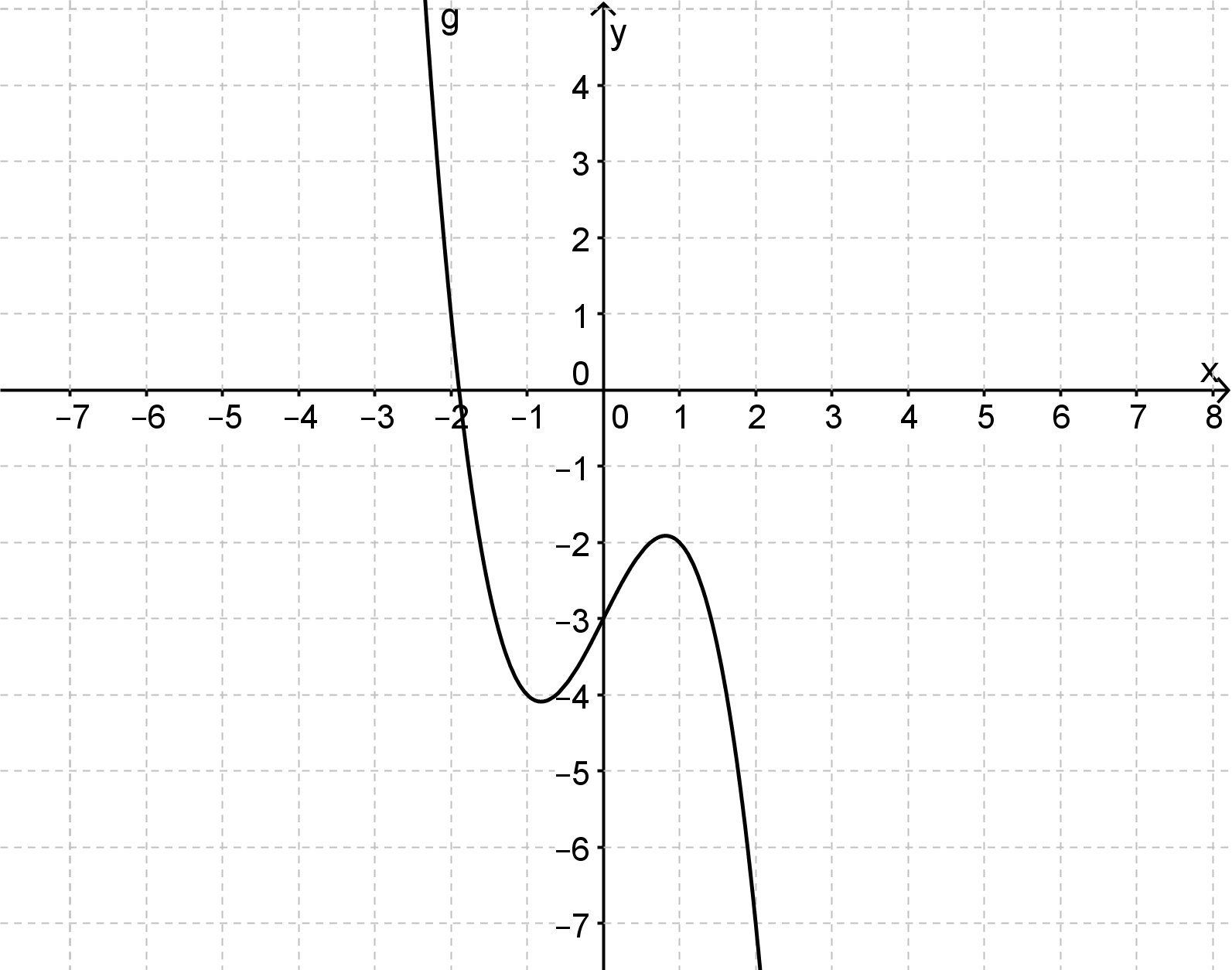
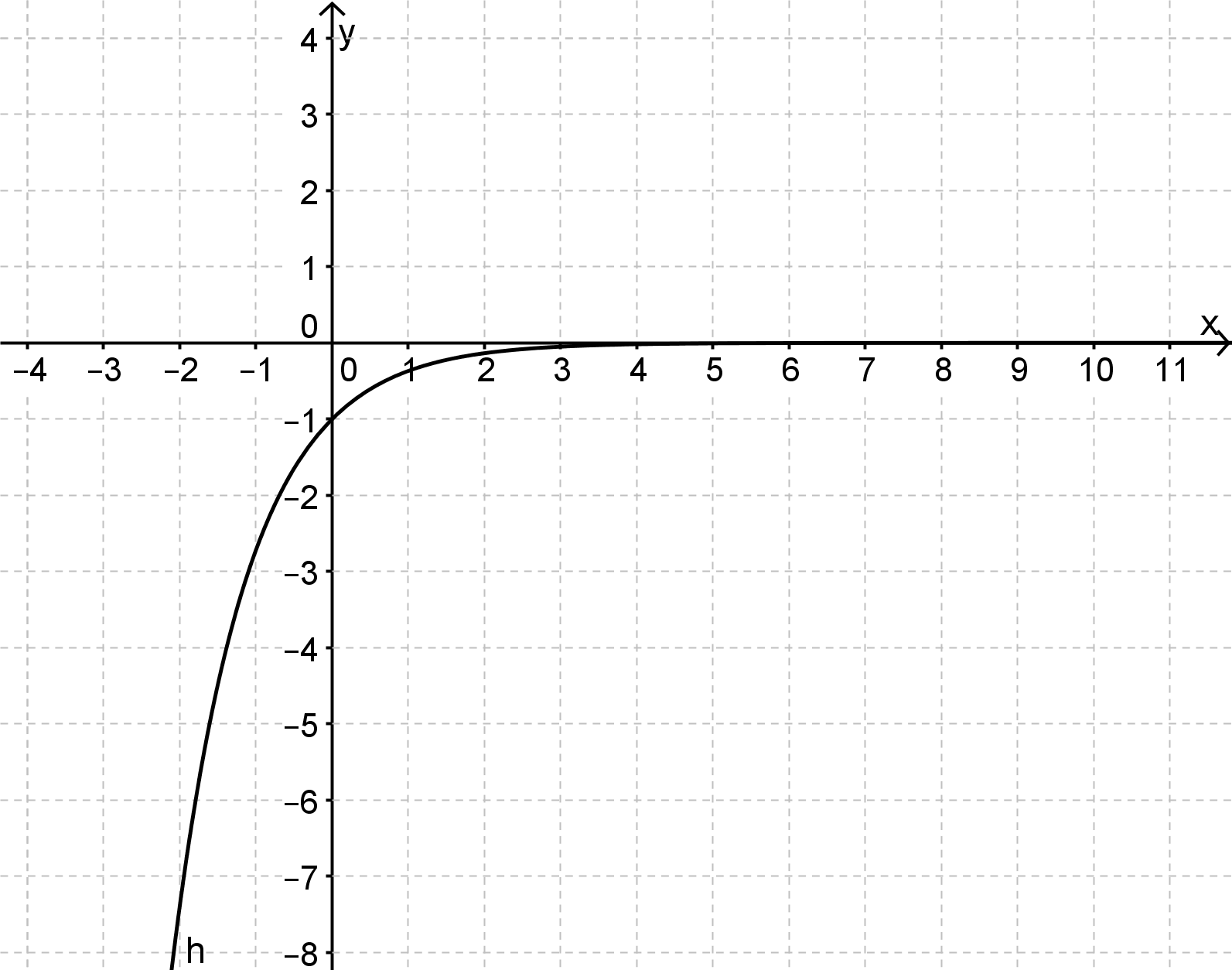
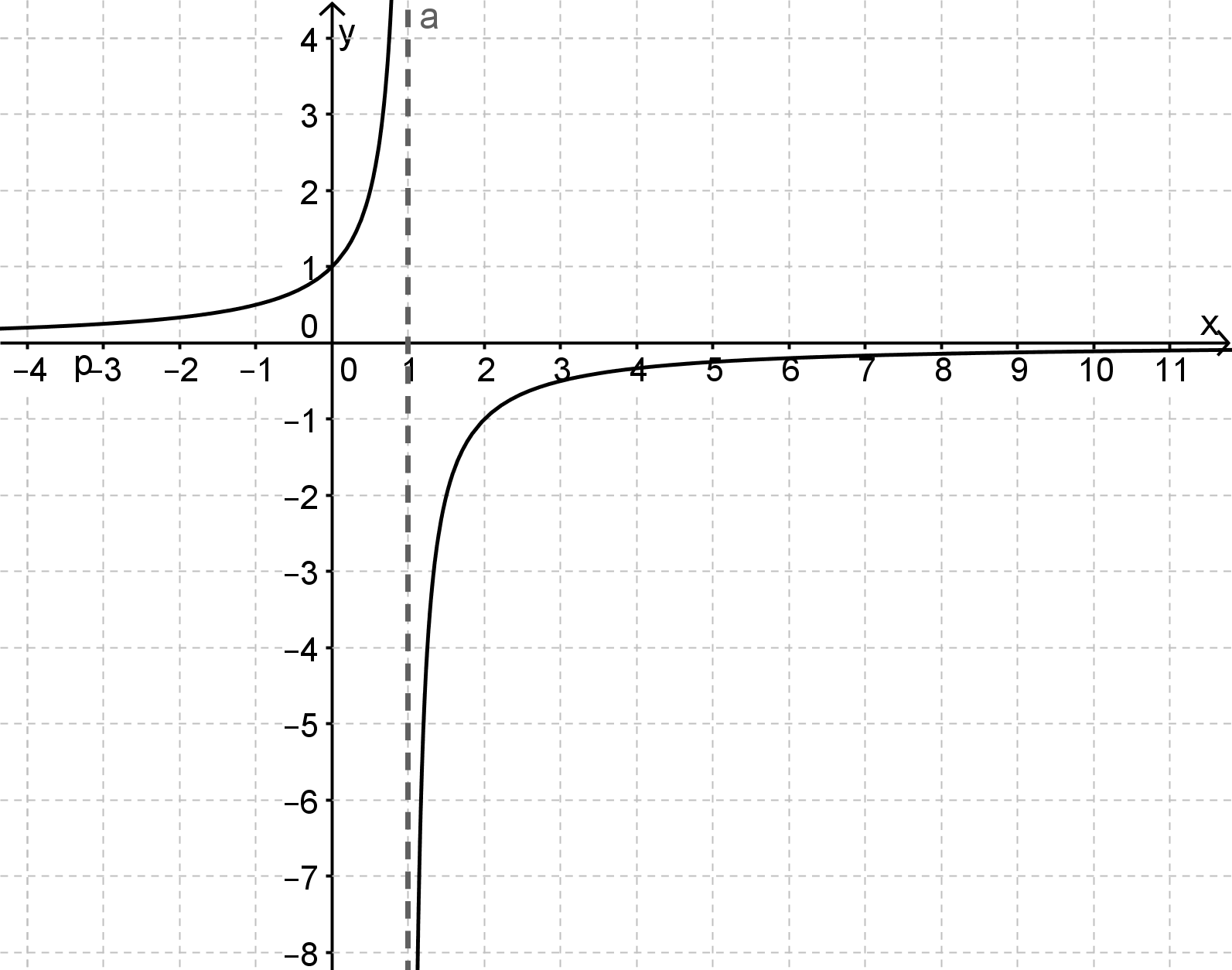
Anmerkung: Bei ist eine senkrechte Asymptote. Der Graph nähert sich dieser an, aber schneidet sie nicht. Auch hier ist der Grenzwert interessant!
Es wird bei den folgenden Antworten nicht der Grenzwert für untersucht, sondern für das Verhalten links von und rechts von
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
