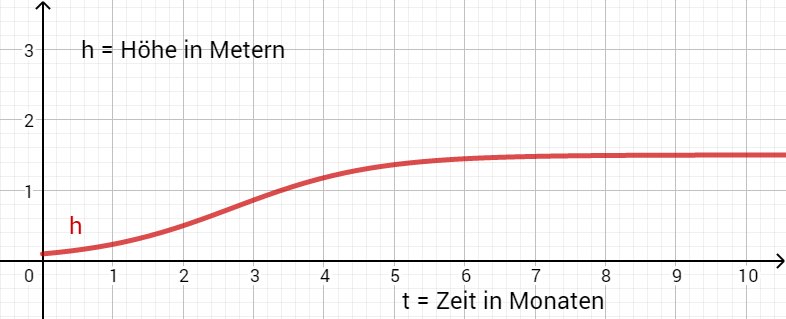
Im Labor wird eine Maispflanze beobachtet, um den Wachstumsverlauf zu erforschen. Dazu beginnen die Forscher ihre Aufzeichnungen mit einem Setzling zum Zeitpunkt t=0 und messen die Höhe der Pflanze kontinuierlich über die nächsten sieben Monate.
Die folgende Funktion konnten die Forscher dabei aufzeichnen:
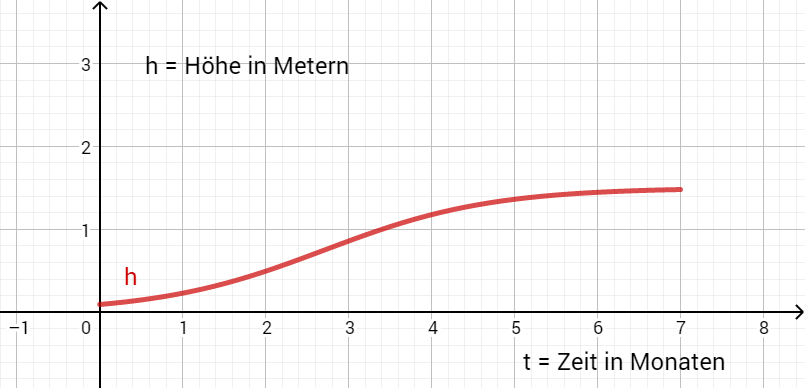
Die Funktion kann modellhaft durch die Funktion beschrieben werden.
Dabei ist die Zeit in Monaten, die seit Beobachtungsbeginn vergangen ist.
ist die Höhe zur Zeit in Metern, die die Maispflanze groß ist.
Berechne die Größe in Zentimeter des Setzlings zu Beginn der Beobachtung!
Berechne, wie viele Zentimeter die Maispflanze in den ersten sechs Wochen nach Aufzeichnungsbeginn gewachsen ist!
Zu welchem Zeitpunkt ist das Wachstum der Pflanze maximal?
Bestimme die Wachstumsrate zu diesem Zeitpunkt in Zentimeter pro Tag!
Bestimme die maximal zu erreichende Höhe dieser Maissorte, indem du den Grenzwert von h(x) gegen Unendlich betrachtest.
Wie müsste die passende Funktionsgleichung aussehen, wenn die Pflanze zu Anfang dieselbe Höhe hätte, also , aber jede weitere Höhe von exakt in der Hälfte der Zeit von erreicht wird ?
Betrachte Teilaufgabe . Begründe, warum die anderen beiden Antworten nicht richtig sein können!
Betrachte Teilaufgabe . Gebe den entsprechenden Wert von an!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?