Assoziativgesetz

Das Assoziativgesetz besagt, dass bei der reinen Addition und bei der reinen Multiplikation mehrerer Zahlen die Klammern beliebig gesetzt werden dürfen. Die Reihenfolge der Berechnung ist also egal.

Beispiele:

$(2 + 3) + 4 = 2 + (3 + 4) = 9$

$(2 \cdot 3) \cdot 4 = 2 \cdot (3 \cdot 4) = 24$

Assoziativgesetz für Addition

Allgemein

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\left(a+b\right)+c\;=\;a+\left(b+c\right)\end{array}

Beispiel

$(2 + 3) + 4 = 5 + 4 = 9$	$2 + (3 + 4) = 2 + 7 = 9$

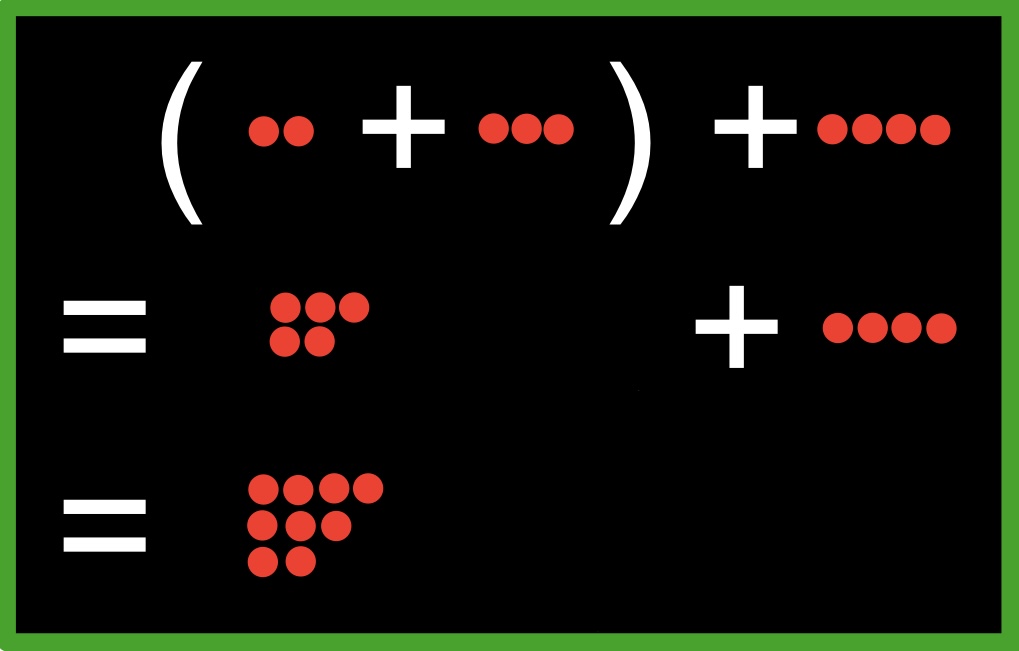Es kommt also das gleiche Ergebnis raus. Das ist die Aussage des Assoziativgesetzes für Addition.

Assoziativgesetz für Multiplikation

Allgemein

\displaystyle \left(a\cdot b\right)\cdot c\;=\;a\cdot\left(b\cdot c\right)

Beispiel

$(2 \cdot 3) \cdot 4 = 6 \cdot 4 = 24$	$2 \cdot (3 \cdot 4) = 6 \cdot 4 = 24$

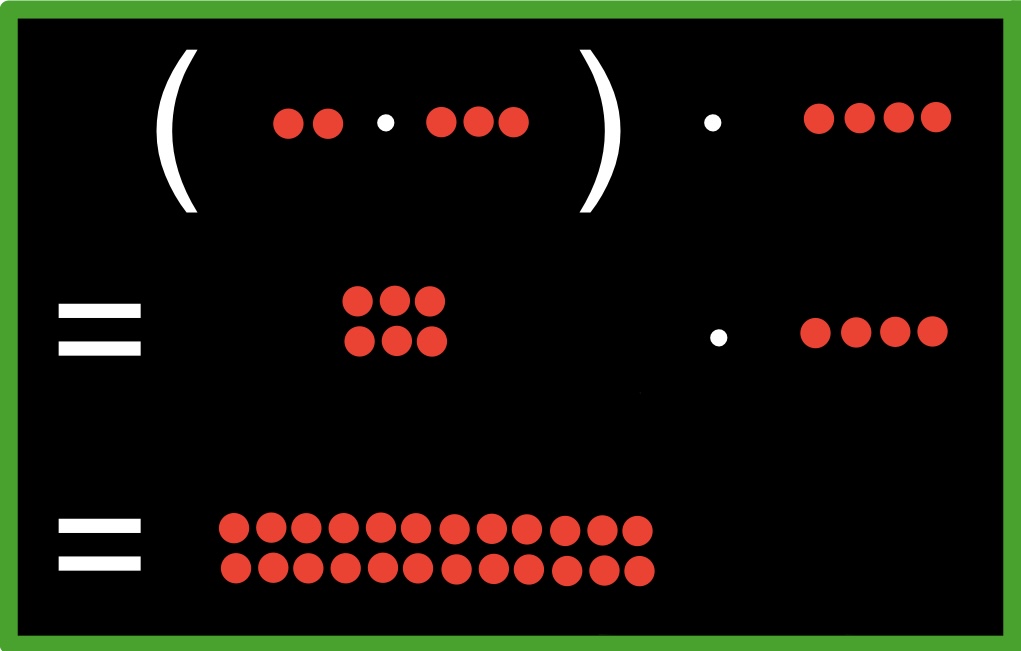Es kommt also das gleiche Ergebnis raus. Das ist die Aussage des Assoziativgesetzes für Multiplikation.

Vorsicht

Das Assoziativgesetz gilt nur bei der reinen Addition und bei der reinen Multiplikation. Wenn Addition und Multiplikation gemischt vorkommen, kann man das Assoziativgesetz nicht anwenden!

Beispiel:

$(2 + 3) \cdot 4 ≠ 2 + (3 \cdot 4) = 24$

Assoziativgesetz erklärt

In diesem Video wird das Assoziativgesetz erklärt und mithilfe von Beispielen vertieft.

Laden

Übungsaufgaben: Assoziativgesetz

Laden

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?