Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Abbildungen im Raum mithilfe von Matrizen (3)

Drehungen

Ein gegebener Punkt EE soll um eine Drehachse gg mit dem Drehwinkel α\alpha gedreht werden.

Wie lautet die zugehörende Drehmatrix, mit der die Koordinaten des gedrehten Punktes E′E' bestimmt werden können?

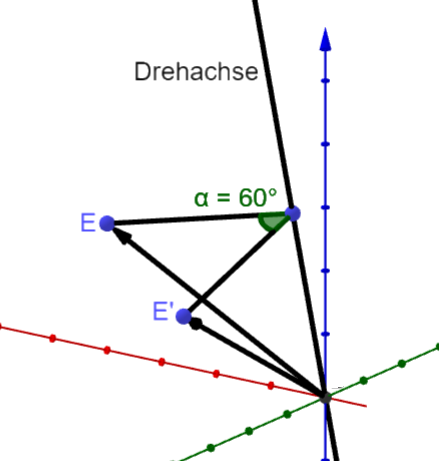
Drehung um 60 Grad um die Drehachse

Drehung um 60 Grad um die Drehachse

Drehung um eine Drehachse gg mit der Drehwinkel α\alpha

Die Matrix DD beschreibt die Drehung um eine Drehachse gg mit dem Drehwinkel α\alpha.

Jeder Punkt der Drehachse gg ist ein Fixpunkt. Weiterhin gilt det⁡(D)=1\det\left(D\right)=1.

Bei der Drehmatrix sind die Spaltenvektoren paarweise orthogonal, d.h. sie stehen senkrecht aufeinander und haben jeweils die Länge 11.

Ist die Drehachse der Einheitsvektor n∘→=(n1n2n3)\overrightarrow{n^\circ}=\begin{pmatrix}n_1\\n_2\\n_3\end{pmatrix}und ist der Drehwinkel α\alpha, dann gehört die folgende Drehmatrix DD zu dieser Abbildung:

MerkeDrehmatrix DD

D=(n12(1−cos⁡α)+cos⁡αn1n2(1−cos⁡α)−n3sin⁡αn1n3(1−cos⁡α)+n2sin⁡αn2n1(1−cos⁡α)+n3sin⁡αn22(1−cos⁡α)+cos⁡αn2n3(1−cos⁡α)−n1sin⁡αn3n1(1−cos⁡α)−v2sin⁡αn3n2(1−cos⁡α)+n1sin⁡αn32(1−cos⁡α)+cos⁡α)\def\arraystretch{1.25} D=\left(\begin{array}{rrrc}n_1^2(1-\cos\alpha)+\cos\alpha&n_1n_2(1-\cos\alpha) -n_3\sin\alpha& n_1n_3(1-\cos\alpha) +n_2\sin\alpha\\n_2n_1(1-\cos\alpha)+n_3\sin\alpha&n_2^2(1-\cos\alpha) +\cos\alpha& n_2n_3(1-\cos\alpha) -n_1\sin\alpha & \\n_3n_1(1-\cos\alpha)-v_2\sin\alpha&n_3n_2(1-\cos\alpha) +n_1\sin\alpha& n_3^2(1-\cos\alpha) +\cos\alpha\end{array}\right)

Drehwinkel α\alpha ist gesucht

Ist die Drehmatrix DD gegeben und ist der Drehwinkel α\alpha gesucht, dann gilt:

cos⁡α=12(Spur(D)−1)\displaystyle \cos\alpha=\dfrac{1}{2}\left(\text{Spur}(D)-1\right)

Dabei ist die Spur der Matrix DD gleich d11+d22+d33d_{11}+d_{22}+d_{33} (Summe der Diagonalelemente).

Spezielle Drehachsen

Drehung um die x1x_1-Achse:

Dx1=(1000cos⁡α−sin⁡α0sin⁡αcos⁡α)\def\arraystretch{1.25} D_{x_1}=\left(\begin{array}{rrrc}1&0&0\\0&\cos\alpha& -\sin\alpha \\0&\sin\alpha & \cos\alpha \end{array}\right)

Drehung um die x2x_2-Achse:

Dx2=(cos⁡α0sin⁡α010−sin⁡α0cos⁡α)\def\arraystretch{1.25} D_{x_2}=\left(\begin{array}{rrrc}\cos\alpha&0&\sin\alpha \\0&1& 0 \\-\sin\alpha&0&\cos\alpha \end{array}\right)

Drehung um die x3x_3-Achse:

Dx3=(cos⁡α−sin⁡α0sin⁡αcos⁡α0001)\def\arraystretch{1.25} D_{x_3}=\left(\begin{array}{rrrc}\cos\alpha&-\sin\alpha&0\\\sin\alpha&\cos\alpha& 0 \\0&0 & 1\end{array}\right)


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?