Zur Erstellung der Inhalte auf Serlo verwenden wir insbesondere in den Bereichen Mathematik und Physik bei der Darstellung von Formeln, Gleichungen und Rechnungen das Textsatzprogramm (gesprochen: Latech).
Diese Hilfeseite soll dir technische Unterstützung bei der Verwendung von bieten.
Wichtig: Auf serlo.org wird nur zum Schreiben von Formeln verwendet, normaler Text soll nicht in geschrieben werden.
Inhaltsverzeichnis
Die -Umgebung im Serlo Editor
Bevor es um die korrekte Darstellung mathematischer Ausdrücke geht, siehst du hier zunächst, wie du die -Umgebung öffnen kannst.
Schritt 1:
Klicke auf das Formelsymbol, welches im Bild mit einem roten Pfeil markiert ist.
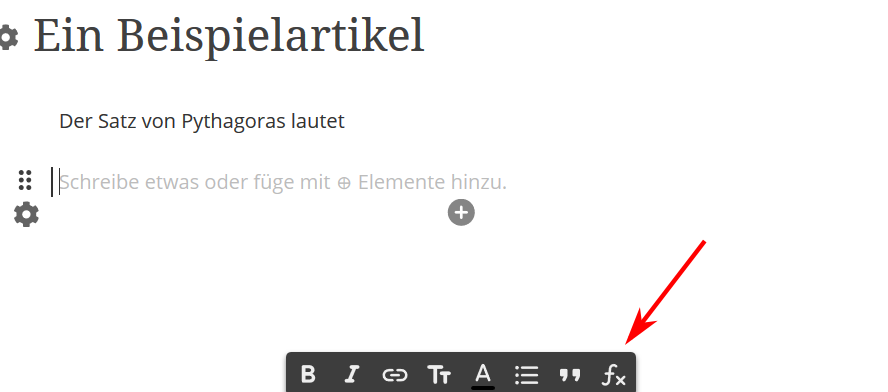
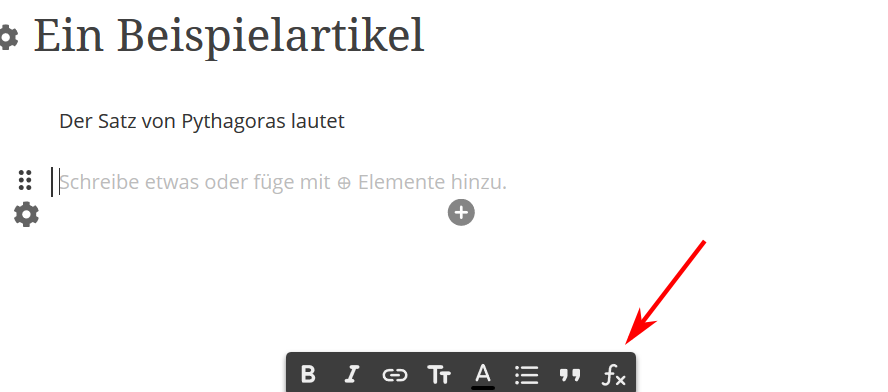
Schritt 2:
Es öffnet sich das in der Abbildung dargestellte Fenster. Wähle nun im Drop-down-Menü die Option latex.
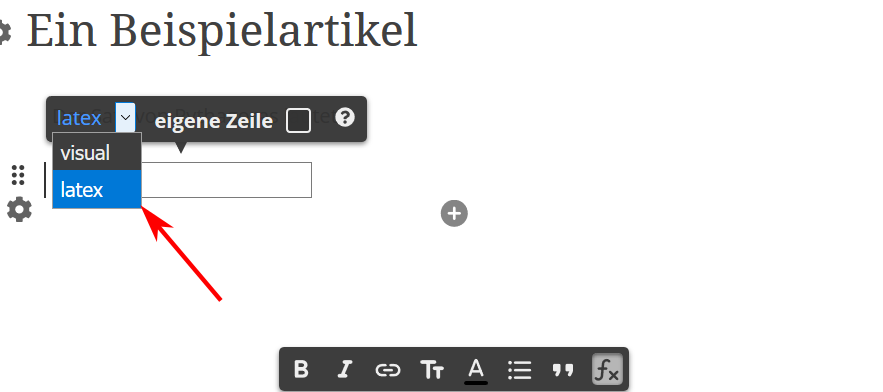
Alle anderen Umgebungen, Funktionen und Symbole, die hier im Folgenden aufgelistet sind, müssen in dieser Umgebung geschrieben sein, um richtig dargestellt zu werden.
Grundlegende mathematische Schreibweisen
Kommazahlen
Kommazahlen: in wird aus der Eingabe 2,14 dies hier: . Wenn man den Abstand hinter dem Komma vermeiden will, schreibt man 2{,}14 und erhält .
Indizes und Exponenten
Indizes werden innerhalb der -Umgebung mit dem Befehl _ erzeugt. Für Exponenten wird ^ verwendet. Enthält der Index beziehungsweise der Exponent mehr als ein Zeichen, so müssen die beiden oben genannten Befehle durch { } erweitert werden. Also _{ } beziehungsweise ^{ }.
Ausgabe | LaTeX-Code | Erklärung |
|---|---|---|
x^2 | Exponenten mit Zirkumflex: ^ | |
x^{2a} | Exponenten mit zwei oder mehr Zeichen in geschweifte Klammern | |
x_1 | Indizes mit Unterstrich: _ | |
x_{1,2} | Indizes mit zwei oder mehr Zeichen in geschweifte Klammern |
Trigonometrische Funktionen
Für die korrekte Schreibweise von trigonometrischen Funktionen ist zu beachten, dass man, statt einfach nur sin(x), den Befehl \sin(x) verwendet.
Diese Regel gilt auch für alle anderen trigonometrischen Funktionen. Hier kannst du eine Tabelle ausklappen, in der du die entsprechenden Befehle findest.
Wurzelausdrücke
Die Darstellung von Wurzelausdrücken gelingt innerhalb der -Umgebung mit dem Befehl \sqrt{ }. Dieser Befehl gibt standardmäßig die Quadratwurzel aus.
Benötigt man allgemeiner die n-te Wurzel, so verwendet man den Befehl \sqrt[ ]{ }.
Ausgabe | LaTeX-Code | Erklärung |
|---|---|---|
\surd | Wurzelsymbol ohne Radikant | |
\sqrt{x} | ||
\sqrt[a]{x} |
Brüche
Für Brüche wird der Befehl \dfrac{ }{ } verwendet. Der Inhalt innerhalb der ersten { } stellt den Zähler des Bruches dar, während der Inhalt in den zweiten { } den Nenner des Bruches darstellt.
Ausgabe | LaTeX-Code | Erklärung |
|---|---|---|
\dfrac{3+x}{2x} | Bei Brüchen Zähler und Nenner in geschweifte Klammern |
Griechisches Alphabet
Text in der -Umgebung
Gelegentlich kommt es vor, dass innerhalb einer -Umgebung neben Formeln und Gleichungen auch Text benötigt wird. Dafür verwendet man den Befehl \text{ }. Der Befehl spielt vor allem in der Physik eine Rolle, da beispielsweise Einheiten durch diesen Befehl korrekt dargestellt werden. Viele Einheiten sind im Abschnitt Serlo-eigene Befehle definiert.
Beispiel: Die Eingabe
a = 3 \ \dfrac{\text{m}}{\text{s}^2}liefert
Farben
Du kannst auch Teile deiner Formel färben, beispielsweise um in einer Rechnung einen wichtigen Schritt zu kennzeichnen. Dies funktioniert mit dem Befehl \textcolor{}{}.
In die erste geschweifte Klammer gibst du den Hex-Code der Farbe ein, die du verwenden möchtest. Beispielsweise hat und Die Hex-Codes für die empfohlenen Farben auf Serlo findest du in der Hilfeseite für Bilder und Grafiken.
In die zweite geschweifte Klammer trägst du den LaTeX-Code ein, den du farbig markieren möchtest.
Ein Beispiel: Der LaTeX-Code
f(x) = \textcolor{ff6600}{1013}\cdot \textcolor{009999}{1,42}^x = \textcolor{ff6600){a}\cdot \textcolor{009999}{b}^xliefert die Ausgabe:
Achte darauf, dass du nicht und in Kombination verwendest, um Elemente voneinander zu unterscheiden - Menschen mit einer Rot-Grün-Schwäche können hier Probleme haben.
Die Hex-Codes der Farben, die du im Text nutzen kannst, sind:
Blau: #1794c1
Grün: #006400
Orange: #ff6600
Klammern und Betragsstriche
Klammern werden immer mit \left und \right geschrieben, damit sie sich an die Größe der Formel dazwischen anpassen können. Eine Auflistung der wichtigsten Klammernotation kannst du unten ausklappen.
Auch Betragsstriche können durch \left und \right gesetzt werden. Die Eingabe
f(x)=\left| x \right|wird zu
Vektoren, Matrizen und Determinanten
Für Vektoren und Matrizen wird innerhalb der -Umgebung eine weitere Umgebung benötigt:
Vektoren und Matrizen
Umgebung | Verwendung |
|---|---|
pmatrix | Mit der "pmatrix"-Umgebung kannst du Vektoren und Matrizen erstellen. Zeilen werden mit |
Mit dem Code
\vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}erhältst du den Vektor
Wenn du zwei Punkte mit einem Vektorpfeil darstellen willst, geht das mit
\overrightarrow{PQ}Dann erhältst du
Durch die Eingabe
A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}wird die folgende Matrix erzeugt:
Determinanten
Für die Darstellung von Determinanten wird die folgende Umgebung verwendet:
Umgebung | Verwendung |
|---|---|
vmatrix | Die "vmatrix"-Umgebung ist nützlich für die Notation von Determinanten. Einzelne Spalten werden mit |
So wird beispielsweise durch die Eingabe
\det A = \begin{vmatrix} 2 & 2 & 5 \\ 1 & 3 & 9 \\ 2 & 3 & 4 \end{vmatrix}die folgende Determinate erzeugt:
Integrale
Um Integrale darzustellen, wird der Befehl \int verwendet. Soll es sich nicht um ein unbestimmtes, sondern um ein bestimmtes Integral handeln, so können die untere und obere Grenze durch die Ergänzung \int_{ }^{ } ergänzt werden. Dabei bestimmt der Inhalt des Klammerpaares nach _ die untere Grenze, während der Inhalt des Klammerpaares nach ^ den Inhalt der oberen Grenze festlegt.
Ausgabe | LaTeX-Code | Erklärung |
|---|---|---|
\int_{-\pi}^{\pi} \sin(x) \mathrm{d}x | Integralgrenzen mit _ und ^, sowie den Operator "d" in normaler Schriftart mit \mathrm{} |
Bei der Darstellung der Integrationsvariablen ist zu beachten, dass man nicht dx, sondern stattdessen \mathrm{d}x schreibt.
Pfeile
In diesem Abschnitt geht es um die Darstellung von Pfeilen.
Liste mathematischer Ausdrücke
Funktionen
Mathematische Sonderzeichen
Eine Auflistung der wichtigsten mathematischen Sonderzeichen findest du hier:
Schreibweisen und Funktionsmodifikationen
Sonderzeichen, Vektorpfeile, Ableitungen oder geschweifte Klammern unter Termen findest du hier:
