1 Übersicht
Inhalt des Kurses
Du lernst in diesem Kurs …
was eine gestreckte, gestauchte und gespiegelte Parabel ist.
was der Öffnungsfaktor einer Parabel ist.
wie man den Öffnungsfaktor einer vorgegebenen Parabel bestimmen kann.
Vorkenntnisse
Bevor du diesen Kurs beginnst, solltest du wissen, …
was eine Normalparabel ist.
was ein Funktionsgraph ist und wie man diesen in ein Koordinatensystem einzeichnet.
wie man lineare Gleichungen löst.
Kursdauer
Der Kurs dauert ca. 45 Minuten.
2 Motivation

Die Rakotzbrücke im Kromlauer Park hat die Form einer quadratischen Funktion, jedoch nicht die einer Normalparabel. Wie könnte der Funktionsterm lauten?

Marco wirft in der letzten Minute auf den freien Korb. Zum Glück versteht er etwas von Mathematik und wirft die perfekte Parabel!
Welche Form wird diese Parabel beschreiben? Wie könnte ein Funktionsterm lauten?
3 Wie kann man Breite und Öffnung einer Parabel verändern?
Mit einer Normalparabel der Form kannst du manche Sachverhalte wie beispielsweise die Brücke oder die Flugbahn des Basketballes nicht mit einem Funktionsgraph abbilden.
Du kannst allerdings Parabeln strecken oder stauchen, also "enger" oder "breiter" als die Normalparabel machen.
Zudem kannst du Parabeln an der -Achse spiegeln, sodass sie nach unten geöffnet ist.
Gestreckte Parabel | Normalparabel | Gestauchte Parabel |
|---|---|---|
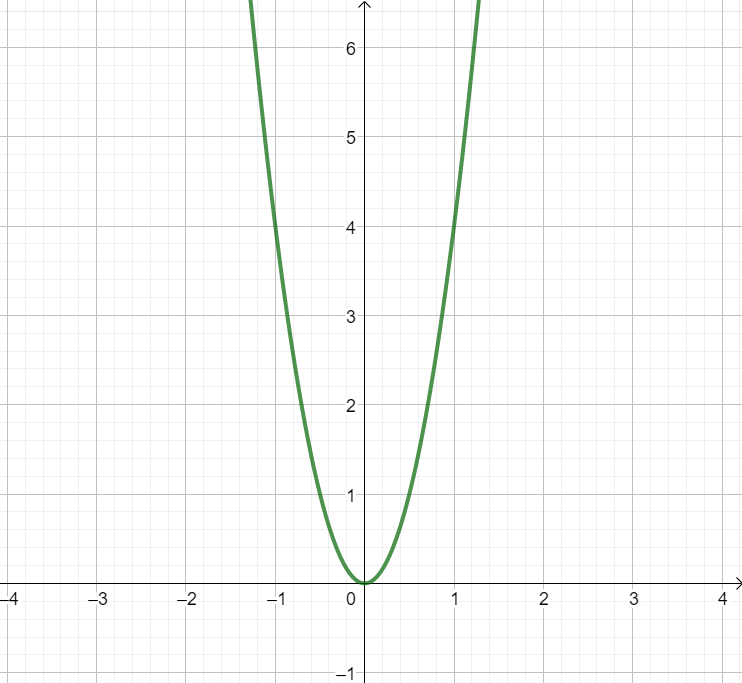 | 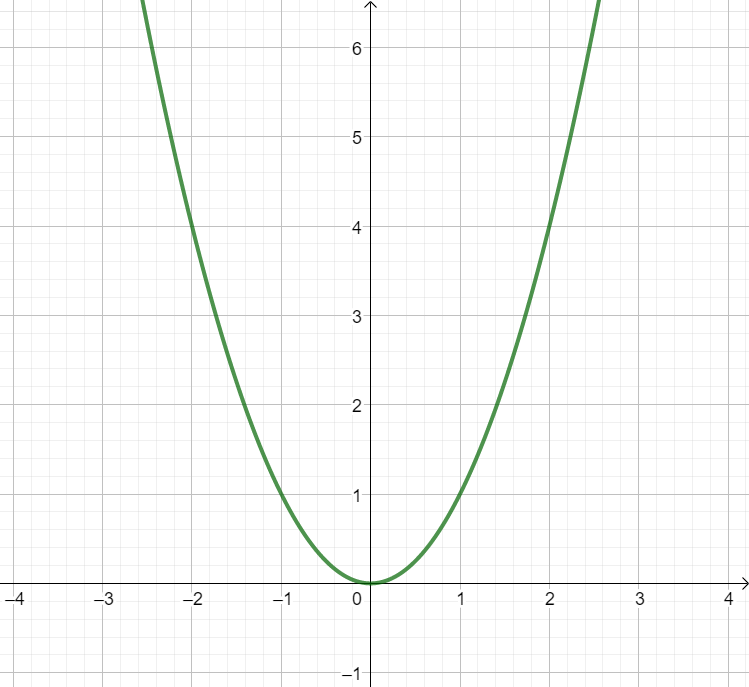 | 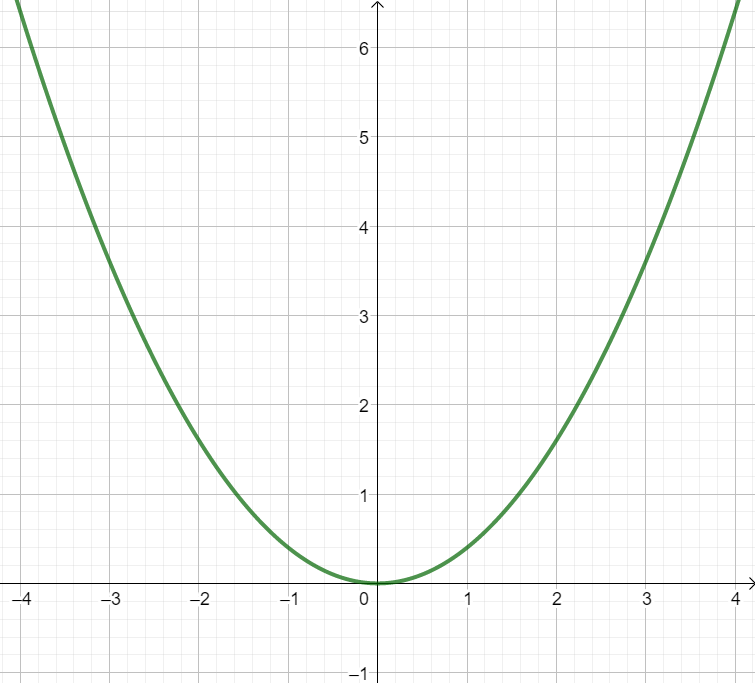 |
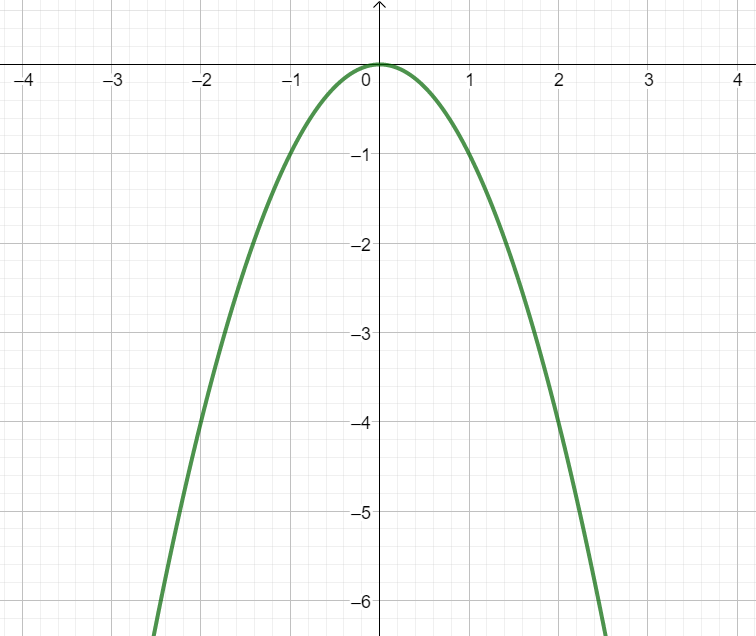
gespiegelte Normalparabel
Die Parabel hat dann die Funktion . Es steht also ein Faktor vor dem , das den Funktionsgraphen staucht oder streckt. Diesen Faktor nennt man Öffnungsfaktor.
4 Wirkung des Öffnungsfaktors (1/3)
Bearbeite die folgende Aufgabe und beobachte, wie sich der Öffnungsfaktor auf den Funktionsgraphen der Parabel auswirkt.
Laden
5 Wirkung des Öffnungsfaktors (2/3)
Der Öffnungsfaktor kann auch negativ werden. Bearbeite die folgende Aufgabe anhand des Applets und beobachte die Wirkung von auf den Funktionsgraphen, wenn er negative Werte annimmt!
Laden
6 Wirkung des Öffnungsfaktors (3/3)
Hier findest du nochmal eine Zusammenfassung der Ergebnisse aus den vorangegangenen Aufgaben.
Öffnungsfaktor | Funktionsgraph | Beschreibung des Funktionsgraphen |
|---|---|---|
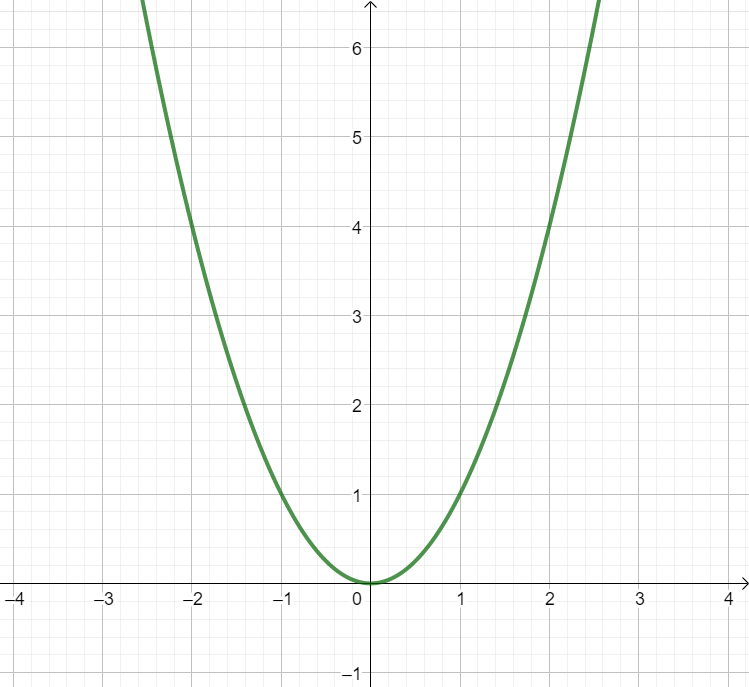 | Normalparabel | |
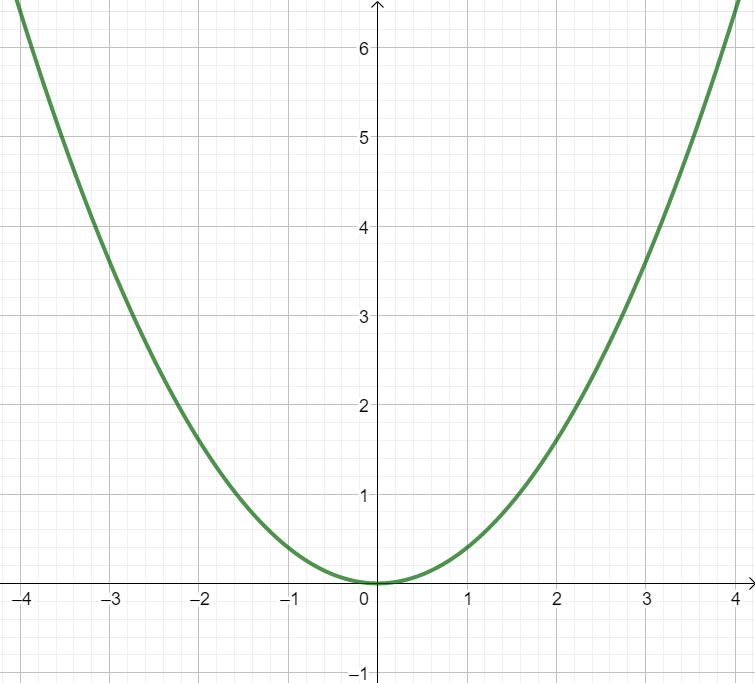 z.B. |
| |
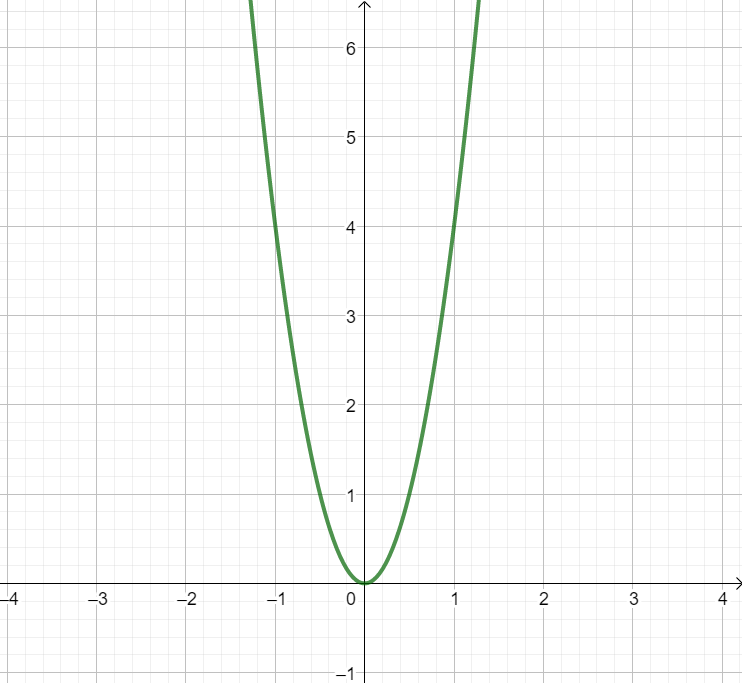 z.B. |
| |
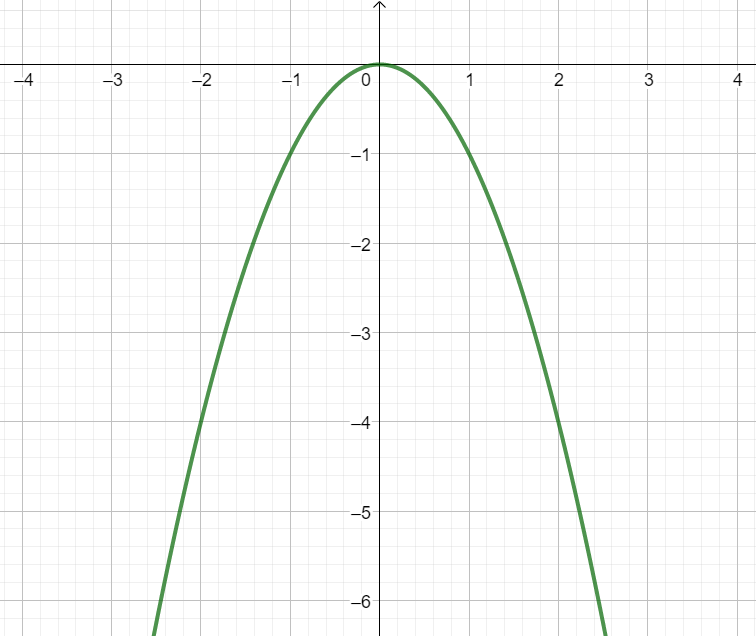 |
| |
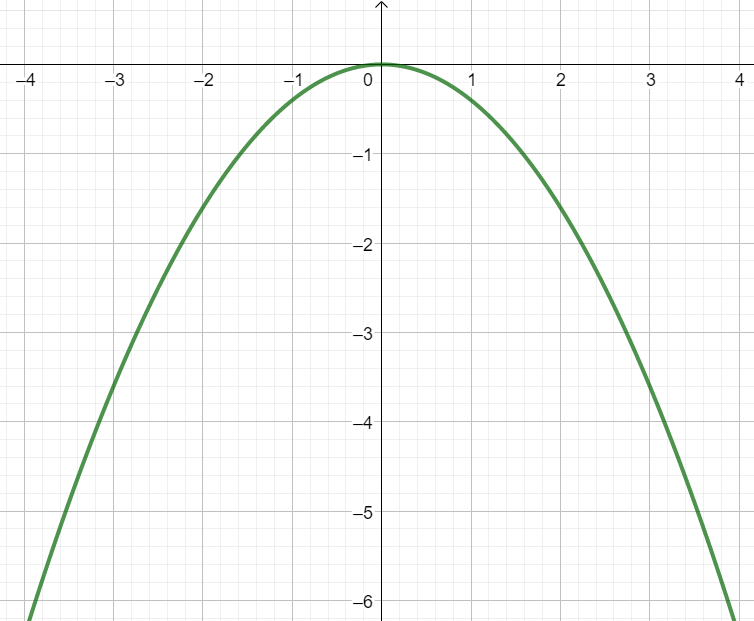 z.B. |
| |
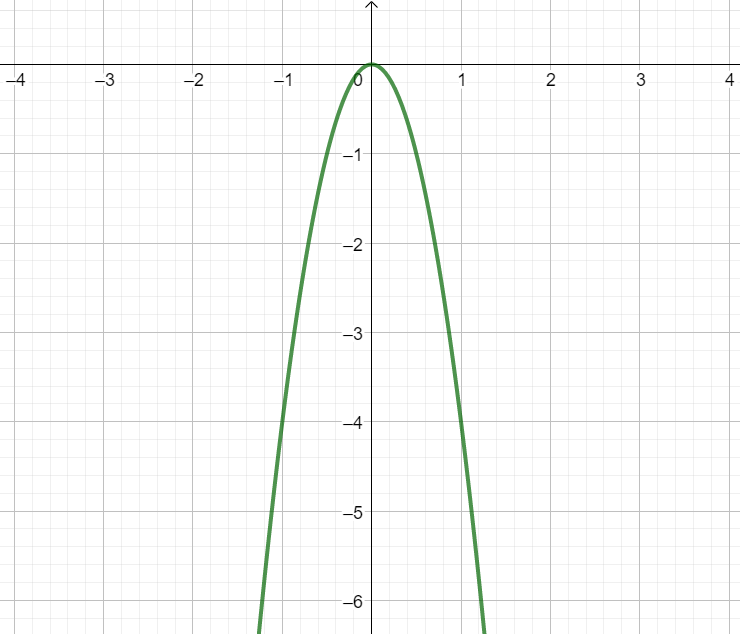 z.B. |
|
7 Öffnungsfaktor bestimmen
Du weißt jetzt, wie sich Öffnungsfaktoren auf den Funktionsgraphen einer Parabel auswirken.
Aber wie kannst du den richtigen Öffnungfaktor bestimmen, wenn du einen Funktionsgraphen einer Parabel hast?
Beispiel Schau dir diese Parabel an:
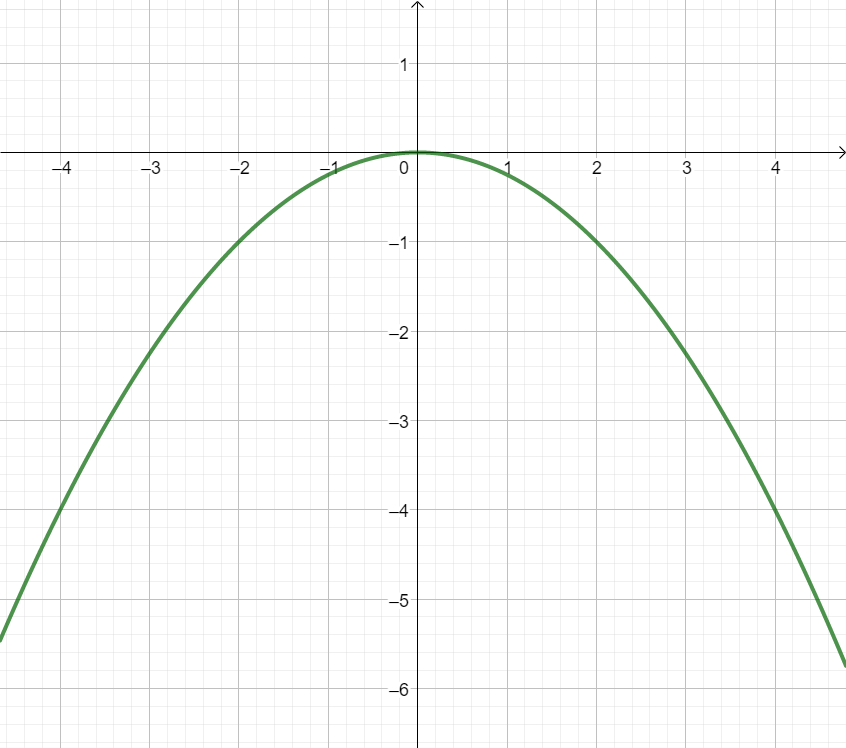
Du kannst sofort erkennen, dass diese Parabel nach unten geöffnet ist und gestaucht. Du weißt also, dass der Öffnungsfaktor negativ sein muss.
Bei einer Parabel mit dem Scheitelpunkt kann man den Öffnungsfaktor im Punkt ablesen. Im Beispiel kann man diesen Punkt leider nicht genau ablesen, aber man kann schon erkennen, dass a zwischen und liegt.
Um den Öffnungsfaktor herauszufinden benötigst du einen Punkt, der nicht der Scheitelpunkt ist. Gut ablesen kann man den Punkt .
Die Koordinaten des Punktes setzt du in die Funktionsgleichung ein.
Du erhältst also eine lineare Gleichung, die du nach auflösen kannst.
Du erhältst also für den Öffnungsfaktor .
Als Funktionsgleichung erhältst du .
8 Aufstellen der Funktionsgleichung
Laden
9 Die Flugbahn des Basketballs
Du erinnerst dich sicher an Marco, der den Basketball mit einer perfekten Parabeln in den Korb wirft.
Wir können nun die Funktionsgleichung der Flugbahn bestimmen.

Wir integrieren dazu das Bild in ein Koordinatensystem…
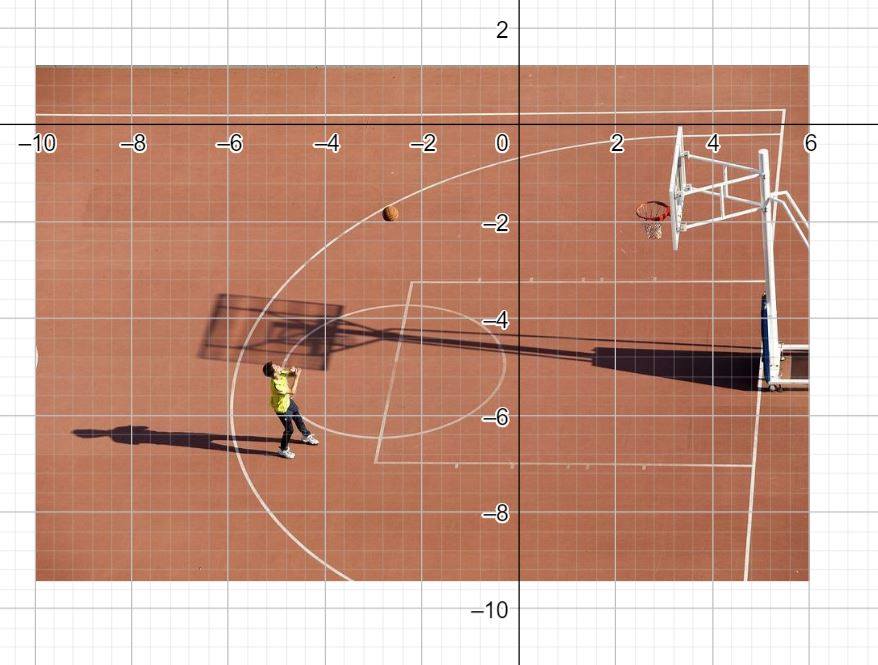
…und lesen die Koordinaten des Basketballes ab.
Der Ball hat also die Koordinaten .
Nehmen wir nun an, dass sich der Scheitelpunkt der Parabel wieder im Ursprung befindet.
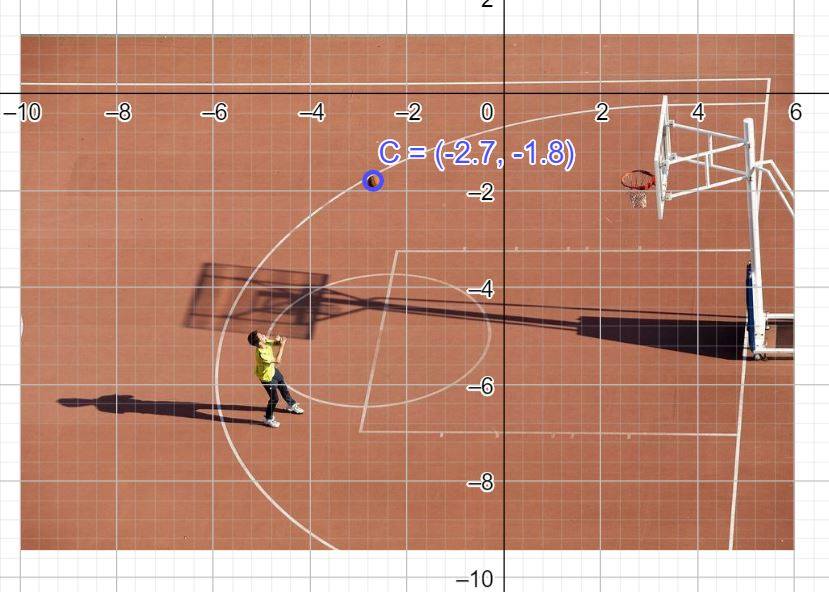
Berechne nun den Funktionsterm der Parabel und überprüfe anschließend mit dem Applet.
