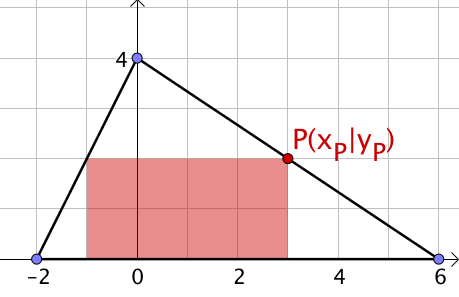
Dem abgebildeten Dreieck soll ein Rechteck mit möglichst großem Flächeninhalt einbeschrieben werden.
Berechne den größtmöglichen Flächeninhalt.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe
Bei dieser Aufgabe ist einem Dreieck ein größtmögliches Rechteck einzubeschreiben. Es handelt sich also um eine Extremwertaufgabe
Wenn du eine Rechtecksseite auf die Grundlinie des Dreiecks legst, bedeutet die Forderung des "Einbeschreibens", dass die beiden weiteren Rechteckspunkte und jeweils auf den anderen Seiten des Dreiecks liegen. Dies ergibt zwei Nebenbedingungen für die Extremwertaufgabe.
Da der Flächeninhalt maximiert werden soll, benötigst du zunächst als Zielfunktion die Formel für den Flächeninhalt eines Rechtecks, in die du dann die Nebenbedingungen "einarbeiten" musst.
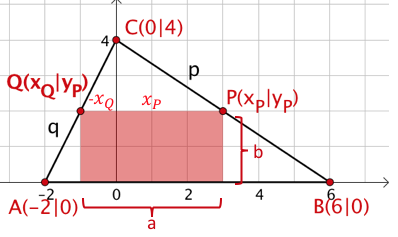
Zielfunktion
mit und also:
1. Nebenbedingung
liegt auf der Geraden .
Stelle die Gleichung der Geraden mit Hilfe der Punkte und auf.
Gib nun die 2. Nebenbedingung an.
2. Nebenbedingung
liegt auf der Geraden .
Stelle die Gleichung der Geraden mit Hilfe der Punkte und auf.
Löse nach auf.
| ↓ | Setze für den Term aus (1) ein. | ||
| ↓ | Multipliziere die Klammer aus | ||
Setze und in die Zielfunktion ein, um die Zielfunktion in Abhängigkeit der einzigen Variablen zu erhalten.
| ↓ | Multipliziere aus | ||
Bilde die Ableitung .
Setze gleich Null und löse die Gleichung.
Überprüfe mit der 2. Ableitung, ob sich für tatsächlich ein Maximum ergibt.
ist eine konstante Funktion. Somit ist auch und ergibt eine größtmögliche Rechtecksfläche.
Setze in die Fläche ein.
Flächeninhalt:
Setze auch noch in die 1. Nebenbedingung ein, um die 2. Koordinate des Eckpunktes P zu erhalten.
Nebenbedingung:
Ergebnis:
Mit dem Eckpunkt ist das größtmögliche Rechteck in das Dreieck einbeschrieben und hat den Flächeninhalt .
Alternative Lösung 1
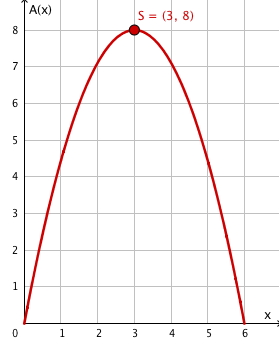
Der Graph der Zielfunktion
ist eine nach unten geöffnete Parabel.
Ihr Maximum ist der Scheitelpunkt. Diesen kann man - außer über die Ableitung von - durch eine quadratische Ergänzung ermitteln.
| ↓ | Klammere aus. | ||
| ↓ | |||
| ↓ | 2. binomische Formel benutzen. | ||
Lies den Scheitelpunkt ab
Dessen 2. Koordinate liefert den gesuchten maximalen Flächeninhalt eines dem Dreieck einbeschriebenen Rechtecks.
Im nachfolgenden Applet kannst du durch Verschieben des Punktes P das Ergebnis kontrollieren.
Alternative Lösung 2
Die gestellte Aufgabe lässt eine verblüffend einfache Lösung zu. Dabei wird das Koordinatensystem nicht benötigt, sondern sie ergibt sich aus dem Strahlensatz.
Entscheidend für diese Möglichkeit ist, dass vom Dreieck neben der Grundlinie die Höhe auf diese Seite mit gegeben ist.
Zielfunktion ist die Formel für die Fläche des Rechtecks mit den Seitenlängen und . Also:
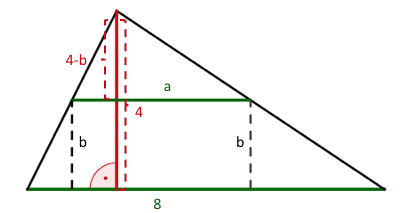
Die Nebenbedingung ergibt sich aus dem Strahlensatz.
Benutze den Strahlensatz und erhalte:
Setze in ein.
Die Zielfunktion ist eine nach unten geöffnete Parabel. Deshalb ergibt die y-Koordinate des Scheitelpunktes den maximal möglichen Flächeninhalt einbeschriebener Rechtecke.
Den Scheitelpunkt berechnest du über die Ableitung von oder mit einer quadratischen Ergänzung.
Ableitung von
quadratische Ergänzung
Vertiefung der Aufgabe
In der gegebenen Aufgabenstellung soll das Rechteck dem Dreieck so einbeschrieben werden, dass eine Rechteckseite auf der Grundseite liegt.
Natürlich kann man Rechtecke auch so einbeschreiben, dass eine Rechteckseite auf einer der beiden anderen Dreieckseiten liegt.
Dann stellt sich die Frage: Haben die maximal möglichen Flächeninhalte auch bei den beiden anderen Lagen den gleichen Wert?
Dass dies tatächlich so ist, kannst du am folgenden Applet nachvollziehen, indem du die unterschiedlichen Gleitpunkte , oder verschiebst.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?
