Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgabe lösen
Abstand eines Punktes von einer Geraden Bei dieser Aufgabe bestimmst du als Extremwertaufgabe denjenigen Punkt der Geraden, der von einem gegebenen Punkt außerhalb der Geraden den kleinsten Abstand hat.
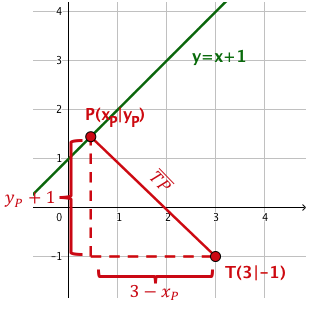
Der Zeichnung entnimmst du die Zielfunktion und die Nebenbedingung dieser Extremwertaufgabe.
Zielfunktion
Abstand der Punkte P T
Nebenbedingung
Der Punkt P
y = x + 1
T P 2 ( x P ; y P ) = ( 3 − x P ) 2 + ( y P + 1 ) 2 ↓ Setze die Geradengleichung für y ein.
T P 2 ( x p ) = ( 3 − x p ) 2 + ( x p + 2 ) 2 ↓ Quadriere aus
T P 2 ( x p ) = 9 − 6 x p + x p 2 + x p 2 + 4 x p + 4 ↓ Fasse zusammen
T P 2 ( x p ) = 2 ( x p ) 2 − 2 x p + 13 ↓ Ziehe die Wurzel
T P ( x P ) = 2 ( x P ) 2 − 2 x P + 13
Beachte für Extremwertaufgaben mit einer Abstandsbedingung:
Für alle Punkte, für die der Abstand minimal oder maximal wird, ist auch das Quadrat des Abstandes minimal bzw. maximal, da gilt:
0 < T P 1 < T P 2 ⇔ T P 1 2 < T P 2 2
Da die Ableitung für T P 2 T P Quadrat des Abstandes.
T P 2 ( x P ) = 2 ( x P ) 2 − 2 x P + 13 ↓ Bilde die Ableitung
T P 2 ( x P ) ′ = 4 x P − 2 ↓ Setze die Ableitung gleich Null
0 = 4 x P − 2 + 2 2 = 4 x P : 4 0,5 = x p
Berechne die 2. Ableitung der Zielfunktion, um dich zu versichern, dass x P = 0,5 Minimum des Quadrats des Abstandes liefert.
T P 2 ( x P ) ′ ′ = + 4 > 0
⇒ x P = 0,5
liefert Minimum .
Bestimme jetzt aus der Nebenbedingung y P
y P = 0,5 + 1 = 1,5
⇒ P ( 0,5 | 1,5 )
Berechne abschließend T P T P 2
Ergebnis:
Der minimale Abstand des Punktes T ( 3 | − 1 ) y = x + 1
T P LE = 2 ⋅ 0,25 − 2 ⋅ 0,5 + 13 LE = 12,5 LE ≈ 3,54 LE .
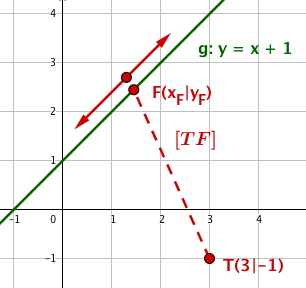
Alternative Lösung Ohne Kenntnisse aus der Differenzialrechnung kannst du die Aufgabe auch mit einer geometrischen Überlegung lösen:
Der gesuchte Punkt der Geraden g T Lotfußpunkt F T g
Er kann
a) als Gleitpunkt auf der Geraden oder
b) als Schnittpunkt zweier Geraden
berechnet werden.
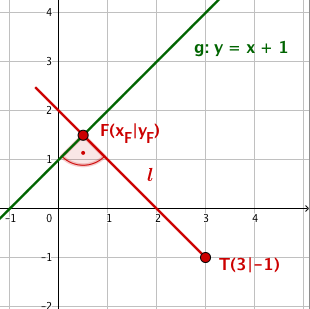
a) Der Lotfußpunkt F g
Wenn die Strecke [ A F ] g m [ T F ] m g gelten :
m [ T F ] ⋅ m g = − 1
Also:
y F + 1 x F − 3 ⏟ = m [ T F ] ⋅ 1 ⏟ = m g = − 1 ↓ Setze die Geradengleichung für y ein
x F + 2 x F − 3 = − 1 ⋅ ( x F − 3 ) x F + 2 = − x F + 3 + x F − 2 2 x F = 1 : 2 x F = 0,5
b) Der Lotfußpunkt F g g
Im nachfolgenden Applet kannst du die Rechnung überprüfen, indem du den Geradenpunkt F
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von
GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer
Datenschutzerklärung .
[https://www.geogebra.org/material/iframe/id/pKD3xcuA]