1 Übersicht
Inhalt des Kurses
Dieser Kurs ist eine Einführung in die Menge der "Rationalen Zahlen".
Vorwissen
Du solltest wissen, was die Menge der ganzen Zahlen ist. Außerdem sind Kenntnisse rund um das Thema der Brüche und Dezimalbrüche notwendig.

Dauer
Die Bearbeitung des Kurses dauert ca. 50 min.
2 Erweiterung von ganzen Zahlen (1/3)

3 Erweiterung von ganzen Zahlen (2/3)

Du kennst bereits die natürlichen Zahlen
und die ganzen Zahlen .
Ebenso hast du schon Brüche wie z.B. oder kennengelernt. Diese lassen sich jedoch weder den natürlichen Zahlen , noch den ganzen Zahlen zuordnen.
4 Erweiterung von ganzen Zahlen (3/3)
Brüche gehören zu den rationalen Zahlen .
Rationale Zahlen kann man auch als Dezimalbruch darstellen.
Zum Beispiel gilt:
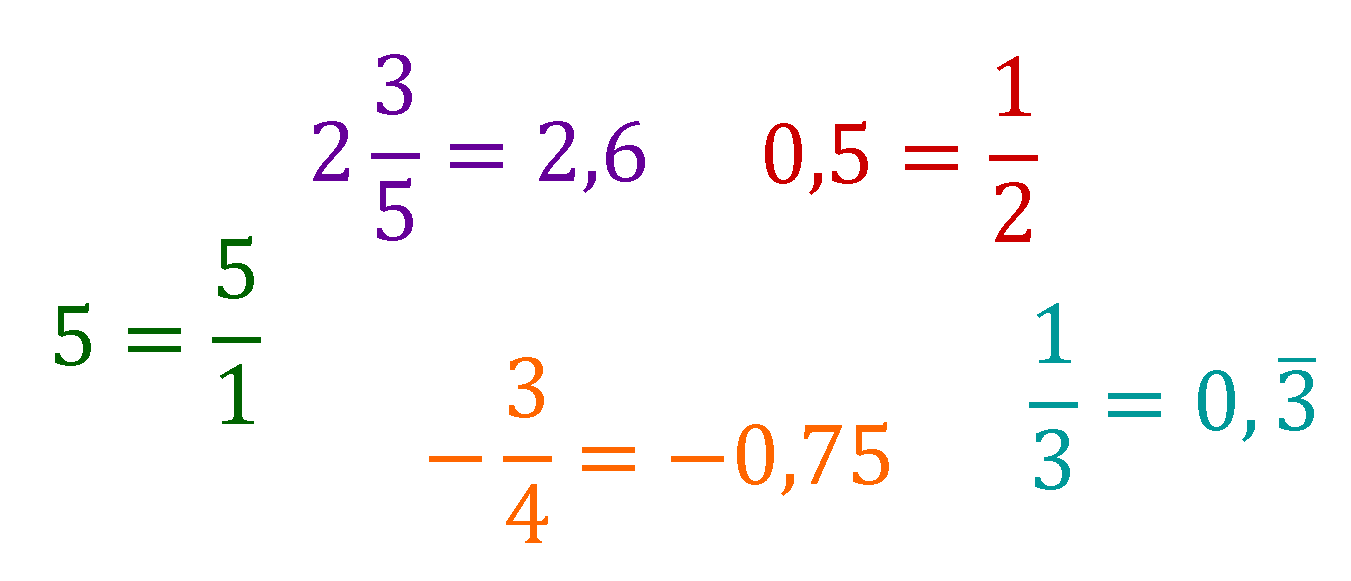
Dezimalbrüche von rationalen Zahlen haben nur endlich viele Nachkommastellen oder sind periodisch.
Die Menge der rationalen Zahlen enthält also alle Zahlen, die sich als
endliche Dezimalzahlen
periodische Dezimalzahlen
5 Definition: rationale Zahlen
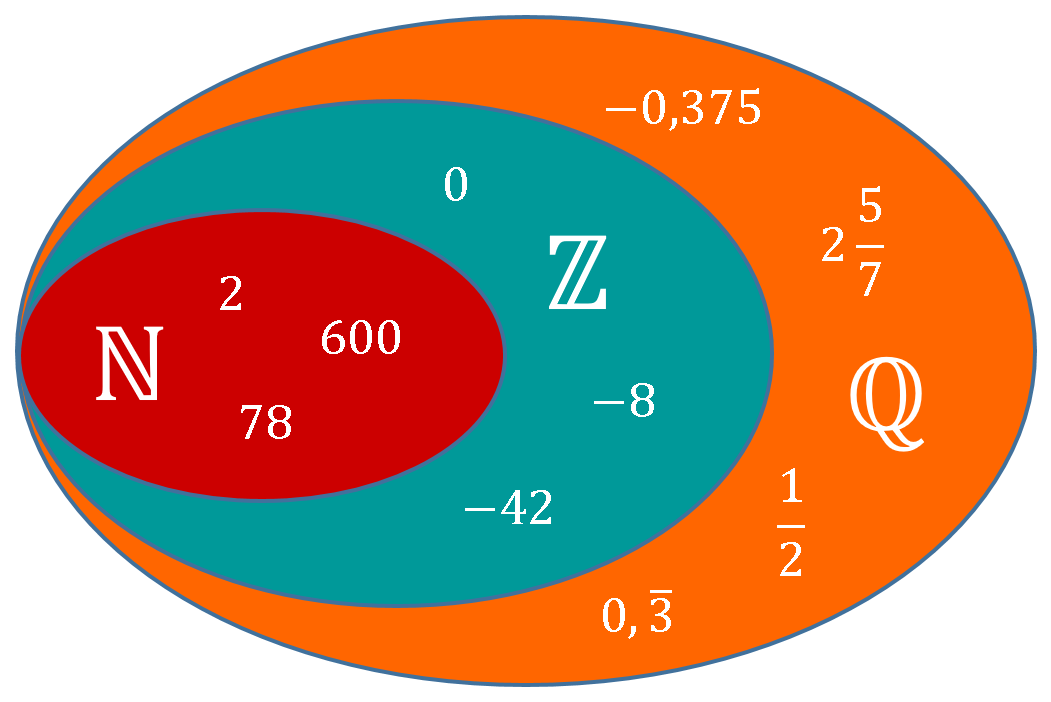
Jede rationale Zahl lässt sich als vollständig gekürzter Bruch in der Form darstellen, wobei der Zähler eine ganze Zahl und der Nenner eine natürliche Zahl ist.
Symbolisch bezeichnet man die rationalen Zahlen mit .
Zum Beispiel sind folgende Zahlen in der Menge der rationalen Zahlen enthalten:
.
6 Zahlen sind nicht eindeutig in der Darstellung
Mathematicus ist verwirrt und wendet sich an seinen Professor, den Hut:

Du kannst also jede beliebige Zahl auf viele verschiedene Arten ausdrücken. Dazu kannst du sie als Bruch schreiben oder als Dezimalzahl.
Beispiele
7 Aufgaben zu unterschiedlichen Darstellungen der Zahlen
Laden
Laden
8 Die Zahlengerade in den rationalen Zahlen
Zahlenstrahl in den natürlichen Zahlen
Betrachte nebenstehendes Bild. Die Zahlengerade der natürlichen Zahlen beginnt bei 1 und läuft dann in Einerschritten immer weiter ins Unendliche.

Zahlenstrahl (Zahlenhalbgerade) in den natürlichen Zahlen
Zahlenstrahl in den ganzen Zahlen
Bei den ganzen Zahlen geht man auch in Einerschritten die Zahlenstrahl ab. Allerdings kann man hier auch Schritte in Richtung der negativen Zahlen gehen.
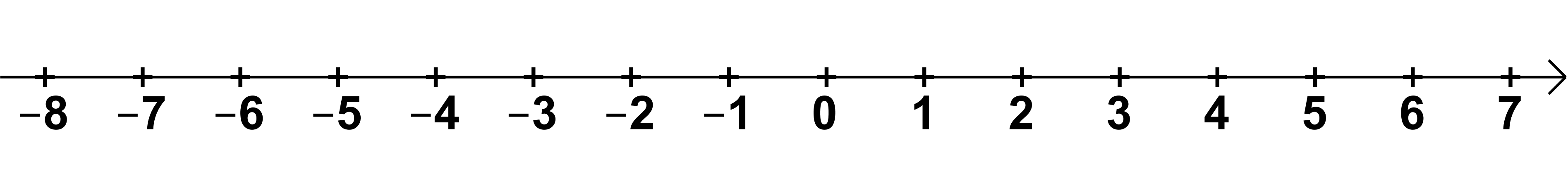
Zahlenstrahl in den ganzen Zahlen
Zahlengerade in den rationalen Zahlen
Auf der Zahlengeraden kannst du jetzt beliebig kleine Schritte gehen und kannst dadurch auch bei Zahlen wie z. B. oder landen.
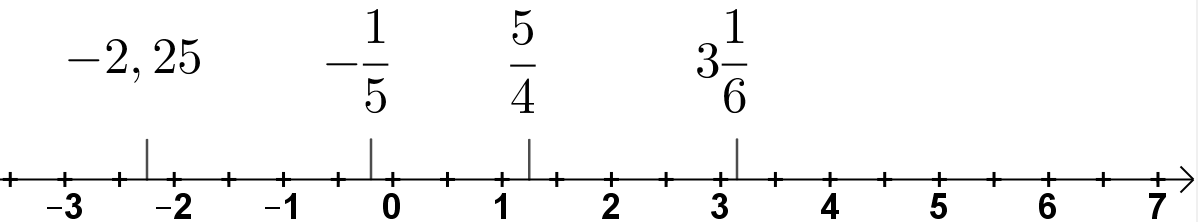
Zahlengerade in den rationalen Zahlen
9 Aufgaben zur Zahlengerade in den rationalen Zahlen
Laden
Laden
10 Dichtheit
Wie du auf den vorherigen Kursseiten sehen konntest, kannst du von einem Startpunkt aus in beliebig kleinen bzw. großen Schritten die Zahlengerade auf und ablaufen.

Beispiel: | In den ganzen Zahlen | In den rationalen Zahlen |
|---|---|---|
Zwischen und | ||
Zwischen und | keine | |
Zwischen und | keine |
11 Zusammenfassung
Du hast in diesem Kurs folgendes kennengelernt:
Brüche gehören zu den rationalen Zahlen .
Rationale Zahlen kann man auch als Dezimalbrüche darstellen.
Du kannst jede beliebige Zahl auf viele verschiedene Arten ausdrücken.
Auf der Zahlengeraden in den rationalen Zahlen kannst du beliebig kleine Schritte gehen.
Die Menge der rationalen Zahlen ist dicht.

