Funktionsterme bestimmen

Zum "roten Graphen" gehört eine Funktion dritten Grades $f(x)$ mit dem Hochpunkt $\mathrm{HP}\left(0|1\right)$ (hier ist $f'(x)=0$) und dem Tiefpunkt $\mathrm{TP}\left(2|-3\right)$ (hier ist $f'(x)=0$). Trage diese Informationen in eine Tabelle ein.

Die allgemeine Funktion $3.$ Grades lautet:

$f(x)=ax^3+bx^2+cx+d$ und die erste Ableitung ist dann:

$f'(x)=3ax^2+2bx+c$

Nach der Tabelle ergibt die Gleichung $\mathrm{(I)}$:

$1=a\cdot 0+b\cdot 0+c \cdot 0+d\;\Rightarrow\;d=1$

Gleichung $\mathrm{(II)}$ ergibt: $0=3a\cdot 0+2b\cdot 0+c\;\Rightarrow\;c=0$

Gleichung $\mathrm{(III)}$ ergibt unter Berücksichtigung der bisherigen Ergebnisse:

$-3=a\cdot 2^3+b\cdot 2^2+0\cdot 2+1$$\;\Rightarrow\;-3=8a+4b+1\;\Rightarrow\;-4=8a+4b$$\;\Rightarrow\;-1=2a+b\;\Rightarrow\;b=-1-2a$

Gleichung $\mathrm{(IV)}$ ergibt unter Berücksichtigung der bisherigen Ergebnisse:

$0=3a\cdot 2^2+2b\cdot2+0\;\Rightarrow\;0=12a+4b\;\Rightarrow\;0=3a+b$

Das Ergebnis aus Gleichung $\mathrm{(III)}$ $b=-1-2a$ in $\mathrm{(IV)}$ $0=3a+b$ eingesetzt ergibt:

$0=3a+(-1-2a)=3a-1-2a=a-1\;\Rightarrow\;a=1$

Mit $a=1$ folgt in $\mathrm{(III)}:$ $b=-1-2\cdot1=-3$

Antwort: Die Funktion $3.$ Grades lautet: $f(x)=x^3-3x^2+1$

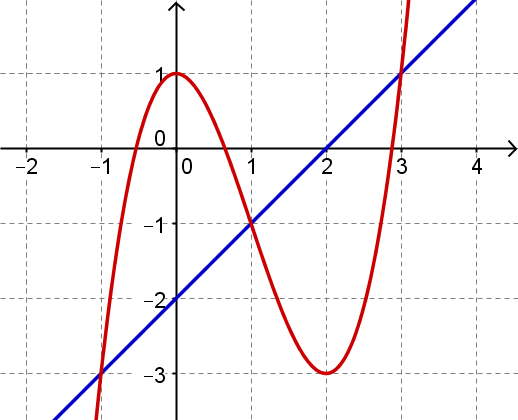
Zum "blauen Graphen" gehört eine lineare Funktion $g(x)$. Aus der Abbildung kannst du die Steigung $m=1$ und den $y$-Achsenabschnitt $t=-2$ ablesen: $\;\Rightarrow\;g(x)=x-2$

Antwort: Die Gleichung der linearen Funktion lautet: $g(x)=x-2$

Bestimmung der Schnittpunkte der beiden Graphen

"Die beiden abgebildeten Graphen schneiden sich in drei Punkten, die jeweils ganzzahlige Koordinaten besitzen". Deshalb können die Schnittpunkte aus der Abbildung abgelesen werden.

Antwort: Die Schnittpunkte haben folgende Koordinaten: $S_1(-1|-3); S_2(1|-1); S_3(3|1)$

Wie kannst du den gesamten Inhalt $A$ der von den beiden Graphen eingeschlossenen Fläche mit bestimmten Integralen angeben?

Flächeninhalt:

$A=A_1+A_2=\int_{-1}^{1}\left(f(x)-g(x)\right) \mathrm{d}x+\int_{1}^{3}\left(g(x)-f(x)\right) \mathrm{d}x$

Berechnung von $A$:

$f(x)-g(x)=x^3-3x^2+1-(x-2)=x^3-3x^2-x+3$

$g(x)-f(x)=-(f(x)-g(x))=-(x^3-3x^2-x+3)=-x^3+3x^2+x-3$

$A_1=\int_{-1}^{1}\left(x^3-3x^2-x+3\right) \mathrm{d}x=\left[\frac{1}{4}\cdot x^4-x^3-\frac{1}{2}\cdot x^2+3x\right]_{-1}^{1}$

$=\left(\frac{1}{4}-1-\frac{1}{2}+3\right)-\left(\frac{1}{4}-(-1)-\frac{1}{2}+3\cdot(-1)\right)=1{,}75-(-2{,}25)=4$

$A_2=\int_{1}^{3}\left(-x^3+3x^2+x-3\right) \mathrm{d}x=\left[-\frac{1}{4}\cdot x^4+x^3+\frac{1}{2}\cdot x^2-3x\right]_{1}^{3}$

$=\left(-\frac{1}{4}\cdot3^4+3^3+\frac{1}{2}\cdot3^2-3\cdot 3\right)-\left(-\frac{1}{4}+1+\frac{1}{2}-3\right)=2{,}25-(-1{,}75)=4$

$A_{gesamt}=A_1+A_2=4+4=8$

Antwort: Der von den beiden Graphen eingeschlossene Flächeninhalt beträgt $8\;\mathrm{FE}$.