Aus einer rechteckigen Fensterscheibe mit den Seitenlängen und , ist vom unteren Mittelpunkt der kleineren Seite aus, eine Ecke geradlinig unter einem Winkel von 45° abgesprungen.
Aus der restlichen Scheibe soll durch Schnitte parallel zu den ursprünglichen Seiten eine möglichst große rechteckige Scheibe hergestellt werden.
Welche Seitenlängen und welche Fläche hat die "Ersatzscheibe"? In welchem Punkt setzen die Schnitte an?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Extremwertaufgaben
Bei dieser Aufgabe soll ein größtmöglicher Flächeninhalt bestimmt werden. Es handelt sich also um eine Extremwertaufgabe.
Die Scheibe sei höher als breit. Also gelte: .
Das abgeschnittene Stück der Scheibe ist wegen des Neigungswinkels von 45° ein gleichschenklig-rechtwinkliges Dreieck mit der Kathetenlänge von .
Die gesuchte rechteckige "Ersatzscheibe" habe die Seitenlängen und und entsteht von einem Punkt aus, der auf der abgebrochenen Schnittkante variiert.
Die Zielfunktion ist der Flächeninhalt eines Rechtecks mit den Seiten und :
,
wobei
und
Grafische Veranschaulichung
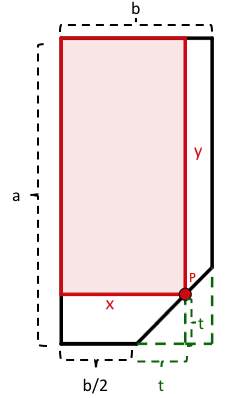
Die Nebenbedingungen für ergeben sich aus dessen variabler Lage auf der Schnittkante und können mit einem variablen Parameter so angegeben werden:
Setze die Nebenbedingungen in die Zielfunktion ein, um diese als Funktion der Variablen zu erhalten.
Zielfunktion
| ↓ | Bilde - z.B. mit der Produktregel - die 1. Ableitung und die 2. Ableitung . | ||
| ↓ | Setze gleich Null und löse die Gleichung. | ||
Zwischenstand der Lösung:
Die gesuchte Ersatzscheibe mit maximalem Flächeninhalt wird von einem variablen Punkt P aus erzeugt, der auf der Strecke liegen muss.
Damit ist der Definitionsbereich der Flächen-Zielfunktion auf das Intervall begrenzt.
ist wegen eine nach unten geöffnete Parabel und der errechnete Wert liefert ein lokales Maximum - also einen maximalen Flächeninhalt, aber nur dann, wenn der Wert im Intervall liegt.
Da ist jedenfalls .
ist aber nicht für jedes Zahlenpaar und kleiner als , da gilt:
Fallunterscheidung:
Fall 1: ("a nicht zu groß")
Fall 2:("a beliebig groß")
Setze in ein.
Fall 1:
liefert lokales Maximum
Die Seitenlängen der Ersatzscheibe sind:
Die Ersatzscheibe ist demnach ein Quadrat.
Für den Punkt auf , von dem aus geschnitten wird gilt:
Zahlenbeispiel
Am nachfolgenden Applet kannst du die Aufgabe mit den Zahlenwerten und nachvollziehen. Verschiebe dazu den Erzeugungspunkt längst der Bruchkante .
Man erhält für den maximalen Flächeninhalt , für die (quadratische) Rechtecksseite und für den Abstand des Punktes von den Wert
Fall 2
Damit liegt der Scheitelpunkt der Flächenparabel rechts vom Intervall und nimmt in diesem Intervall streng monoton zu.
Die größte Fläche wird demnach - als Randextremum - angenommen, wenn der erzeugende Punkt mit dem rechtem Randpunkt zusammenfällt. Also für .
Demnach gilt hier:
.
Die Seitenlängen für sind:
und .
Für den erzeugenden Punkt gilt: .
Zahlenbeispiel
Am nachfolgenden Applet kannst du die Aufgabe mit den Zahlenwerten und nachvollziehen. Verschiebe dazu den Erzeugungspunkt längs der Bruchkante .
Man erhält für den maximalen Flächeninhalt , bei den Seitenlängen von und .
Zusammenfassung
Die Aufgabe ist durch die notwendige Fallunterscheidung der Fenstermaße anspruchsvoll.
Falls die Fensterhöhe "nicht zu groß" gegenüber der Fensterbreite ist (), besitzt die Aufgabe ein lokales Maximum.
Falls die Fensterhöhe "zu groß" gegenüber der Fensterbreite ist () ergibt sich ein Randmaximum.
Alternative Lösung
Die beschriebene Lösung hat für die variable Lage des Erzeugungspunktes auf der Bruchkante seinen horizontalen Abstand vom Punkt als Parameter verwendet.
Für eine alternative Lösung der Aufgabe verzichten wir auf einen zusätzlichen Parameter und betrachten die Rechtecksseiten und als die Variablen des gesuchten maximalen Rechtecks und bestimmen die Nebenbedingung zwischen und aus dem Strahlensatz.
Die Zielfunktion lautet:
mit
Die Nebenbedingung ergibt sich durch Anwendung des Strahlensatzes in der nebenstehenden Skizze:
Grafische Veranschaulichung
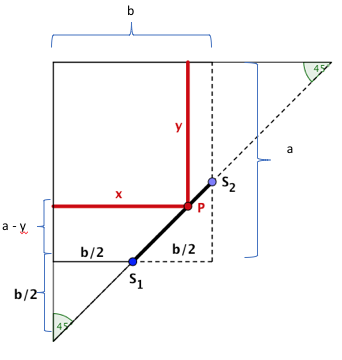
Setze das Ergebnis der Nebenbedingung in die Zielfunktion ein.
| ↓ | Setze gleich Null, um ein mögliches Maximum zu erhalten. | ||
| ↓ | mit | ||
Zwischenstand der alternativen Lösung
Die gesuchte Ersatzscheibe mit maximalem Flächeninhalt ist ein Rechteck mit den Seitenlängen und .
Dabei muss eine Zahl aus dem Intervall sein, damit der erzeugende Punkt auf der Strecke liegt.
Durch die Nebenbedingung aus dem Strahlensatz ergibt sich mit eine nach unten geöffnete Parabel und liefert ein lokales Maximum für die Rechtecksfläche - aber nur dann, wenn im Intervall liegt.
Da gilt: , ist jedenfalls
.
ist aber nicht für jedes Zahlenpaar und kleiner als , da gilt:
Fallunterscheidung
Fall 1:
Fall 2:
Fall 1:
liefert lokales Maximum mit
Setze in die Nebenbedingung ein, um zu bekommen. Setze beide Werte in ein , um die maximale Fläche zu berechnen.
Das maximale Rechteck ist demnach ein Quadrat mit der Seitenlänge .
Für die Fläche gilt:
Fall 2:
Damit liegt der Scheitelpunkt der Parabel rechts vom Intervall und nimmt in diesem Intervall streng monoton zu.
Die größte Fläche wird demnach - als Randextremum - angenommen, wenn der erzeugende Punkt mit dem rechten Randpunkt zusammenfällt. Also für .
Damit gilt für die Seitenlängen des gesuchten maximalen Rechtecks und .
Die maximale Fläche ist:
Die beiden folgenden Grafiken veranschaulichen die alternative Lösung der Aufgabe.
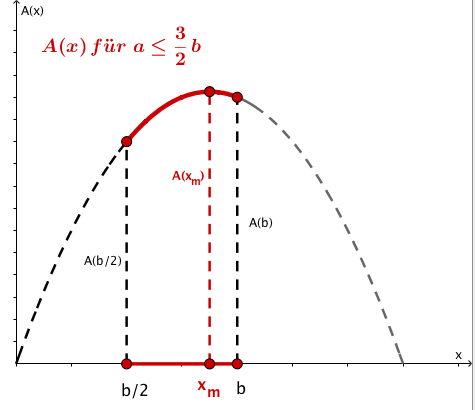
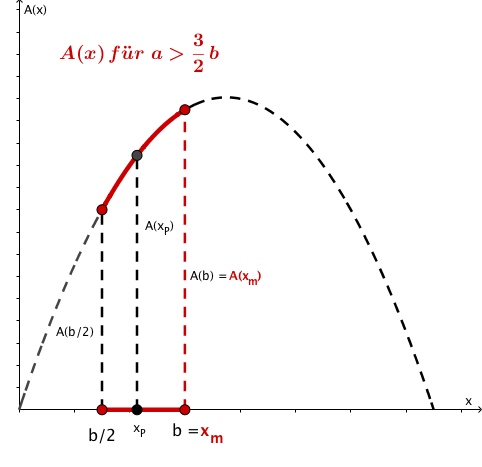
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Günther Rasch → Was bedeutet das?
