1 Übersicht
In diesem Kurs lernst du die verschiedenen Strahlensätze kennen und wie du sie anwenden kannst.
Außerdem zeigen wir dir, welche Anwendungen die Strahlensätze haben, etwa wie du (fast) ohne Hilfsmittel die Höhe von Bäume vermessen kannst.
Voraussetzungen:
Du weißt was eine zentrische Streckung ist und kannst sie bei Dreiecken anwenden
Du hast Basiswissen über Bruchgleichungen und kannst diese lösen
Du kennst die mathematische Darstellung von Strecken
Ziele:
Du weißt, wann man die Strahlensätze anwenden kann
Du kannst die Strahlensätze formulieren
Du kannst die Strahlensätze richtig anwenden
Du erkennst den praktischen Nutzen der Strahlensätze
Kursdauer
Die Bearbeitung des Kurses inklusive den Aufgaben Teil 2 dauert etwa 60 Minuten.
Die Herausforderung stellt eine sehr schwere Aufgabe dar und geht über den Anforderungen des Kurses hinaus.
2 Motivation

Stell dir vor du bist draußen unterwegs und triffst auf einen Baum. Du hast nichts dabei außer einen Meterstab und möchtest die Höhe des Baumes bestimmen.
Wie könnte das funktionieren?
3 Strahlensatz an der V-Figur
Um die Höhe eines Baumes berechnen zu können, müssen wir zunächst die Strahlensätze kennenlernen.
Grundsätzlich lassen sich die Strahlensätze bei zwei Arten von Figuren anwenden, bei sogenannten "Figuren" und "Figuren".
Betrachte das folgende Applet, um zu erfahren, wie der Strahlensatz an der Figur funktioniert.
Falls das Applet nicht richtig angezeigt wird, kannst du es unter diesem Link aufrufen: Zum Applet
4 Strahlensatz an der X-Figur
Betrachte nun das folgende Applet um zu erfahren, wie der Strahlensatz an der -Figur funktioniert.
Falls das Applet nicht richtig angezeigt wird, kannst du es unter diesem Link aufrufen: Zum Applet
5 Voraussetzungen für den Strahlensatz
In der Realität sehen die Figuren oft anders aus. Meist hat man es mit Geraden oder Halbgeraden und nicht (nur) mit Strecken zu tun.
Der Trick ist, sich diese in diesen Figuren ein geeignetes bzw. zu suchen.
Um die Strahlensätze anwenden zu können, müssen zunächst zwei wichtige Voraussetzungen erfüllt sein.
1. Voraussetzung
Zwei beliebige Geraden schneiden sich in einem Punkt (hier ).
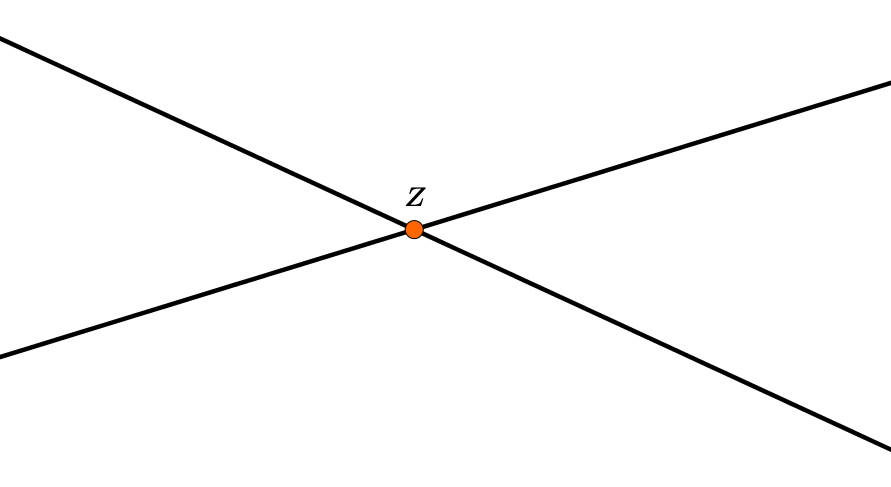
2. Voraussetzung
Diese beiden Geraden werden von zwei parallelen Geraden geschnitten, welche nicht durch den Schnittpuntk verlaufen.
Die beiden Parallelen verlaufen entweder
Beide auf einer Seite von :
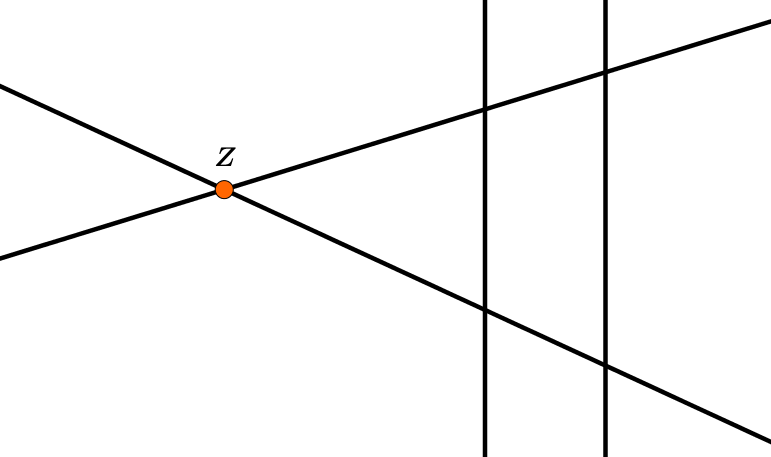
Auf je einer Seite von :
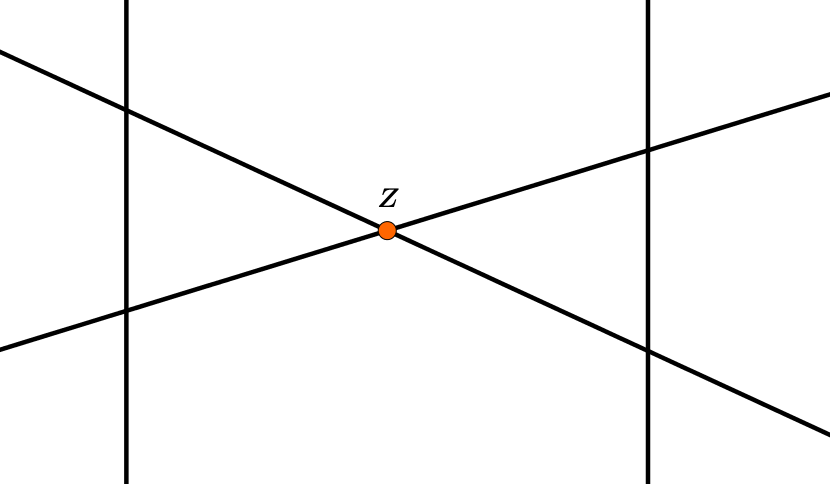
Sind diese Voraussetzungen erfüllt, kann man sich die bereits bekannten Figuren erschließen:
-Figur
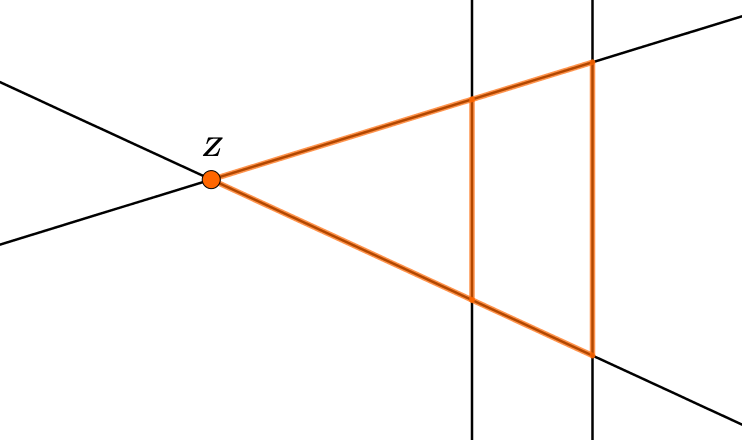
-Figur
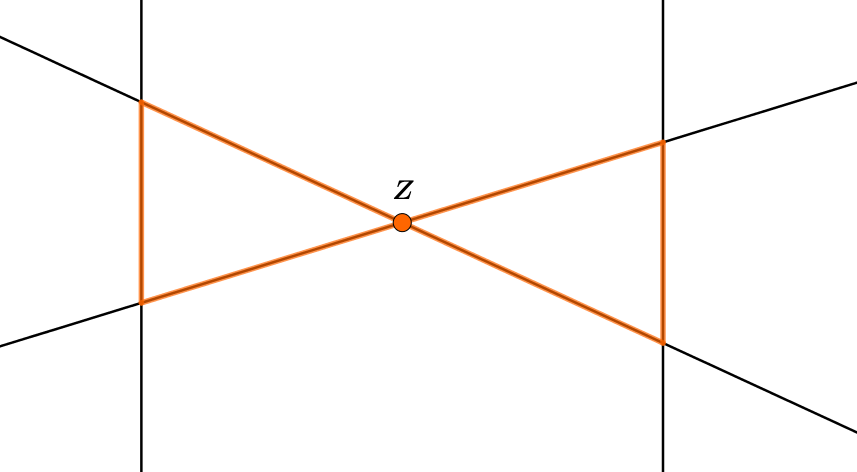
6 Zusammenfassung
Strahlensatz
Werden zwei Geraden, die sich in einem Punkt schneiden, von zwei Parallelen geschnitten (Schnittpunkte ), so verhalten sich…
…die Strecken auf der einen Geraden wie die entsprechenden Strecken auf der anderen Geraden.
…die Strecken auf den Parallelen wie die von aus gemessenen entsprechenden Strecken auf den Geraden.
-Figur
1. Strahlensatz
und
2. Strahlensatz
und
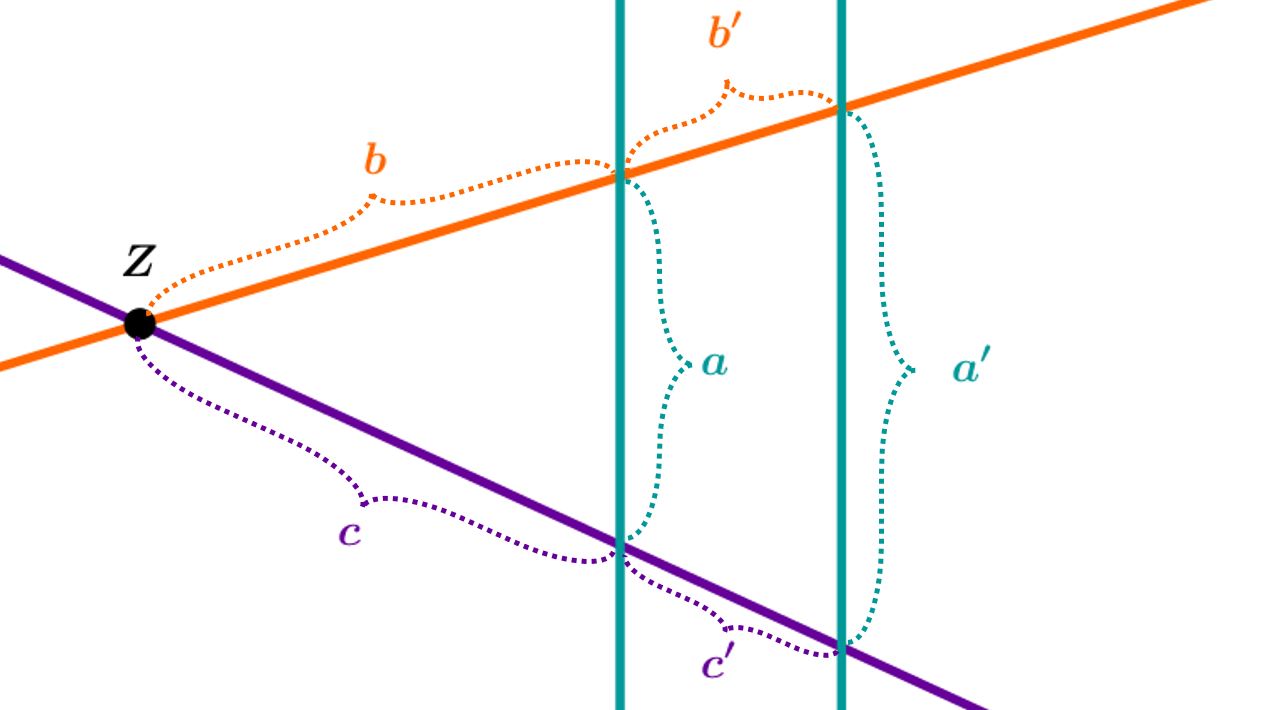
-Figur
1. Strahlensatz
und
2. Strahlensatz
und
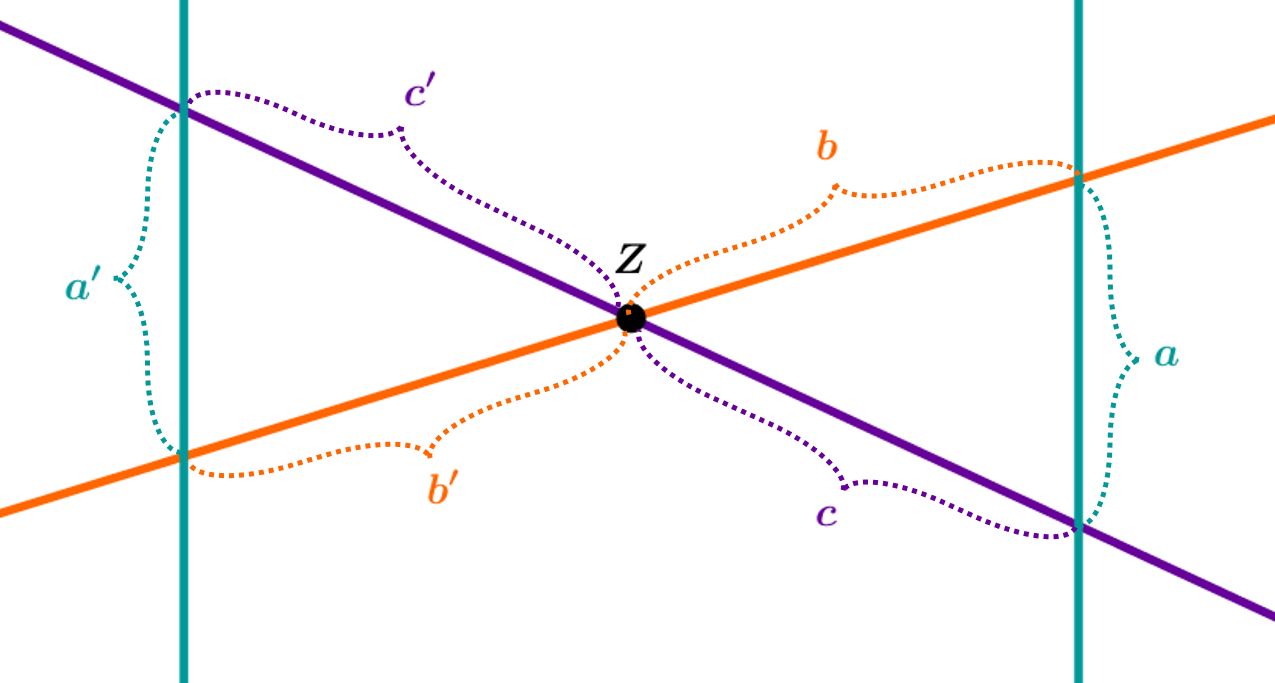
Merke:
Bei allen Verhältnissen der Strahlensätze gelten jeweils auch die Kehrbrüche!
Beispiel: Es gilt sowohl als auch
Dies kann bei manchen Umformungen von Vorteil sein.
Vorsicht: Es gilt jedoch nicht:
7 Aufgaben Teil 1
Nun ist es an dir einige Aufgaben mit dem Strahlensatz selbstständig zu lösen.
Wenn du dabei Probleme hast, schau dir die Lösung Schritt für Schritt an. Die Lösung ist sehr kleinschrittig, sodass du sie gut nachvollziehen kannst.
Aufgabe 1
Laden
Aufgabe 2
Laden
Aufgabe 3
Laden
Aufgabe 4
Laden
Aufgabe 5
Laden
8 Die Baumhöhe
Wie aber lässt sich nun die Baumhöhe mit Hilfe eines Meterstabs berechnen?

Der Mann im Bild macht es vor. Der Meterstab wird zu einem Dreieck mit rechtem Winkel "gefaltet" und dann peilt er den höchsten Punkt des Baumes über die obere Ecke des Dreiecks an.

Kannst du dir nun vorstellen, wie du mithilfe der abgelesenen Werte am Meterstab und dem Strahlensatz den Baum berechnen kannst?
Hierzu eine Skizze, mit allen benötigten Größen:
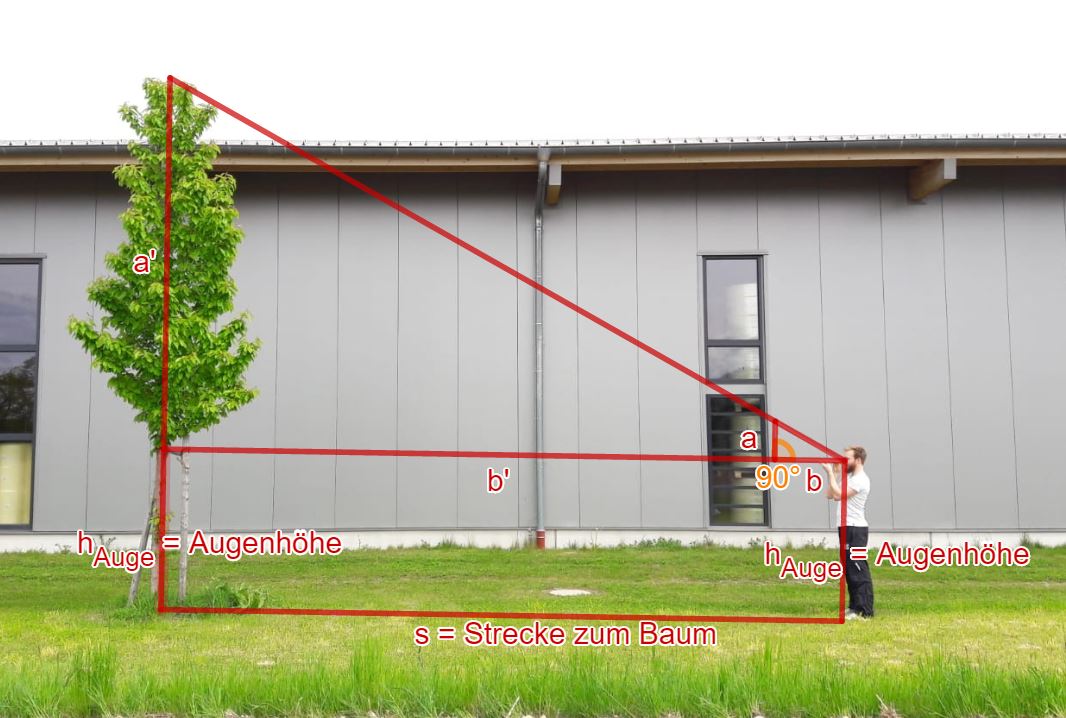
Versuche nun selbst, die Höhe des Baumes zu berechnen. Hier die gemessenen Größen im Bild:
Letztlich musst du also nur die Maße an deinem Dreieck ablesen und vom Baum aus so lange rückwärts gehen (und deine Schritte bzw. Meter zählen), bis du in Verlängerung deines Dreiecks die Spitze des Baumes siehst (siehe Bild ).
Der Rest ist "einfache" Mathematik.
Dies wird tatsächlich heute noch praktiziert. Förster benutzen dafür ein sogenanntes "Försterdreieck". Du kannst selbst recherchieren, wie dies aussieht.
9 Aufgaben Teil 2
Aufgabe 1
Laden
Aufgabe 2
Laden
10 Herausforderung
Diese Aufgabe geht über die Anforderungen des Kapitels hinaus. Falls du jedoch jemand bist, der gerne länger knobelt oder es einfach etwas anspruchsvoller mag, probiere die folgende Aufgabe.
Aufgabe 1
Laden
