Strecke

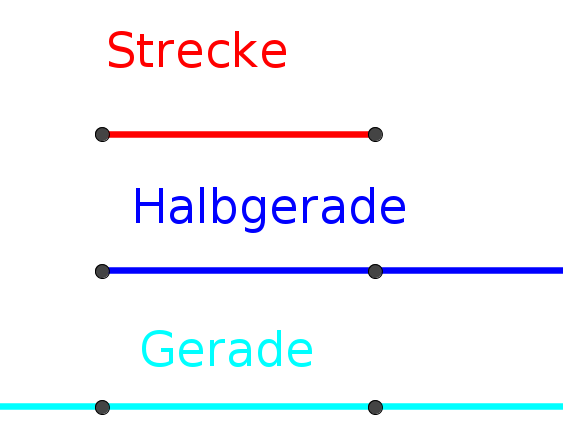
Zusammenhang von Gerade und Strecke

Betrachtet man eine Gerade $g$ und die zwei auf ihr liegenden Punkte $A$ und $B$, so ist die Strecke $[AB]$ der Teil der Geraden, der zwischen den beiden Punkten liegt. Damit ist eine Strecke durch die ihre beiden Endpunkte beschränkt, anders als die Gerade, die in beide Richtungen unendlich weiterläuft.

Mittelpunkt einer Strecke

Mittelpunkt einer Strecke konstruieren

Um den Mittelpunkt einer Strecke zu konstruieren, brauchst du nur ihre Mittelsenkrechte zu konstruieren.

Mittelpunkt einer Strecke berechnen

Wenn du die Koordinaten des Anfangspunkts $A(x_A|y_A)$ und des Endpunkts $B(x_B|y_B)$ einer Strecke gegeben hast, kannst du den Mittelpunkt wie folgt berechnen:

Abstand

Die Länge der Strecke $[AB]$ bezeichnet man mit $\overline{AB}$. $\overline{AB}$ ist der Abstand $d(A,B)$ zwischen den Punkten $A$ und $B$.

Euklidischer Abstand

Befindet man sich im kartesischen Koordinatensystem, wird der Abstand $d(A,B)$ über den Satz des Pythagoras berechnet.

Dies funktioniert bildlich wie folgt:

Die $x$-Komponente vom Punkt $B$ wird von der $x$-Komponente des Punktes $A$ abgezogen, dies wird auch mit den $y$-Komponenten gemacht. Die beiden resultierenden Werte sind die Längen der Katheten eines rechtwinkligen Dreiecks, die fehlende Seite ist die gesuchte Entfernung der Punkte, welche nun sehr leicht über den Satz des Pythagoras ausgerechnet werden kann.

Hier findest du eine noch genauere Erklärung zum Thema:

Berechnung des Abstandes zwischen zwei Punkten