Abstand zweier Punkte berechnen

Zwei verschiedene Punkte spannen eine Distanz auf, welche sowohl im Zweidimensionalen als auch im Dreidimensionalen berechnet werden kann.

Die Formeln zur Berechnung des Abstandes basieren auf dem Satz des Pythagoras.

Im Zweidimensionalen

Für $2$ Punkte $P_1\left(x_1\vert y_1\right)$ , $P_2\left(x_2\vert y_2\right)$ kann man den Abstand $d$ (distance) folgendermaßen berechnen:

\displaystyle d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

Im Dreidimensionalen

Analog zur Formel im zweidimensionalen Raum kann man den Abstand $d$ (distance) zweier Punkte $P_1\left(x_1\vert y_1\vert z_1\right),\;P_2\left(x_2\vert y_2\vert z_2\right)$ im dreidimensionalen Raum folgendermaßen berechnen:

\displaystyle d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

Vorgehen am Beispiel

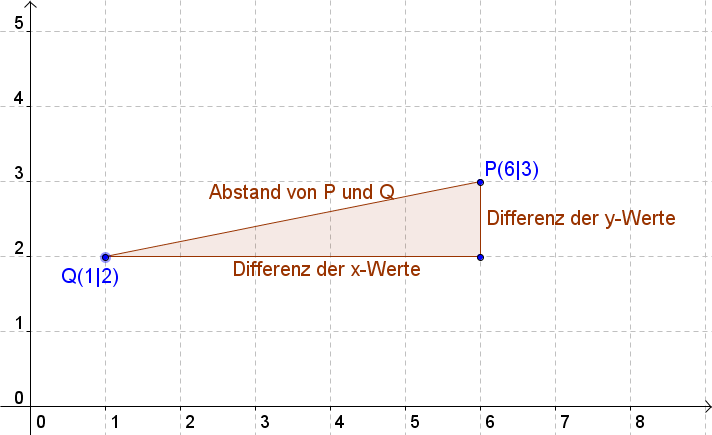
Geogebra File: https://assets.serlo.org/legacy/1024.xml

Gegeben sind die beiden Punkte $P(6|3)$ und $Q(1|2)$ , deren Abstand ermittelt werden soll.

Dazu wird ein rechtwinkliges Dreieck gebildet mit …

der Strecke zwischen den Punkten als Hypotenuse,
der Differenz der x-Werte $\left(6-1=5\right)$ als erste Kathete,
und der Differenz der y-Werte $\left(3-2=1\right)$ als zweite Kathete.

Der Abstand der Punkte (die Hypotenuse $d$ ) kann nun mit dem Satz des Pythagoras berechnet werden:

$\displaystyle d^2$	$=$	$\displaystyle (6-1)^2+(3-2)^2$
	$=$	$\displaystyle 5^2+1^2$
	$=$	$\displaystyle 26$	$\displaystyle \sqrt{}$
$\displaystyle d$	$≈$	$\displaystyle 5{,}099$

$\Longrightarrow$ Der Abstand der Punkte P und Q beträgt ungefähr $5{,}099$ .

Spezialfall: Die Punkte liegen aufeinander

Gegeben sind zwei aufeinanderliegende Punkte $P$ und $P'$ mit identischen Koordinaten $P\;(x\vert y)\;=P'(x|y)$

Der Abstand zwischen $P$ und $P'$ berechnet sich mit der Formel

\displaystyle d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

Setzt man nun die Koordinaten ein, so erhält man wegen $x_1=x_2=x$ und $y_1=y_2=y$ für den Abstand $d$ :

\displaystyle d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}

Übungsaufgaben: Abstand zweier Punkte berechnen

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Abstand

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?