Geometrie, Teil B, Aufgabengruppe 1

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

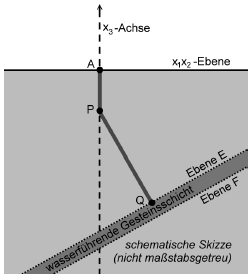
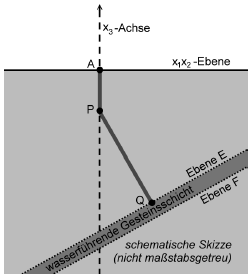
Eine Geothermieanlage fördert durch einen Bohrkanal heißes Wasser aus einer wasserführenden Gesteinsschicht an die Erdoberfläche. In einem Modell entspricht die $x_1x_2$ -Ebene eines kartesischen Koordinatensystems der horizontalen Erdoberfläche. Eine Längeneinheit im Koordinatensystem entspricht einem Kilometer in der Realität. Der Bohrkanal besteht aus zwei Abschnitten, die im Modell vereinfacht durch die Strecken $[AP]$ und $[PQ]$ mit den Punkten $A(0|0|0)$ , $P(0|0|-1)$ und $Q(1|1|-3{,}5)$ beschrieben werden (vgl. Abbildung).

(2 BE)

Berechnen Sie auf der Grundlage des Modells die Gesamtlänge des Bohrkanals auf Meter gerundet.

(3 BE)

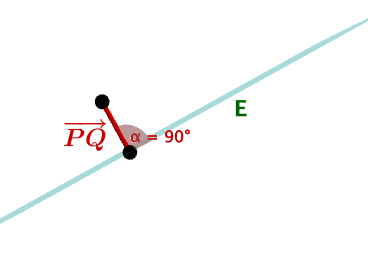
Beim Übergang zwischen den beiden Abschnitten des Bohrkanals muss die Bohrrichtung um den Winkel geändert werden, der im Modell durch den Schnittwinkel der beiden Geraden $AP$ und $PQ$ beschrieben wird. Bestimmen Sie die Größe dieses Winkels.

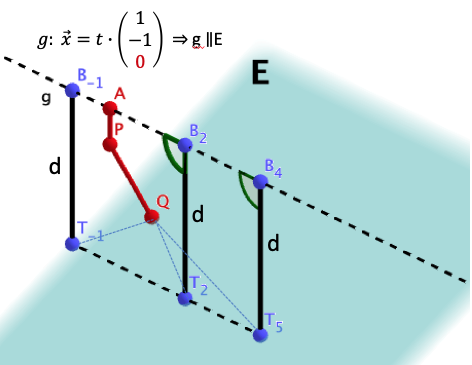
Im Modell liegt die obere Begrenzungsfläche der wasserführenden Gesteinsschicht in der Ebene $E$ und die untere Begrenzungsfläche in einer zu $E$ parallelen Ebene $F$ . Die Ebene $E$ enthält den Punkt $Q$ . Die Strecke $[PQ]$ steht senkrecht auf der Ebene $E$ (vgl. Abbildung).

(2 BE)

Bestimmen Sie eine Gleichung der Ebene $E$ in Normalenform.

(zur Kontrolle: $E:4x_1+4x_2-10x_3-43=0$ )

(6 BE)

Der Bohrkanal wird geradlinig verlängert und verlässt die wasserführende Gesteinsschicht in einer Tiefe von 3600 m unter der Erdoberfläche. Die Austrittsstelle wird im Modell als Punkt R auf der Geraden PQ beschrieben. Bestimmen Sie die Koordinaten von R und ermitteln Sie die Dicke der wasserführenden Gesteinsschicht auf Meter gerundet.

(zur Kontrolle: $x_1-$ und $x_2$ -Koordinate von R: 1,04)

Ein zweiter Bohrkanal wird benötigt, durch den das entnommene Wasser abgekühlt zurück in die wasserführende Gesteinsschicht geleitet wird. Der Bohrkanal soll geradlinig und senkrecht zur Erdoberfläche verlaufen. Für den Beginn des Bohrkanals an der Erdoberfläche kommen nur Bohrstellen in Betracht, die im Modell durch einen Punkt $B(t|-t|0)$ mit $t\,\in\,\mathbb{R}$ beschrieben werden können.

(3 BE)

Zeigen Sie rechnerisch, dass der zweite Bohrkanal die wasserführende Gesteinsschicht im Modell im Punkt $T(t|-t|-4{,}3)$ erreicht, und erläutern Sie, wie die Länge des zweiten Bohrkanals bis zur wasserführenden Gesteinsschicht von der Lage der zugehörigen Bohrstelle beeinflusst wird.

(4 BE)

Aus energetischen Gründen soll der Abstand der beiden Stellen, an denen die beiden Bohrkanäle auf die wasserführende Gesteinsschicht treffen, mindestens $1500\,m$ betragen. Entscheiden Sie auf der Grundlage des Modells, ob diese Bedingung für jeden möglichen zweiten Bohrkanal erfüllt wird.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Normalengleichung

Im Rahmen der Modellierung einer Geothermieanlage sind Normalengleichungen von Ebenen und Längen- und Winkelbestimmungen im $\mathbb{R^3}$ bedeutsam.

Der Bohrkanal setzt sich zusammen aus den Strecken $[AP]$ und $[PQ]$ mit

$A(0|0|0)$ ,

$P(0|0|-1)$ ,

$Q(1|1|-3{,}5)$ .

$1\,LE$ im Koordinatensystem entspricht $1000\,m$ in der Realität.

a)

(2 BE)

Für die Gesamtlänge $l$ des Bohrkanals gilt:

$\def\arraystretch{1.25} \begin{array}{rcll}l&=&|\overrightarrow{AP}|\,LE\,+|\overrightarrow{PQ}|\,LE\,\\&=&\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\right|\,LE\,+|\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}|\,LE\\&=&1\,LE\,+\sqrt{1^2+1^2+(-2{,}5)^2}LE\\&\approx&1\,LE\;+\quad2{,}8723\,LE\\&\approx&3{,}8723\;LE\end{array}$

Länge in der Realität:

$l\approx 3{,}8723\cdot 1000\,m=3872{,}3\,m$

Ergebnis:

Die Gesamtlänge des Bohrkanals beträgt rund $3872\,m$ .

b)

(3 BE)

Für den spitzen Schnittwinkel $\varphi$ der beiden Geraden $AP$ und $PQ$ gilt:

$cos\,\varphi=\displaystyle \frac{|\overrightarrow{AP}\circ\overrightarrow{PQ}|}{|\overrightarrow{AP}|\cdot |\overrightarrow{PQ}|}$

Setze die Komponenten der Vektoren ein:

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

$\displaystyle cos\, \varphi$	$=$	$\displaystyle \displaystyle \frac{2{,}5}{\sqrt{8{,}25}}$
	$≈$	$\displaystyle 0{,}3704$	$\displaystyle cos^{-1}$
$\displaystyle \varphi$	$≈$	$\displaystyle 29{,}5°$

Ergebnis:

Die Bohrrichtung muss um den Winkel von etwa $29{,}5°$ geändert werden.

c)

(2 BE)

Wenn die Strecke $[PQ]$ auf der Ebene $E$ senkrecht steht, ist der Vektor $\overrightarrow{PQ}$ Normalenvektor von $E$ .

Ansatz für die Ebene $E$ in Vektorform:

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

Skalarprodukt bilden:

$E:\;1\cdot (x_1-1)+1\cdot (x_2-1)-2{,}5\cdot (x_3+3{,}5)=0$

Zusammenfassen:

$E:\;x_1+x_2-2{,}5x_3-10{,}75=0\quad|\cdot 4$

$E:\;4x_1+4x_2-10x_3-43=0$

Damit ist das angegebene Kontrollergebnis bestätigt.

Hinweis:

Die Multiplikation der Ebenengleichung auf beiden Seiten mit $4$ hat lediglich den Grund, bei der weiteren Benutzung der Ebenengleichung ganzzahlige Koeffizienten zu haben.

Alternativer Ansatz für die Ebene $E$ in Koordinatenschreibweise:

$E:ax_1+bx_2+cx_3+d =0$

Die drei Koeffizienten $a,b,c$ sind die Komponenten eines beliebigen Normalenvektors von $E$ .

Hier vom Vektor $\overrightarrow{PQ}=\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}$

Setze die Komponenten von $\overrightarrow{PQ}$ in die Ebenengleichung ein:

$E:{\color{red}1}\cdot x_1+{\color{red}1}\cdot x_2+({\color{red}-2{,}5})\cdot x_3+d=0$

Um das konstante Glied $d$ zu bestimmen, setzt du jetzt den Punkt $Q(1\vert1\vert-3{,}5)$ in $E$ ein:

$1\cdot {\color{red}1}+1\cdot {\color{red}1}-2{,}5 \cdot({\color{red}-3{,}5})+d=0$ $\quad\Rightarrow$

$d=-10{,}75$

Auch über diesen Weg erhältst du die Ebene

$E:4x_1+4x_2-10x_3-43=0$ .

d)

(6 BE)

Zum Verständnis der Abbildung der Geothermieanlage:

Die 3. Koordinaten der gegebenen Punkte $A;P;Q$ geben (in Tausendstel Meter) an, wie tief die Punkte unter der Erdoberfläche liegen.

$P$ liegt in der Realität also $1000\,m$ und $Q$ liegt $3500\,m$ unter der Erdoberfläche.

Wenn der gesuchte Punkt $R$ $\;3600\,m$ unter der Erdoberfläche liegen soll, so heißt dies, dass für die Rechnung seine 3. Koordinate den Wert $-3{,}6$ haben muss.

Du bestimmst also den Punkt $R\left(r_1|r_2|{\color{red}-3{,}6}\right)$ der Geraden $PQ$ .

Die Gleichung der Geraden $PQ$ lautet:

$PQ:\overrightarrow{x}=\overrightarrow {OP}+\lambda\cdot \overrightarrow{PQ};\;\lambda\in\mathbb{R}$

$PQ:\overrightarrow{x}=\begin{pmatrix}0\\0\\-1\end{pmatrix}+\lambda\cdot \begin{pmatrix}1\\1\\-2{,}5\end{pmatrix};\;\lambda \in \mathbb{R}$

$R(r_1|r_2|-3{,}6) \in PQ$ ergibt:

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

$\def\arraystretch{1.25} \begin{array}{rrcll}\mathrm{I}&r_1&=&\lambda\\\mathrm{II}&r_2&=&\lambda\\\mathrm{III}&-3{,}6&=&-1-2{,}5\cdot \lambda\\&2{,}5\cdot \lambda&=&2{,}6&|\,:2{,}5\\&\lambda&=&1{,}04\end{array}$

Teilergebnis:

Im Modell ist die Austrittsstelle des Bohrkanals aus der wasserführenden Schicht der Punkt $R(1{,}04|1{,}04|-3{,}6)$ .

Da die Ebenen $E$ und $F$ parallel sind, ist die Dicke der wasserführenden Schicht der Abstand der beiden Ebenen.

Und weil die Punkte $Q$ und $R$ auf einer Normalen zur Ebene liegen, kannst du auch den Abstand dieser beiden Punkte als Dicke der Schicht nehmen.

Abstand $d$ der beiden Punkte $Q$ und $R$ :

$\def\arraystretch{1.25} \begin{aligned}d(Q;r)&= \vert \overrightarrow{QR}\vert\\&=\displaystyle\left |\begin{pmatrix}1{,}04\\1{,}04\\-3{,}6\end{pmatrix}-\begin{pmatrix}1\\1\\-3{,}5\end{pmatrix}\right|\\&=\left|\begin{pmatrix}0{,}04\\0{,}04\\-0{,}1\end{pmatrix}\right|\end{aligned}$

$d(Q,R)=\displaystyle\sqrt{0{,}04^2+0{,}04^2+(-0{,}1)^2}$

$d(Q,R)\approx0{,}1149$

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

$1000\,m\cdot 0{,}1149\approx115\,m$

Ergebnis:

Die Dicke der wasserführenden Gesteinsschicht beträgt rund $115\,m$ .

Alternative Berechnung der Dicke der wasserführenden Schicht über die Hesse-Normalform der Ebene $E$ :

Setze den Punkt $R$ in die HNF von $E$ ein. Das Ergebnis ist die gesuchte Dicke $d$ .

HNF von $E$ :

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

$\def\arraystretch{1.25} \begin{array}{rcll}d(\mathrm{R};\mathrm{E})&=&\displaystyle \frac{4\cdot {\color{red}1{,}04}+4\cdot {\color{red}1{,}04}-10\cdot ({\color{red}-3{,}6})-43}{\sqrt{132}}\\&=&\displaystyle \frac{8\cdot 1{,}04-7}{\sqrt{132}}\\&\approx&0{,}115\end{array}$

e)

(3 BE)

Die möglichen Bohrstellen sind die Punkte $B(t|-t|0)$ mit $t\in\mathbb{R}$ .

Ein Richtungsvektor eines Bohrkanals ist, da dieser senkrecht zur Erdoberfläche verlaufen soll, zum Beispiel der Vektor $\,\begin{pmatrix}0\\0\\1\end{pmatrix}$ .

Ein (möglicher) Kanal wird also durch folgende Gerade $k$ modelliert:

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

Bestimme den Schnittpunkt von $k$ mit der Ebene $E$ , indem du $x_1=t$ und $x_2=-t$ und $x_3=\lambda$ in die Normalenform der Ebene

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

einsetzt und die Gleichung nach $\lambda$ auflöst.

$\def\arraystretch{1.25} \begin{array}{rcrl}4t-4t-10\lambda-43&=&0&|\;+43\\-10\lambda&=&43&|\;:(-10)\\\lambda&=&-4{,}3\end{array}$

Ergebnis

Ausgehend von einem Bohrpunkt $B(t|-t|0)$ erreicht der zweite Bohrkanal die wasserführende Schicht im Modell im Punkt $T(t|-t|-4{,}3)$ .

Für jeden Bohrpunkt $B$ misst die 3. Koordinate von $T$ die Länge des Bohrkanals, da dieser senkrecht zur $x_1$ - $x_2$ -Ebene verläuft.

Die Länge eines jeden zweiten Bohrkanals beträgt also in der Realität $4300\,m$ und ist unabhängig von der Lage der Bohrstelle.

Veranschaulichung des Modells mit einer räumlichen Skizze

Die möglichen Bohrstellen $B(t|-t|0)$ liegen in der $x_1$ - $x_2$ -Ebene auf der Geraden

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

Diese Gerade $g$ ist zur Ebene $E$ parallel, da ihr Richtungsvektor senkrecht zum Normalenvektor von $E$ ist:

\displaystyle \def\arraystretch{1.25} \begin{array}{l}\\\cos\;\varphi=\frac{\left|\begin{pmatrix}0\\0\\-1\end{pmatrix}\;\circ\;\begin{pmatrix}1\\1\\-2{,}5\end{pmatrix}\right|}{\begin{vmatrix}0\\0\\-1\end{vmatrix}\cdot\begin{vmatrix}1\\1\\-2{,}5\end{vmatrix}}=\frac{2{,}5}{1\cdot\sqrt{1^2+1^2+(-2{,}5)^2}}\end{array}

Somit erreichen alle möglichen Bohrkanäle die Ebene $E$ in der gleichen Tiefe $d$ .

f)

(4 BE)

Aus der obenstehenden Skizze entnimmst du, dass zu überprüfen ist, ob für jedes $t \in \mathbb{R}$ der Abstand des jeweiligen Punkts $T(t|-t|-4{,}3)$ vom Punkt $Q(1|1|-3{,}5)$ im Modell mindestens $1{,}5\,LE$ beträgt.

Es gilt:

$\def\arraystretch{1.25} \begin{array}{rcll}\overline{TQ}&=&\left|\begin{pmatrix}t\\-t\\-4{,}3\end{pmatrix}-\begin{pmatrix}1\\1\\-3{,}5\end{pmatrix}\right|\\&=&\left|\begin{pmatrix}1-t\\1+t\\0{,}8\end{pmatrix}\right|\\&=&\sqrt{(1-t)^2+(1+t)^2+0{,}8^2}\\&=&\sqrt{2t^2+2{,}64}\\&{\color{red}>}&\sqrt{2{,}64}\;\approx{1{,}62}\end{array}$

Ergebnis:

Die Bedingung, dass der Abstand der beiden Stellen, an denen der erste und der zweite Bohrkanal auf die wasserführende Gesteinsschicht trifft, mindestens $1500\,m$ beträgt, ist für jeden möglichen zweiten Bohrkanal erfüllt.

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?