$ax^2+4x+4=2x+3$

Forme die quadratische Gleichung so um, dass auf einer Seite die Null steht, und fasse so weit wie möglich zusammen.

$ax^2+2x+1=0$

Lies die Werte der Koeffizienten $a$, $b$ und $c$ ab. Beachte, dass das $a$ auf der linken Seite dem $a$ aus der allgemeinen Form entspricht.

$a=a,\;b=2,\;c=1$

Im Sonderfall $a=0$ fällt der Term mit $x^2$ weg und es ergibt sich eine lineare Gleichung. Diesen Fall betrachtest du unten gesondert.

Sei nun $\mathbf a\neq\mathbf0$:

Berechne die Diskriminante $D=b^2-4ac$ der Gleichung.

$D=2^2-4\cdot a\cdot1=4-4a=4(1-a)$

Überprüfe die Diskriminante in Abhängigkeit von $a$ auf ihr Vorzeichen, indem du sie gleich Null setzt.

$D=4(1-a)=0\Leftrightarrow a=1$

Du kannst $1-a$ als eine Gerade mit negativer Steigung betrachten und so das Vorzeichenverhalten der Diskriminante bestimmen. Dadurch erhältst du eine Aussage über die Anzahl der Lösungen.

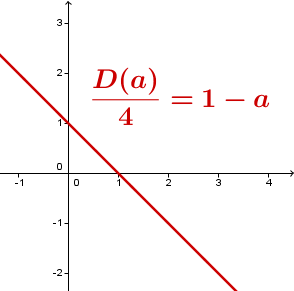
Dabei ist $a=0$ ein Spezielfall, den du getrennt betrachten musst.

$a<1\;\Rightarrow\;D>0\;\Rightarrow$

$a=1\;\Rightarrow\;D=0\;\Rightarrow$

$a>1\;\Rightarrow\;D<0\;\Rightarrow$

$a=1\;\Rightarrow$

zwei Lösungen

eine Lösungen

keine Lösung

Spezialfall

Wende die nun Mitternachtsformel an.

$a<1:\:x_{1{,}2}=\frac{-2\pm\sqrt{4(1-a)}}{2a}=\frac{-1\pm\sqrt{1-a}}a$

$a=1:\:x=\frac{-2\pm0}{2\cdot1}=-1$

$a>1:\;keine\;Lösung$

Sei nun $\boldsymbol a\boldsymbol=\mathbf0$:

In diesem Fall fällt der Term mit $x^2$ weg und es ergibt sich eine lineare Gleichung.

Diese kannst du durch Äquivalenzumformung lösen.

$\def\arraystretch{1.25} \begin{array}{l}\begin{array}{ccc}0\cdot x^2+2x+1&=&0\\2x+1&=&0\\x&=&-\frac12\end{array}\end{array}$