1 Übersicht
In diesem Kurs lernst du Potenzen mit negativen Exponenten kennen und wie man mit Potenzen rechnet (Potenzgesetze).
Außerdem lernst du, wie man sehr große (z. B. ) oder sehr kleine Zahlen (z. B. ) übersichtlicher darstellen kann.
Voraussetzungen
Du kennst die Darstellung von Potenzen mit natürlichen Exponenten
Du kannst Terme zusammenfassen
Du weißt, wie man mit Dezimalzahlen rechnet
Ziele
Du kennst die Darstellung von Zahlen mit negativen Exponenten
Du kennst die Potenzgesetze und kannst sie anwenden
Du kannst mit der wissenschaftlichen Schreibweise von Zahlen umgehen
Kursdauer
Die Bearbeitung des Kurses dauert etwa 90 Minuten.
2 Motivation
Atome sind überall
Ein Heliumatom besitzt einen Durchmesser von etwa Meter, ein Wasserstoffatom wiegt etwa Kilogramm.

Wie sind diese Angaben zu deuten? Welche Vorstellung können wir uns von der Größe und der Masse dieser Atome machen?
Die Masse des Jupiters beträgt etwa kg, wovon etwa kg Wasserstoff sind.

Zehnerpotenzen (mit natürlichen Zahlen im Exponenten) kennst du schon seit einigen Jahren. Sie dienen dazu, enorm große Zahlen zu veranschaulichen.
Die Frage ist: kannst du ohne Taschenrechner bestimmen, wie viele Wasserstoffatome Jupiter enthält?
3 Wiederholung
Potenzen mit natürlichen Exponenten kennst du bereits, z.B.:
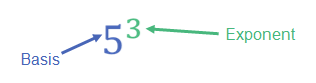
Du weißt auch, wie man grundsätzlich mit Potenzen rechnet.
Der Exponent gibt also an, wie oft die Basis als Faktor auftritt.
Bearbeite die folgenden Aufgaben, um dein Grundwissen wieder aufzufrischen.
Laden
4 Potenzen mit gleicher Basis
Hier im Beispiel siehst du Potenzen mit der Basis 4. Die Exponenten unterscheiden sich allerdings.
Überlege dir nun, wie man von der obersten Zeile zur zweitobersten Zeile kommt. Von der zweitobersten zur zweituntersten und von dort zur untersten.
Welche Rechenoperation muss man durchführen?
5 Negative Exponenten
In dem folgenden Video wird erklärt, wie man von einer Zeile zur nächsten kommt - und vor allem, wie es weitergeht.
Du siehst also: Bei negativen Exponenten entsteht ein Bruch.
Im Zähler steht immer die 1, im Nenner steht die Basis und der Exponent :
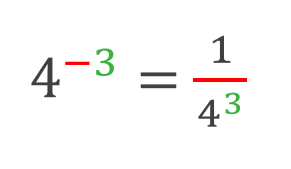
6 Erster Zwischenstand
Die bisherigen Erkenntnisse zu Potenzen werden hier nochmal zusammengefasst
für jede rationale Zahl a und jede natürliche Zahl n
für jede rationale Zahl a
für jede rationale Zahl a mit
für jede rationale Zahl a mit und jede natürliche Zahl
Klammern werden zuerst ausgerechnet. Ansonsten wird zunächst die Potenz und dann Punkt vor Strich gerechnet. Das ist vor allem bei negativen Zahlen in der Basis wichtig!
aber
Versuche nun, die folgenden Aufgaben zu lösen.
Laden
7 Übungsaufgaben 1
Teste hier dein neu gelerntes Wissen!
Laden
Laden
Laden
8 Große und kleine Zahlen
Besondere Bedeutung haben Potenzen und negative Potenzen bei der Basis 10. Dort werden Potenzen genutzt, um große oder kleine Zahlen abzukürzen.
Zehnerpotenzen mit positiven Exponenten
Diese kennst du bereits. Eine Million ist beispielsweise:
Zehnerpotenzen mit negativen Exponenten
Schreibt man die 10 mit einem negativen Exponenten, erhält man Folgendes:
Ein Zehntel kann man direkt als Dezimalbruch schreiben.
Die 1 steht nun an der ersten Stelle hinter dem Komma.
Ein Tausendstel kann man auch direkt in einen Dezimalbruch verwandeln.
Die 1 steht nun an der dritten Stelle hinter dem Komma.
Merke: Die 1 steht also immer an der Stelle hinter dem Komma, die dem Betrag des Exponenten entspricht (z.B. im zweiten Beispiel oben an der dritten Stelle, weil die Potenz den Betrag 3 besitzt).
Beispiele
Wir können nun umgekehrt Zahlen direkt in Zehnerpotenzen umwandeln:
Auf diese Art und Weise werden viele Zahlen zum Beispiel in der Physik angegeben, um einfacher mit ihnen rechnen zu können.
Bearbeite nun die folgenden Aufgaben, um zu sehen, ob du es verstanden hast.
Laden
Laden
9 Rechnen mit Potenzen mit gleicher Basis
Beim Rechnen mit Potenzen gibt es einige Rechenregeln. Betrachten wir zunächst Potenzen mit gleicher Basis:
Multiplikation von Potenzen
Man rechnet als Ergebnis als Exponent. Allgemein kann man schreiben:
Division von Potenzen
Man rechnet als Ergebnis als Exponent. Allgemein kann man schreiben:
Addition und Subtraktion von Potenzen
Bei der Addition und Subtraktion kann man keine Vereinfachung machen.
Beispielsweise lässt sich nicht vereinfachen.
10 Zusammenfassung
Negative Exponenten und Potenzgesetze
Definition
für Beispiel:
für Beispiel:
für Beispiel:
für Beispiele:
Beachte: aber
Große und kleine Zahlen in wissenschaftlicher Schreibweise
10 mit positivem Exponentendas Komma rückt um 7 Stellen nach rechts
10 mit negativen Exponentendas Komma rückt um 4 Stellen nach links
Rechengesetze für Potenzen und
Beispiele:
Beispiele:
11 Übungsaufgaben 2
Teste dein neu gelerntes Wissen anhand dieser Aufgaben:
Laden
Laden
12 Wasserstoffatome im Jupiter
Löse die Aufgabe der Motivation nun mit deinem neu gelernten Wissen!
Laden
