Aufgaben zu Umfängen von Figuren mit Halb- und Viertelkreisen

1
Berechne den Gesamtumfang der Figur. Die Maße kannst du dem Bild unten entnehmen. Runde dein Ergebnis auf eine Nachkommastelle.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis
Die allgemeine Formel zur Berechnung des Kreisumfangs ist:
Die Figur setzt sich aus dem blauen Kreis und dem weißen Halbkreis zusammen. Daraus folgt für den Gesamtumfang:
Vergiss nicht den Durchmesser zum Halbkreis hinzu zu addieren für die untere Linie, des Halbkreises.
Der Durchmesser $d$ der beiden Kreise ist in der Zeichnung gegeben. Für die Formel brauchst du aber den Radius $r$ . Diesen kannst du wie folgt berechnen:
Nun brauchst du nur noch die gegebenen Werte einzusetzen.
Das heißt, dass der Gesamtumfang ca. 85,7 cm beträgt.
2
Berechne den Gesamtumfang der unten dargestellten Figur.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang
Die Figur setzt sich aus mehreren Figuren zusammen.
Sie besteht aus dem hier grünen Kreis, dem blauen Halbkreis und den beiden orangen Halbkreisen. Der Umfang der Figur setzt sich aus den Umfängen der bunten Kreisteile zusammen.
Die allgemeine Formel zur Berechnung des Kreisumfangs ist:
Berechne nun die Umfänge $U_{\text{grün}}$ , $U_{\text{blau}}$ und $U_{\text{orange}}$ .
$U_{\text{grün}}$ ist der Umfang eines Kreises mit einem Radius von $1{,}5 \text{cm}$ .
$U_{\text{grün}}=2\pi \cdot 1{,}5\text{cm}\\=\pi \cdot 3\text{cm} \\\approx 3{,}14 \cdot 3\text{cm}\\=9{,}42\text{cm}$
$U_{\text{blau}}$ ist der Umfang eines Halbkreises, von dem die Längen der angrenzenden orangen Schnittlinien abgezogen werden müssen. Der Umfang des blauen Objekts besteht aus dem halben Umfang eines ganzen Kreises und der Länge der unteren Seite minus $2\cdot1\text{cm}=2\text{cm}$ . Die untere Seite ist $7\text{cm}$ lang. Das ist außerdem auch der Durchmesser des Halbkreises. Somit ist der Radius des Halbkreises $7\text{cm}:2 = 3{,}5\text{cm}$ .
$U_{\text{blau}}= \frac 12 \cdot 2\pi\cdot 3{,}5 \text{cm} + (7\text{cm}-2\text{cm})\\=\pi\cdot 3{,}5 \text{cm} + (7\text{cm}-2\text{cm})\\\approx 3{,}14\cdot 3{,}5 \text{cm} + 5\text{cm}\\=10{,}99\text{cm}+5\text{cm}\\=15{,}99\text{cm}$
$U_{\text{orange}}$ sind zwei Halbkreise mit dem gleichen Durchmesser von $1\text{cm}$ . Deren Umfang ist der gleiche wie der eines ganzen Kreises mit Durchmesser $1\text{cm}$ . Der Radius beträgt hier $0{,}5\text{cm}$ . Die obere Seite der Halbkreise müssen wir nicht berechnen, da sie an den blauen Halbkreis angrenzen.
$U_{\text{orange}}=2\pi\cdot0{,}5\text{cm}\\=\pi\cdot1\text{cm}\\\approx3{,}14\cdot 1\text{cm}\\=3{,}14\text{cm}$
Der Gesamtumfang setzt sich nun aus der Summe der Umfänge $U_\text{grün}$ , $U_\text{blau}$ und $U_\text{orange}$ zusammen.
$\def\arraystretch{1.25} \begin{array}{rcllll}U_\text{Gesamt}&=&U_\text{grün}&+U_\text{blau}&+U_\text{orange}\\&\approx&9{,}42\text{cm}&+15{,}99\text{cm}&+3{,}14\text{cm}&\\&=&28{,}55\text{cm}\end{array}$
Der Gesamtumfang der Figur beträgt in etwa $28{,}55\text{cm}$ .
3
Du siehst eine Abbildung von Pacman. Berechne den Umfang dieser Figur. Ein Kästchen entspricht dabei 0,5cm. Außerdem kannst du annehmen, dass der Mund von Pacman ein Viertel des Kreises ausmacht. Runde das Ergebnis auf 2 Nachkommastellen.
cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnung des Umfangs eines Kreises
Den Umfang eines Kreises berechnest du mit der Formel:
$U=2\cdot\pi\cdot r=d\cdot\pi$
Du kannst den Durchmesser d durch Zählen der Kästchen herausfinden Der Durchmesser ist 10 Kästchen lang, also $d=0{,}5cm\cdot10=5cm$ .
$U=d\cdot\pi=5cm\cdot\pi\approx15{,}71cm$
Um nur den Umfang von dem $\frac{3}{4}$ -Kreis zu berechnen, multiplizierst du den Umfang mit $\frac{3}{4}$ :
$U_{kreis\ pacman}=\frac{3}{4}\cdot5cm\cdot\pi=\frac{3}{4}\cdot15{,}71cm\approx11{,}78cm$
Als letzten Schritt darfst du nicht vergessen den Umfang des Mundes zu berechnen. Die obere und untere Linie entsprechen jeweils dem Radius des Kreises, also der Hälfte des Durchmessers:
$r=\frac{5cm}{2}=2{,}5cm$
Die Länge der beiden Linien rechnest du noch zum vorher berechneten Umfang dazu:
$U_{pacman}=11{,}78cm+2{,}5cm+2{,}5cm=16{,}78cm$
Der Umfang von Pacman beträgt also $16{,}78cm$ .
4
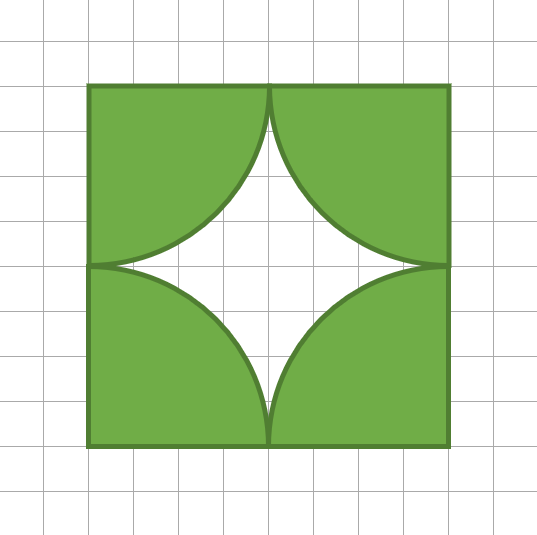
Lisa hat ein Pferd, eine Kuh, ein Schaf und einen Esel. Sie möchte jedem ein eigenes Stück Wiese zur Verfügung stellen. Dafür wird ein Zaun, um die Felder herum benötigt. Berechne wie viel Zaun Lisa braucht. Ein Kästchen in der Abbildung entspricht 10m in der Realität. Runde dein Ergebnis auf 2 Nachkommastellen.
Fällt dir ein einfacher und schneller Lösungsweg auf?
m

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnung des Umfangs eines Kreises
Den Umfang eines Kreises berechnest du mit der Formel:
$U=2⋅π⋅r=d⋅π$
Der Radius des Kreises ist 4 Kästchen lang. Das entspricht 40m. Nun kannst du den Wert in die Formel einsetzen:
$U_{Kreis}=2⋅\pi⋅r=2\cdot\pi\cdot40m=80m\cdot\pi\approx251{,}33m$
Das ist die Länge der 4 Kreisbögen. Nun musst du noch die Länge des Zauns um die 4 Felder herum berechnen. Du hast 4 gleich lange Seiten von je 8 Kästchen, also 80m:
$U_{außen}=4\cdot80m=320m$
Der Gesamtumfang ist die Summe aus dem Umfang der Kreisbögen und dem Umfang um die Felder herum.
$U_{gesamt}=U_{Kreis}+U_{außen}=251{,}33m+320m=571{,}33m$
Lisa braucht also einen Zaun mit einer Länge von 571,33m.
Da du 4 gleiche Viertelkreise hast, kannst du diese zu einem vollständigen Kreis ergänzen. Deshalb kannst du in der Aufgabe gleich den Umfang eines ganzen Kreises berechnen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?