In einer Höhe von 5000 m über Trübsalhausen ziehen dunkle Wolken auf und es fängt an zu regnen. Die Regentropfen fallen in einer Minute 500 m weit nach unten.
(a) Berechne, welche Höhe die Regentropfen nach einer, zwei bzw. fünf Minuten über dem Boden haben. Fertige daraus eine Wertetabelle an.
(b) Stelle einen Term auf, der die Höhe der Regentropfen (Einheit km) in Abhängigkeit der Fallzeit in Minuten angibt. Du kannst dabei vernachlässigen, dass die Tropfen nach der Ankunft am Boden nicht mehr weiter fallen.
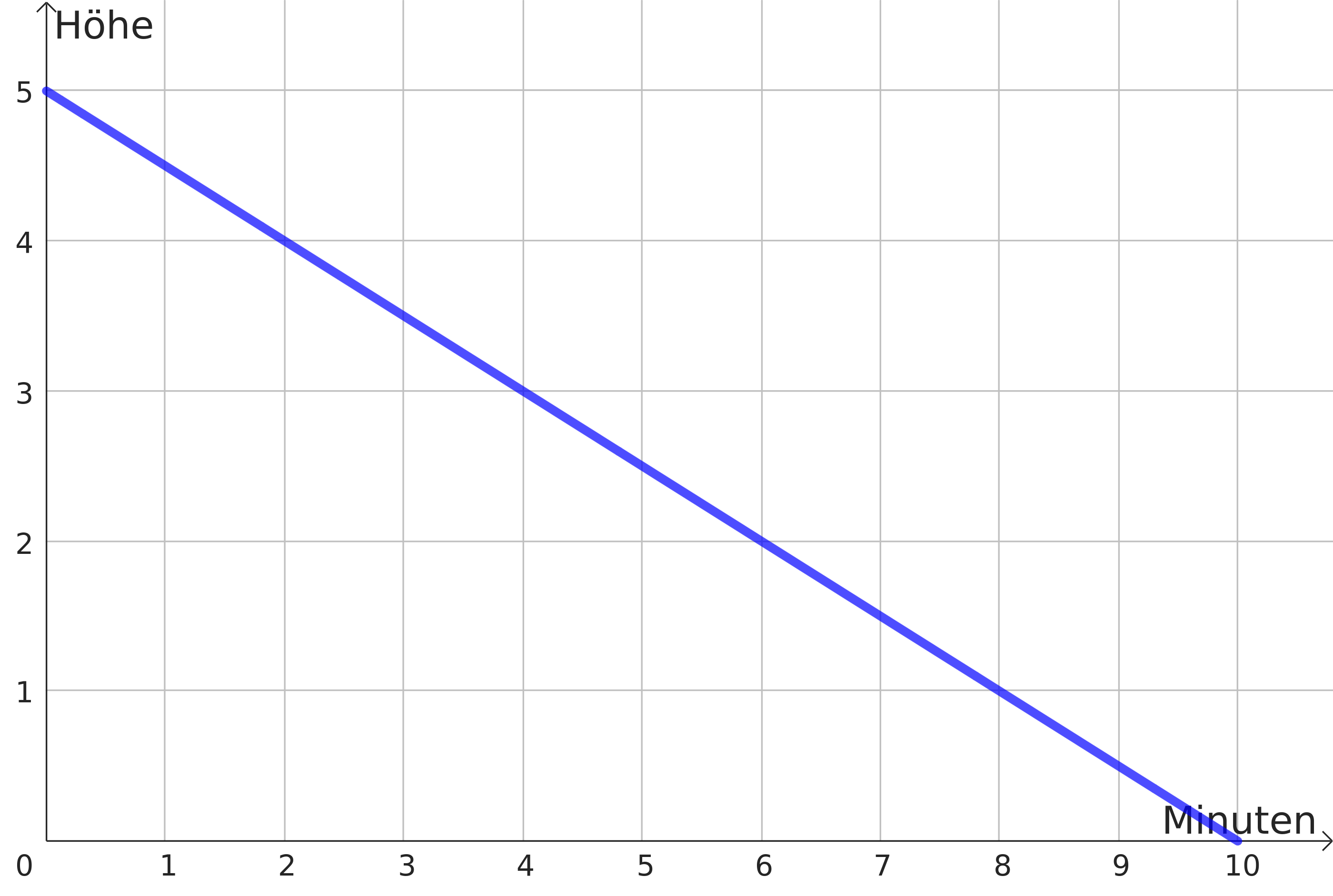
(c) Zeichne den Zusammenhang aus Teilaufgabe (b) in ein Koordinatensystem.
(d) Bestimme, nach wie vielen Minuten die Regentropfen am Boden angekommen sind.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktion
(a) Wenn ein Regentropfen in 5000 m Höhe anfängt zu fallen und er in einer Minute 500 m fällt, dann ist er nach einer Minute noch 4500 m über Trübsalhausen.
Berechnen kann man dies auch mit:
5000 m−1⋅500 m=4500 m
Für zwei Minuten ändert sich die Rechnung:
5000 m−2⋅500 m=4000 m
Nach fünf Minuten:
5000 m−5⋅500 m=1500 m
Als Wertetabelle ergibt sich:
Minuten
0
1
2
5
Höhe
5000 m
4500 m
4000 m
1500 m
(b) In Aufgabe (a) sieht man sehr gut den Unterschied in den drei Formeln. Sie unterscheiden sich nur durch die Zahl vor den 500 m. Diese Zahl ist die Veränderliche, also x. Dann kann man die Höhe eines Tropfens durch folgenden Term ermitteln.
5000 m−x⋅500 m
Da in der Aufgabenstellung aber die Einheit km verlangt wird, ist der Term:
5−x⋅0,5
die Lösung der Aufgabe.
(Hinweis: In der Aufgabenstellung wird hingewiesen, dass man vernachlässigen darf, ob der Tropfen bereits aufgekommen ist. Falls man dies nicht vernachlässigen möchte, muss man x einschränken. x darf nur größer 0 sein [der Tropfen startet mit 0 Minuten] und muss kleiner als 10 sein [bei 10 Minuten ist der Tropfen aufgekommen].)
(c)
(d) Um zu bestimmen, wann der Regentropfen am Boden ist, musst du im Graphen die Zeit ablesen, die zur Höhe 0 gehört.
Das sind 10 Minuten.
Alternativ kannst du auch ein x ermitteln, so dass sich die Höhe 0 ergibt:
