Analysis, Teil A, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
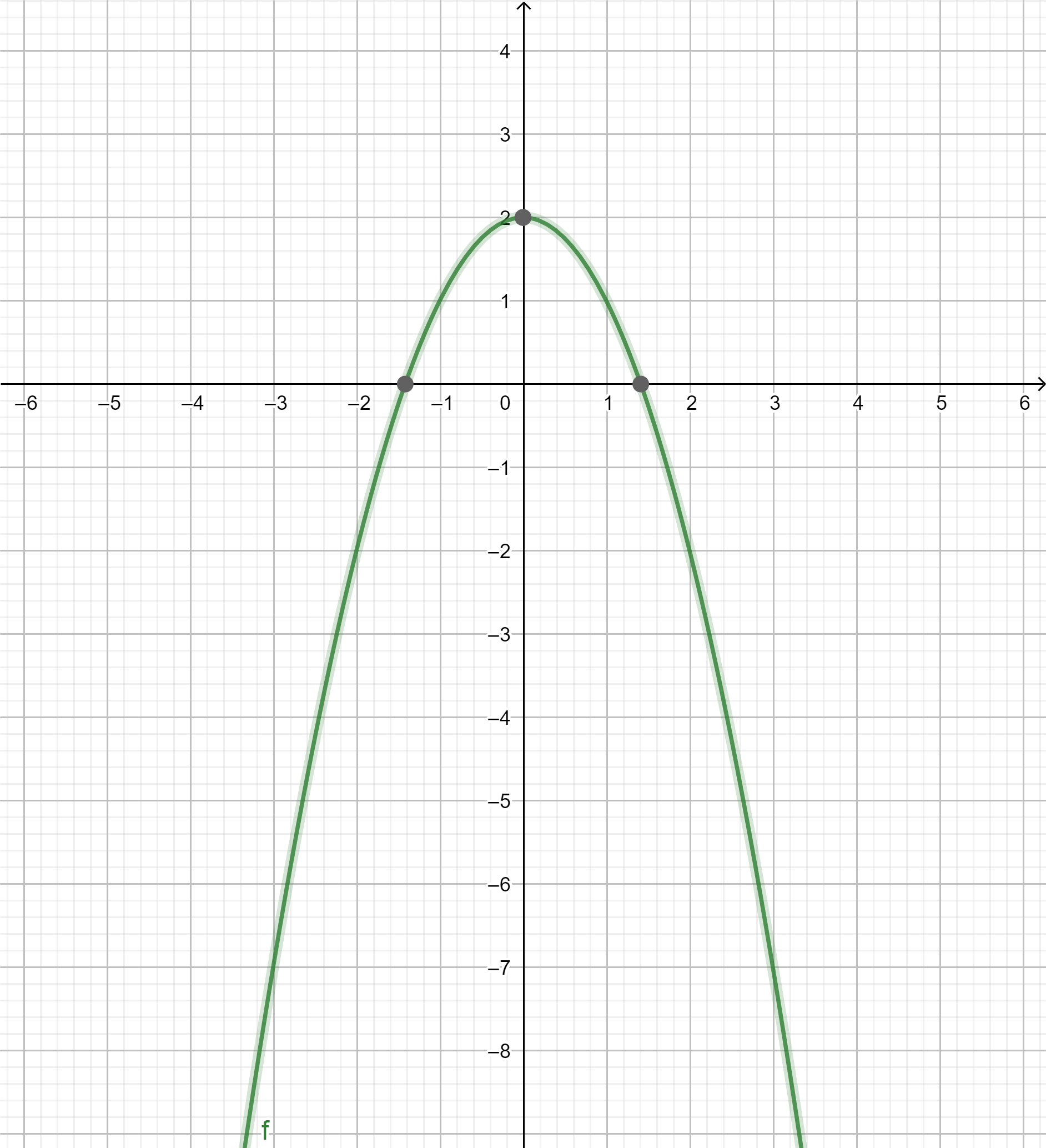
Gegeben ist die Funktion $g \mapsto \ln (2 - x^{2})$ mit maximaler Definitionsmenge $D_{g}$ .
a) Skizzieren Sie die Parabel mit der Gleichung $y = 2 - x^{2}$ in einem Koordinatensystem und geben Sie $D_{g}$ an.
b) Ermitteln Sie den Term der Ableitungsfunktion $g^{'}$ von $g$ .

Teilaufgabe a)
Der Graph der Funktion $y = x^{2}$ ist eine Normalparabel. Sie hat ihren Scheitel im Koordinatenursprung. Den Graph von $y = 2 - x^{2}$ erhält man, indem man die Normalparabel an der $x$ -Achse spiegelt und um 2 Einheiten nach oben verschiebt.
$2 - x^{2} > 0 \Leftrightarrow - \sqrt{2} < x < \sqrt{2}$
Damit ist der Definitionsbereich von $g$ :
$D_{g} =] - \sqrt{2}; \sqrt{2} [$
Teilaufgabe b)
Die Funktion $g (x) = \ln {(2 - x^{2})}_{}$ ist eine verkettete Funktion. Die $\ln$ -Funktion ist die äußere, und $y = 2 - x^{2}$ ist die innere Funktion. Mit Anwendung der Kettenregel berechnet man die 1.Ableitung.
$g^{'} (x) = \frac{1}{2 - x^{2}} \cdot (- 2 \cdot x) = - 2 \cdot \frac{x}{2 - x^{2}}$ .
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
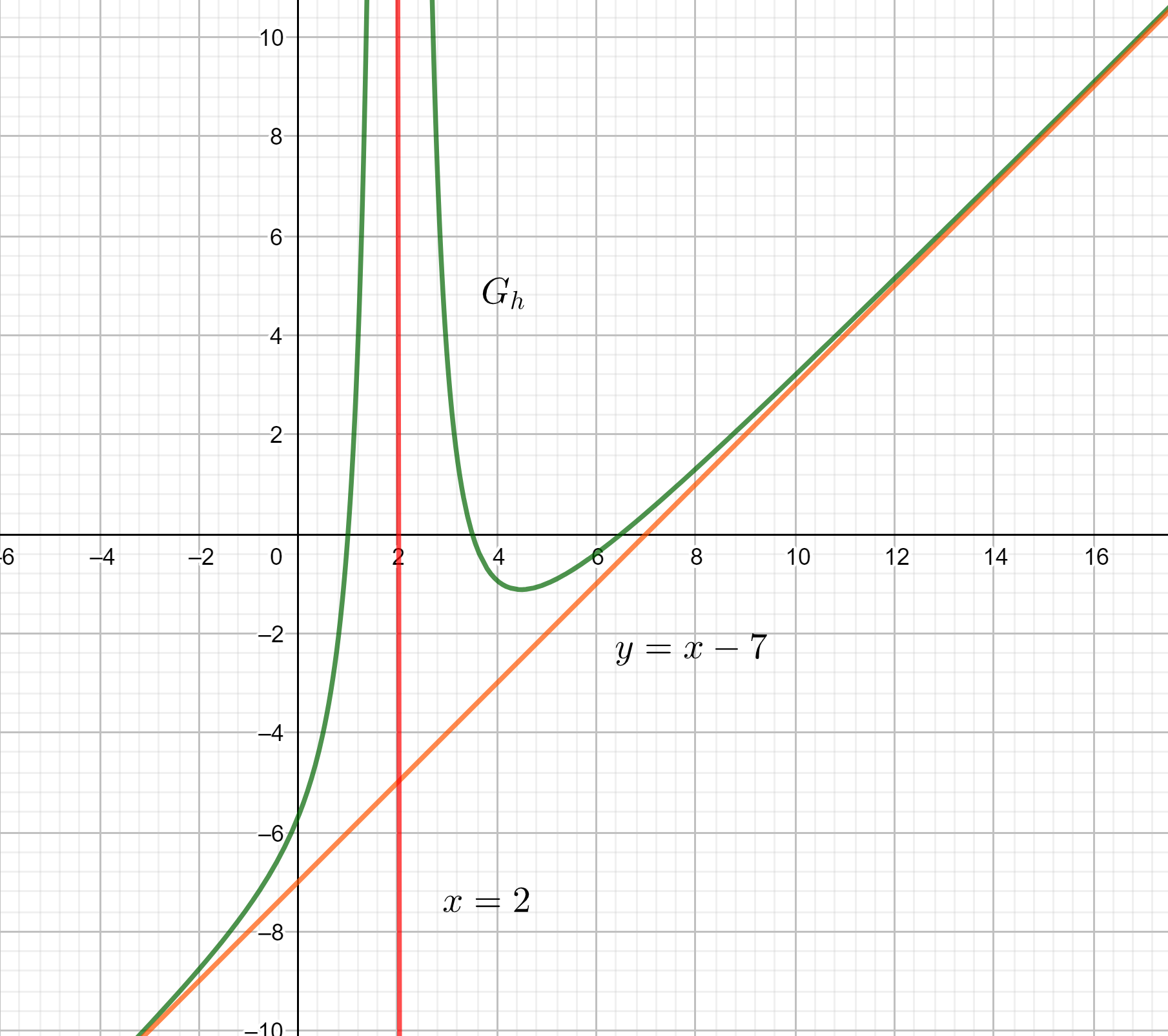
Die Abbildung 1 zeigt einen Teil des Graphen $G_{h}$ einer in $ℝ$ \ {2} definierten gebrochen-rationalen Funktion h. Die Funktion h bei x = 2 eine Polstelle ohne Vorzeichenwechsel; zudem besitzt $G_{h}$ die Gerade mit der Gleichung y = x - 7 als schräge Asymptote.
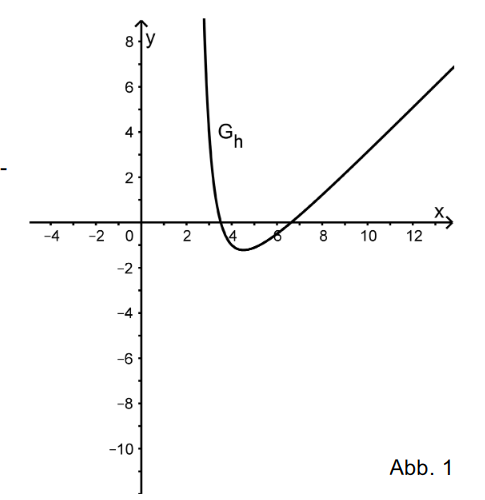
a) Zeichnen Sie in die Abbildung 1 die Asymptoten von $G_{h}$ ein und skizzieren Sie im Bereich x<2 einen möglichen Verlauf von $G_{h}$ .
b) Berechnen Sie unter Berücksichtigung des asymptotischen Verhaltens von $G_{h}$ einen Näherungswert für $\int_{10}^{20} h (x) d x$ .

a) Da $x = 2$ als doppelte Nullstelle der Nennerfunktion gewählt werden kann (es gibt ja keinen Vorzeichenwechsel) und $y = x - 7$ Asymptote ist, ergibt sich mit der senkrechten Asymptoten $x = 2$ etwa dieses Bild des Graphen:
b) Im Bereich 1 $0 \leq x \leq 20$ ist $h (x) \approx x - 7$ . Daher ist
$\int_{10}^{20} h (x) d x \approx \int_{10}^{20} (x - 7) d x = {[\frac{x^{2}}{2} - 7 x]}_{10}^{20}$
$= \frac{400}{2} - 140 - \frac{100}{2} + 70 = 200 - 140 - 50 + 70 = 80$
Wie man in der Skizze sieht, liegt der wirkliche Wert etwas darüber - die Funktion verläuft ja oberhalb ihrer Asymptote.
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Gegeben ist die in $ℝ$ definierte Funktion $k$ : $x$ $\mapsto \frac{- x^{2} + 2 x}{2 x^{2} + 4}$ . Ihr Graph wird mit $G_{k}$ bezeichnet.
a) Geben Sie die Nullstellen von $k$ an und begründen Sie anhand des Funktionsterms, dass $G_{k}$ die Gerade mit der Gleichung $y = - 0,5$ als waagrechte Asymptote besitzt.
b) Berechnen Sie die $x$ -Koordinate des Schnittpunkts von $G_{k}$ mit der waagrechten Asymptote.

Teilaufgabe a)
Eine gebrochen rationale Funktion hat dort eine Nullstelle wo der Zähler Null wird.
Bei der vorgelegten Funktion ist der Nenner für alle reellen $x$ positiv. Somit ist $k$ für alle reellen $x$ definiert.
$k (x) = 0 \Leftrightarrow - x^{2} + 2 \cdot x$ =0
$x \cdot (- x + 2) = 0 \Leftrightarrow x = 0 oder x = 2$
Die vorgelegte Funktion $k$ ist eine gebrochen rationale Funktion, wobei Zählergrad gleich Nennergrad ist. Somit ist die zur $x$ -Achse parallele Gerade $y = - \frac{1}{2}$ Asymptote.
Zur Begründung: Dividiert man Zähler und Nenner durch die höchste Potenz von $x$ und erhält:
$k (x) = \frac{- x^{2} + 2 x}{2 x^{2} + 4} = \frac{- 1 + \frac{2}{x}}{2 + \frac{4}{x^{2}}}$ . Betrachtet man nun den Funktionsterm für unbegrenzt wachsendes bzw. fallendes $x$ , so streben die Bruchterme $\frac{2}{x} und \frac{4}{x^{2}}$ gegen Null und die Funktion $k$ strebt gegen $- \frac{1}{2}$ .
Teilaufgabe b)
$- \frac{1}{2} = \frac{- x^{2} + 2 x}{2 x^{2} + 4} \Leftrightarrow - 2 x^{2} - 4 = - 2 x^{2} + 4 x \Leftrightarrow - 4 = 4 \cdot x \Leftrightarrow x = - 1$
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Abbildung 2 zeigt den Graphen $G_{f}$ einer in [0,8; + ∞ [ definierten Funktion $f$ .
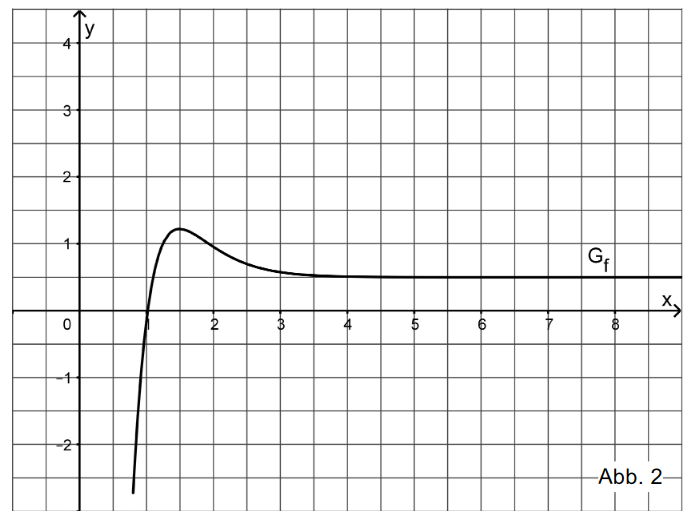
Betrachtet wird zudem die in [0,8; + ∞ [ definierte Integralfunktion J:
$x \mapsto \int_{2}^{x} f (t) d t .$
Begründen Sie mithilfe von Abbildung 2, dass J(1) ≈ -1 gilt, und geben Sie einen Näherungswert für den Funktionswert J(4,5) an. Skizzieren Sie den Graphen von J in der Abbildung.

$J (1) = \int_{2}^{1} f (x) d x = - \int_{1}^{2} f (x) d x .$
Aus der Abbildung Abb2. kann man an der Anzahl der Quadrate ablesen, dass $\int_{1}^{2} f (x) d x = 1$ (etwa) gilt.
Also $J (1) = - 1.$
Ebenfalls durch Abzählen der eingeschlossenen Quadrate erhalten wir für $J (4,5) = \int_{2}^{4,5} f (x) d x = 1,5$ (etwa).
Ein Quadrat hat einen Flächeninhalt von $\frac{1}{4} F E$ (Flächeneinheit ).
Lösung als Video mit Erklärung des Graphen