Aufgaben zur Stetigkeit anhand von Graphen
Hier findest du Übungsaufgaben zum Thema Stetigkeit. Lerne, Stetigkeit anhand eines Funktionsgraphen zu erkennen!
- 1
Welche der Funktionen ist im dargestellten Bereich stetig?
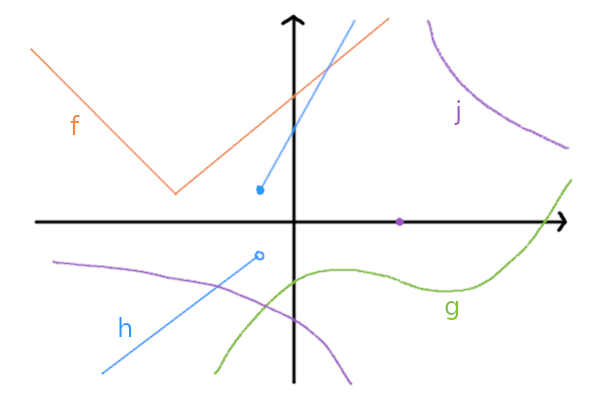
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
