Die folgende Abbildung zeigt den Querschnitt eines Springbrunnens. Dieser hat eine kreisförmige Grundfläche mit einem Durchmesser von 4 m. Die Oberflächenlinie der im Querschnitt dargestellten Auffangwanne wird durch den Graphen einer ganzrationalen Funktion g vierten Grades mit der Definitionsmenge beschrieben. Der Graph in einem kartesischen Koordinatensystem ist achsensymmetrisch zur y-Achse. Die Koordinaten x und y stellen Längenangaben in der Einheit Meter dar. Bei den folgenden Rechnungen kann auf das Mitführen von Einheiten verzichtet werden.
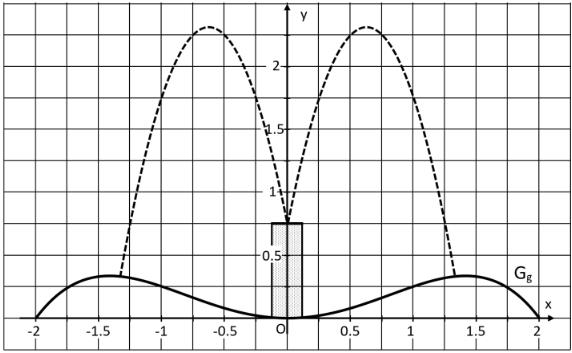
Bestimmen Sie die Funktionsgleichung von g. Entnehmen Sie dazu geeignete Werte aus der Zeichnung.
[Mögliches Ergebnis: ]
Die Wasserfontänen treten – wie in obiger Abbildung gestrichelt dargestellt – aus einer in der Mitte befindlichen Säule aus und beschreiben Parabelbahnen. Ihr Verlauf ist abhängig vom Wasserdruck. Im Folgenden wird nur die rechte Wasserfontäne betrachtet. Alle möglichen Wasserstrahlen lassen sich durch die Graphen der Funktionen
und darstellen.
1.) Berechnen Sie, für welchen Wert von a der Strahl im Punkt A auf die Auffangwanne trifft.
2.) Berechnen Sie, bis zu welcher maximalen Höhe die Auffangwanne gefüllt werden kann, bevor sie überläuft.
