Teil 2 Analysis I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
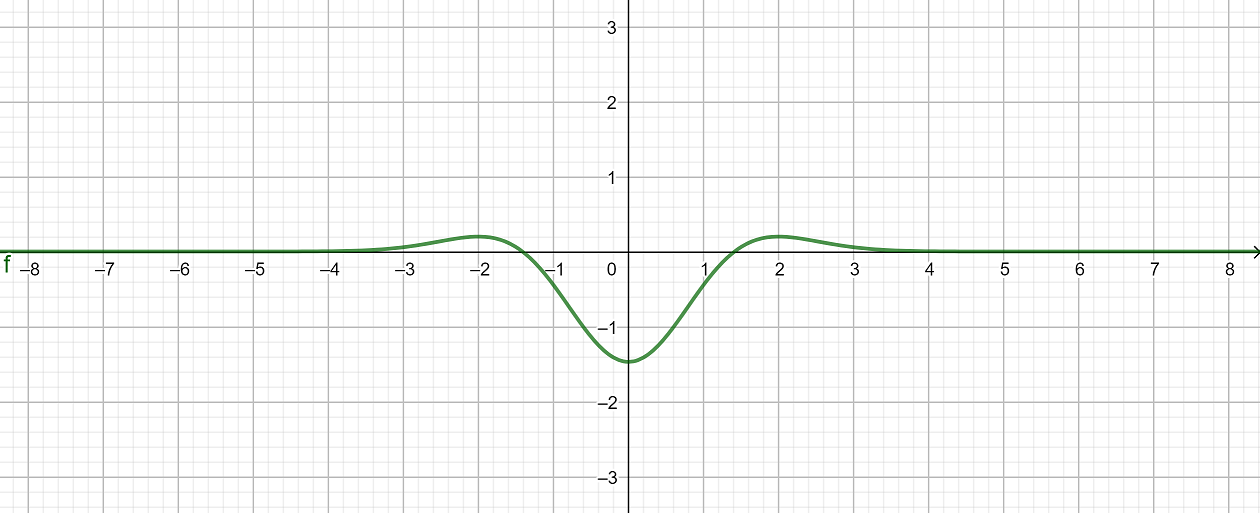
Gegeben ist die Funktion $f:x \rightarrow (2x^2-4)\cdot e^{- \dfrac{1}{2}x^2-1}$ mit der Definitionsmenge $D_f= \mathbb{R}$ . Der Graph von f in einem kartesischen Koordinatensystem wird mit $G_f$ bezeichnet.
1. Untersuchen Sie das Symmetrieverhalten des Graphen $G_f$ bezüglich des Koordinatensystems sowie das Verhalten der Funktionswerte von $f$ für $|x| \rightarrow \infty$ .
2. Ermitteln Sie jeweils die Art und die Koordinaten der relativen Extrempunkte von $G_f$ und geben Sie die Wertemenge $W_f$ der Funktion f an.
  [Teilergebnis: $f'(x)=(8x-2x^3)\cdot e^{-\frac{1}{2}x^{^2}-1}$ ]
3. Stellen Sie die Gleichung der Tangente an $G_f$ an der Stelle $x=1$ in allgemeiner Form auf.
4. Bestimmen Sie die Nullstellen der Funktion f und zeichnen Sie unter Verwendung aller bisherigen Ergebnisse und weiterer geeigneter Funktionswerte den Graphen von f für $-3\leq x \leq 3$ in ein kartesisches Koordinatensystem.
  Maßstab für beide Achsen: 1 LE = 2 cm
5. Der Graph der Ableitungsfunktion von f und die x-Achse schließen im I. Quadranten des kartesischen Koordinatensystems im Bereich $0 \leq x \leq 2$ ein endliches Flächenstück ein. Berechnen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks auf zwei Nachkommastellen gerundet.
6. Der Graph $G_f$ und die Koordinatenachsen schließen im IV. Quadranten ein endliches Flächenstück ein. Schätzen Sie die Maßzahl des Flächeninhalts dieses Flächenstücks geeignet ab.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die folgende Abbildung zeigt den Querschnitt eines Springbrunnens. Dieser hat eine kreisförmige Grundfläche mit einem Durchmesser von 4 m. Die Oberflächenlinie der im Querschnitt dargestellten Auffangwanne wird durch den Graphen $G_g$ einer ganzrationalen Funktion g vierten Grades mit der Definitionsmenge $D_g=[-2{,}2]$ beschrieben. Der Graph $G_g$ in einem kartesischen Koordinatensystem ist achsensymmetrisch zur y-Achse. Die Koordinaten x und y stellen Längenangaben in der Einheit Meter dar. Bei den folgenden Rechnungen kann auf das Mitführen von Einheiten verzichtet werden.
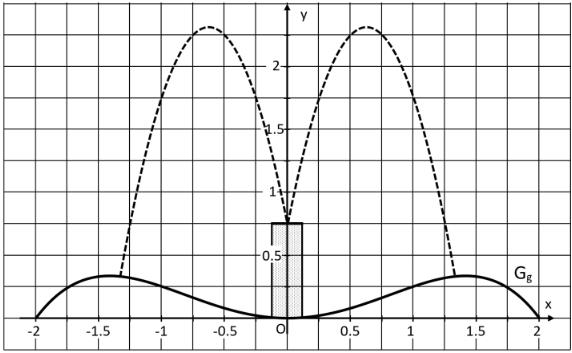
1. Bestimmen Sie die Funktionsgleichung von g. Entnehmen Sie dazu geeignete Werte aus der Zeichnung.
  [Mögliches Ergebnis: $g(x)=-\dfrac{1}{12}x^4+\dfrac{1}{3}x^2$ ]
2. Die Wasserfontänen treten – wie in obiger Abbildung gestrichelt dargestellt – aus einer in der Mitte befindlichen Säule aus und beschreiben Parabelbahnen. Ihr Verlauf ist abhängig vom Wasserdruck. Im Folgenden wird nur die rechte Wasserfontäne betrachtet. Alle möglichen Wasserstrahlen lassen sich durch die Graphen der Funktionen
  $p_a(x)=-ax^2+5x+0{,}75$ und $a \in\mathbb{R}^+$ darstellen.
  1.) Berechnen Sie, für welchen Wert von a der Strahl im Punkt A $(1|0{,}25)$ auf die Auffangwanne trifft.
  2.) Berechnen Sie, bis zu welcher maximalen Höhe $h_{max}$ die Auffangwanne gefüllt werden kann, bevor sie überläuft.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?