1 Addition und Subtraktion: gleichnamige Brüche
Tom bekommt heute sein Lieblingsessen, Pizza! Er zerteilt die Pizza in gleich große Stücke. Ein Stück ist der zwölfte Teil der gesamten Pizza, d. h. . Tom isst Stücke, d. h. , sein Freund Stücke, das heißt .
Welchen Bruchteil der Pizza essen die beiden zusammen?
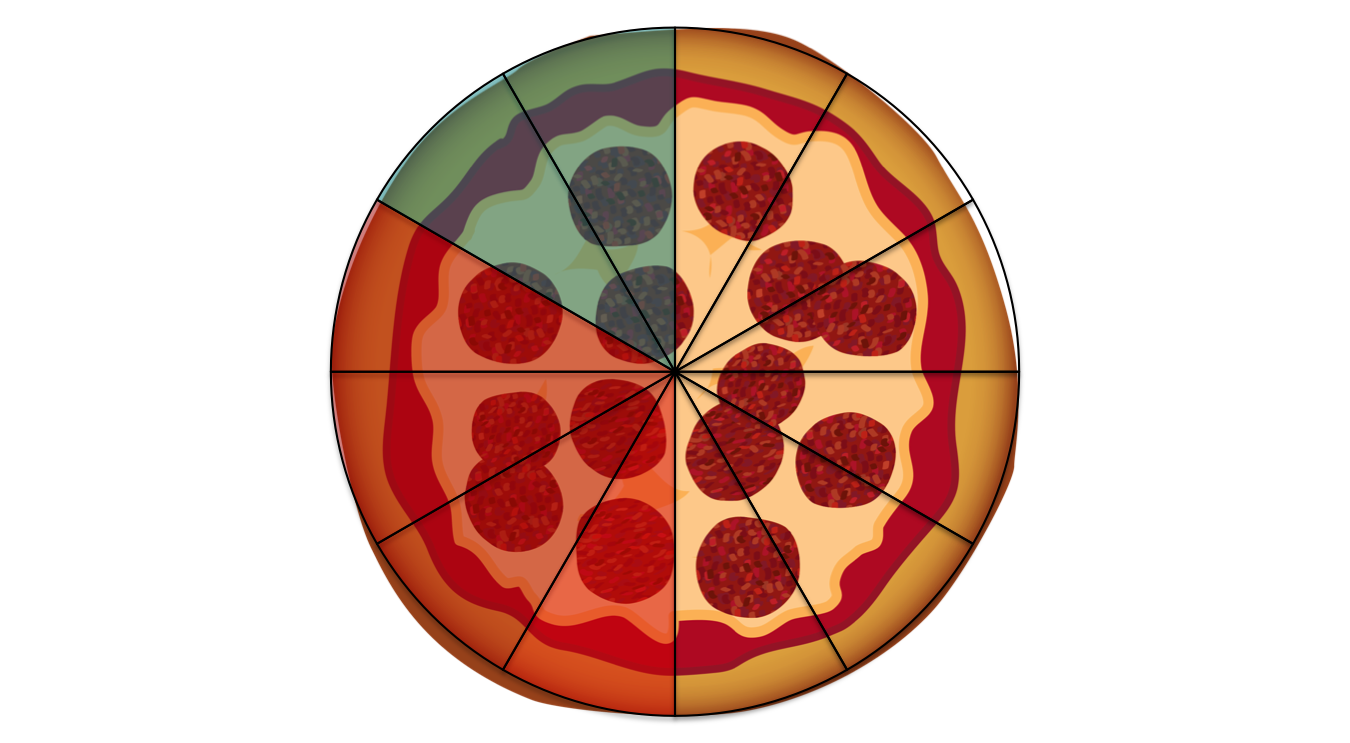
Die beiden haben zusammen Stücke gegessen, also den Bruchteil . Dahinter steht die Rechnung
Wir sehen also, dass bei der Addition gleichnamiger Brüche die Zähler addiert werden, während der Nenner gleich bleibt.
Welcher Bruchteil der Pizza bleibt übrig?
Wie auch in der Grafik zu sehen, bleiben Stücke übrig, also der Bruchteil . Dahinter steht die Rechnung
Wir sehen also, dass bei der Subtraktion gleichnamiger Brüche die Zähler subtrahiert werden, während der Nenner gleich bleibt.
Addition gleichnamiger Brüche:
Die Zähler der Brüche werden addiert, der Nenner beibehalten:
Subtraktion gleichnamiger Brüche:
Die Zähler der Brüche werden subtrahiert, der Nenner beibehalten:
Das Ergebnis kann oft noch gekürzt werden.
Übungsaufgaben
Berechne die folgenden Terme und kürze das Ergebnis vollständig
2 Addition und Subtraktion: ungleichnamige Brüche
Wir haben im vorherigen Abschnitt gesehen, wie man gleichnamige Brüche addiert und subtrahiert. Wir wollen uns nun anschauen, wie man mit Brüchen rechnet, die unterschiedliche Nenner besitzen, z. B. und .
Dazu bietet es sich an, die Brüche durch Rechtecke zu veranschaulichen:


Die Addition kann man veranschaulichen, indem man die beiden Rechtecke übereinander legt.
Man kann sehen, dass sich eine neue Zerteilung des Rechtecks bildet, und zwar in Teile. Es sind Teile türkis und Teile rot gefärbt. Zusammen also Teile. Hierbei muss man in der grafischen Veranschaulichung beachten, dass die oberen beiden linken Teile doppelt gezählt werden müssen, da sie in beiden Rechtecken gefärbt werden.

Mathematisch passiert Folgendes: Die neue Zerteilung entspricht Erweitern auf denselben Hauptnenner:
Anschließend kann man diese beiden Brüche so addieren, wie wir es im vorherigen Abschnitt gelernt haben, d. h. die Zähler werden addiert und der Nenner bleibt gleich:
Wir sehen also, dass wir die Addition ungleichnamiger Brüche dadurch berechnen können, indem wir vorher die Brüche auf denselben Hauptnenner erweitern. Dasselbe Verfahren können wir auch bei der Subtraktion verwenden.
Finde einen gemeinsamen Nenner (Hauptnenner)
Erweitere die Brüche auf den gemeinsamen Nenner
Addiere bzw. subtrahiere die Zähler
Kürze das Ergebnis vollständig
Übungsaufgaben
Berechne die folgenden Terme und kürze das Ergebnis vollständig
3 Übungsaufgaben
Laden
Weitere Aufgaben findest du hier: Aufgaben zur Addition und Subtraktion von Brüchen
4 Multiplikation: natürliche Zahl mal Bruch
Schauen wir uns nochmal unser Pizza-Beispiel von vorher an: Tom hat Stücke, d. h. den Bruchteil gegessen, sein Freund Stücke, d. h. . Sein Freund isst also doppelt so viele Stücke wie Tom. Dahinter steht die Rechnung

Von den natürlichen und ganzen Zahlen kennst du bereits, dass gilt: . Die Multiplikation ist also eine wiederholte Addition.
Genauso gilt das bei der Multiplikation von natürlichen Zahlen mit Brüchen.
Wir sehen also:
Multiplizieren wir eine natürlichen Zahl mit einem Bruch, so wird der Zähler mit dieser Zahl multipliziert, während der Nenner gleich bleibt.
Übungsaufgaben
5 Multiplikation: Bruch mal natürliche Zahl
Nach so viel Pizza haben Tom und sein Freund Durst. Im Supermarkt ist eine Liter Flasche Cola im Angebot. Sie schaffen aber nur der Flasche auszutrinken.
Wie viele Liter Cola haben die beiden getrunken?

Wir müssen als von berechnen. Anschaulich können wir uns das so vorstellen:
Jeder Balken entspricht Liter, von dem jeweils ausgetrunken wurden. Insgesamt wurden also ausgetrunken. Es gilt also:
von =
Rechnen können wir das so:
von =
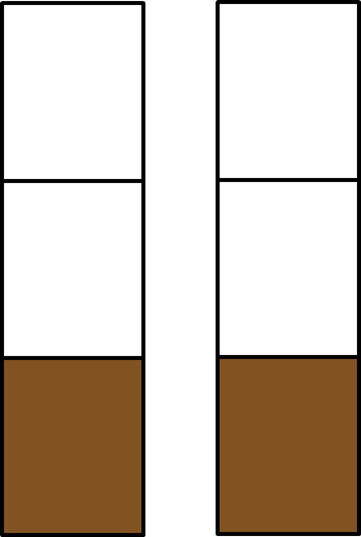
Wir sehen also:
Multiplizieren wir einen Bruch mit einer natürlichen Zahl, so wird der Zähler mit dieser Zahl multipliziert, während der Nenner gleich bleibt.
Übungsaufgaben
6 Multiplikation: Bruch mal Bruch
Tom hat eine Packung Bonbons dabei, die noch voll ist. Davon isst Tom auf.
Wie viel von der ursprünglichen Packung hat Tom gegessen?

Wir wollen also wissen, wie viel von ist.
Zunächst veranschaulichen wir uns , indem wir ein Rechteck, das die Packung darstellen soll, in 4 gleich große Teile teilen. Du kannst dasselbe auch mit einem Blatt Papier nachfalten.

Als Nächstes veranschaulichen wir uns auf dieselbe Art und Weise, indem wir das Rechteck (Papier) längs in gleich große Teile teilen (falten).
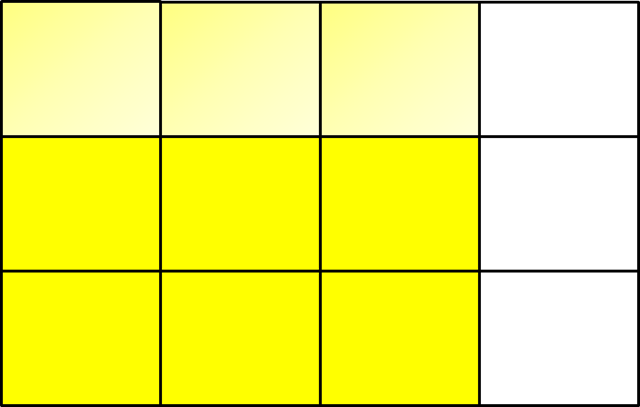
Wenn wir nun von markieren, können wir abzählen, dass der ursprünglichen Tüte markiert sind. Also gilt: von
Rechnen können wir das so:
von
Wir sehen also:
Oft können wir das Ergebnis noch kürzen. In unserem Beispiel können wir Zähler und Nenner noch mit 3 kürzen und erhalten:
Übungsaufgaben
7 Übungsaufgaben
8 Division: Bruch geteilt durch ganze Zahl
Im vorigen Abschnitt haben wir berechnet, dass Tom und sein Freund zusammen Liter Cola getrunken haben. Rechts siehst du die getrunkene Cola veranschaulicht.
Wenn beide genau gleich viel getrunken haben, wie viel Liter Cola hat dann Tom getrunken?
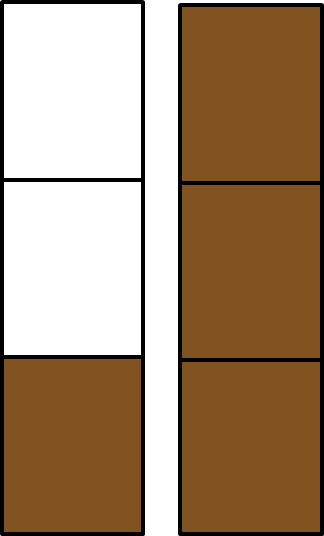
Wir müssen also geteilt durch berechnen. Anschaulich können wir uns das so vorstellen, dass wir jeden der Teile halbieren.
Dann können wir ablesen, dass Tom Liter getrunken hat. Es gilt also .
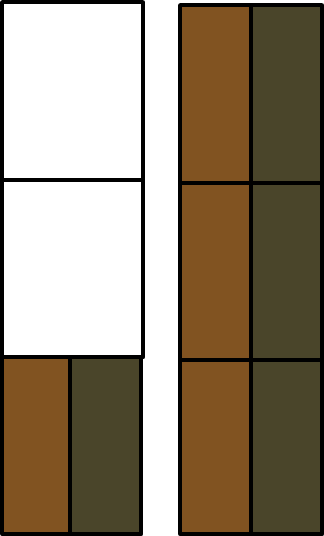
Weiteres Beispiel
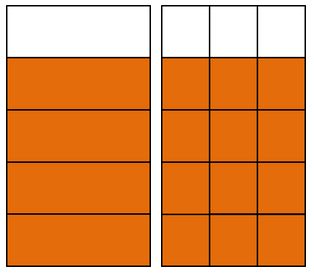
Anna, Lisa und Marie teilen sich Liter Apfelschorle.
Wie viel Saft bekommt Anna?

Wir teilen jedes der Teile in gleiche Teile und können dann ablesen:
Anna bekommt also Liter Apfelsaft.
Überlegungen zur Rechenregel
Schauen wir uns die Rechnungen der zwei Beispiele nochmal genauer an:
und
Im ersten Beispiel bedeutet das , dass wir "die Hälfte" von nehmen. Wir können also auch schreiben.
Genauso bedeutet im zweiten Beispiel , dass wir den "dritten Teil" von nehmen. Wir können also auch schreiben.
Wir können also anstatt durch eine ganze Zahl zu dividieren, auch mit dem Kehrbruch multiplizieren. Dabei ist der Kehrbruch von und der Kehrbruch von .
Übungsaufgaben
Der Kehrwert von ist…
Der Kehrwert von ist…
Der Kehrwert von ist…
Merke:
Wir dividieren einen Bruch durch eine ganze Zahl, indem wir den Bruch mit dem Kehrbruch multiplizieren.
Übungsaufgaben
9 Division: Bruch geteilt durch Bruch
Tom und sein Freund haben noch Liter Cola übrig. Sie wollen sie in kleinere, handlichere Flaschen umfüllen. In jeder kleinen Flasche ist Platz für Liter. Wie viele Flaschen brauchen sie?
Zunächst schauen wir uns ein einfacheres Beispiel an. Wenn wir Liter in Liter-Flaschen abfüllen wollen, rechnen wir: . Man braucht also Flaschen, um Liter in Liter-Flaschen abzufüllen.
Genauso können wir nun berechnen, wie viele Flaschen Tom und sein Freund brauchen. Wir rechnen:
Versuchen wir uns diese Rechnung wieder bildlich zu veranschaulichen. Links siehst du die Liter. Rechts die gleiche Menge Cola, allerdings in Liter Unterteilungen. Daran können wir erkennen, dass Tom und sein Freund insgesamt kleine Flaschen brauchen. Die dritte Flasche ist allerdings nur zu gefüllt.
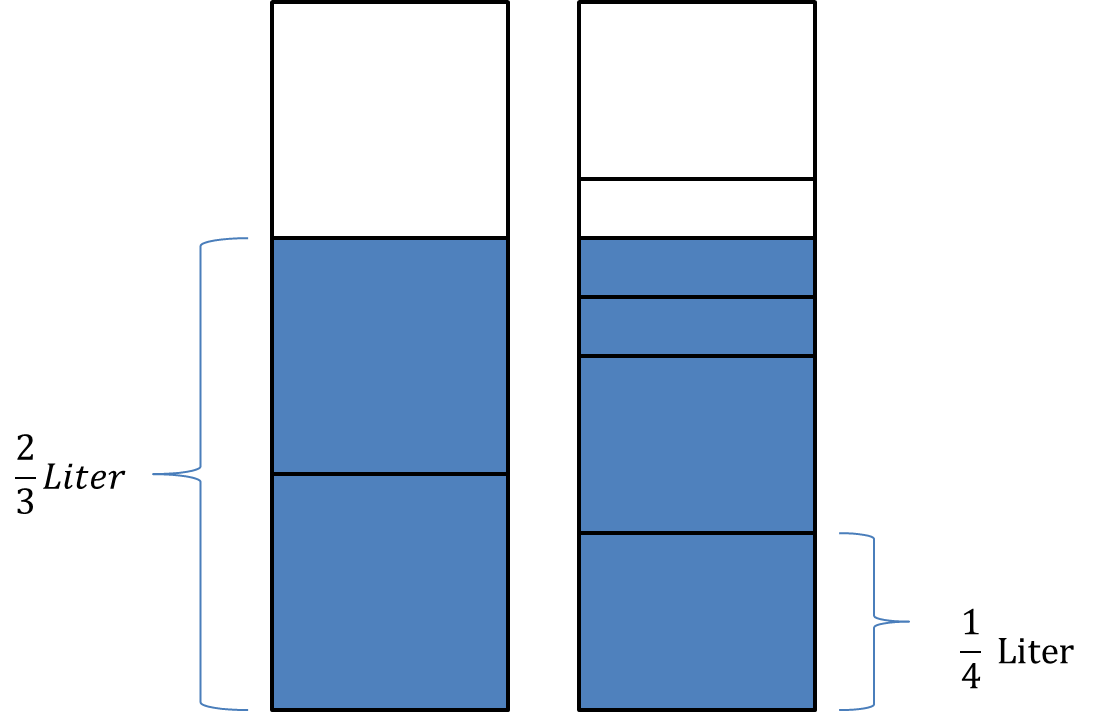
Insgesamt gilt:
Im letzten Schritt haben wir den gemischten Bruch umgewandelt.
Im vorigen Kapitel hast du gelernt, dass wir anstatt durch eine Zahl zu dividieren auch mit dem Kehrbruch multiplizieren können. Das Gleiche gilt auch bei der Division durch einen Bruch.
Wir erhalten den Kehrbruch eines Bruchs, indem wir Zähler und Nenner vertauschen. So ist der Kehrbruch von gleich und es gilt .
Wir können also rechnen:
Merke:
