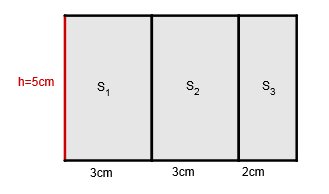
Berechne Volumen und Oberfläche, wenn der Körper jeweils die Höhe hat:
Prisma mit gleichschenkligem Dreieck als Grundfläche, Schenkellänge und Basis .
Zylinder mit Radius
Gerade Pyramide (alle Seitenkanten gleich lang) mit Quadrat der Kantenlänge als Grundfläche.
Kegel mit Radius
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl → Was bedeutet das?