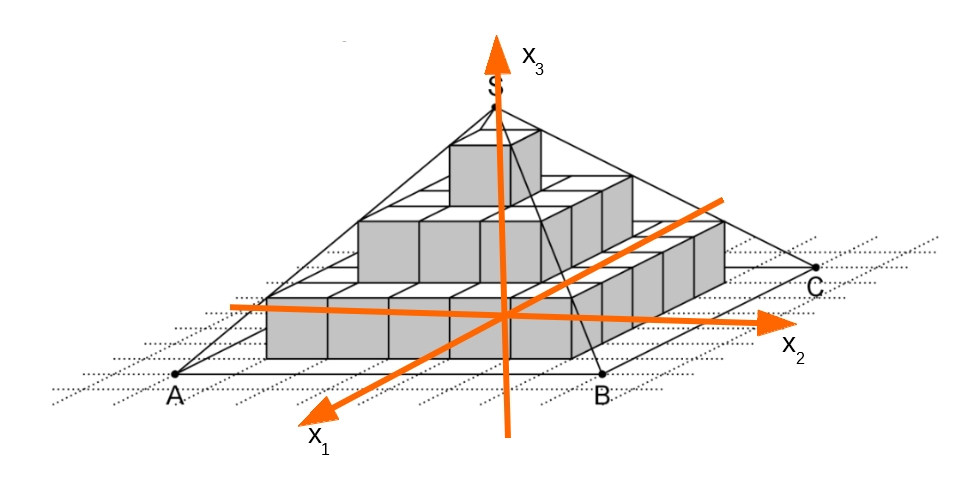
Die Abbildung zeigt die Pyramide mit quadratischer Grundfläche . Der Pyramide ist eine Stufenpyramide einbeschrieben, die aus Würfeln mit der Kantenlänge 1 besteht.
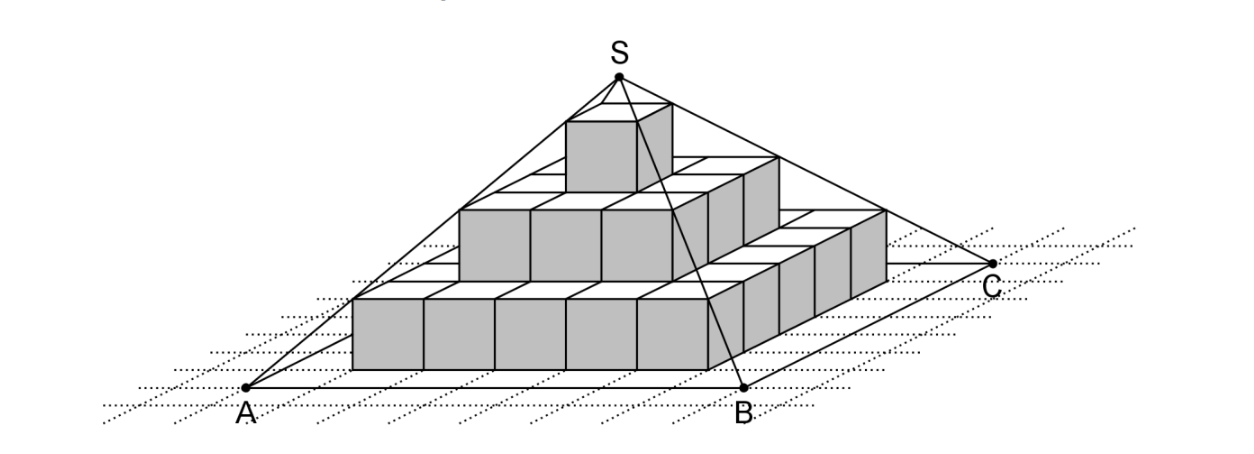
Geben Sie das Volumen der Stufenpyramide und die Höhe der Pyramide an. (2 BE)
Bestimmen Sie unter Verwendung eines geeignet gewählten kartesischen Koordinatensystems eine Gleichung für die Gerade, die durch die Punkte und verläuft. Zeichnen Sie das gewählte Koordinatensystem in die Abbildung ein. (3 BE)