Geometrie, Teil A, Aufgabengruppe 2

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
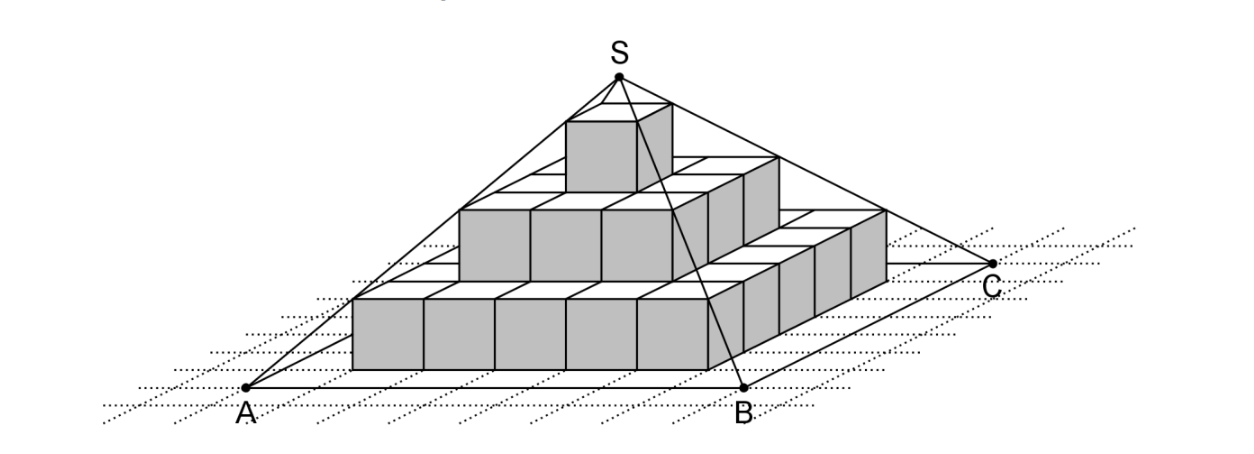
Die Abbildung zeigt die Pyramide $A B C D S$ mit quadratischer Grundfläche $A B C D$ . Der Pyramide ist eine Stufenpyramide einbeschrieben, die aus Würfeln mit der Kantenlänge 1 besteht.
1. Geben Sie das Volumen der Stufenpyramide und die Höhe der Pyramide $A B C D S$ an. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satzes von Pythagoras
  Hier solltest du Seiten in rechtwinkligen Dreiecken ausrechnen können, am einfachsten mit Hilfe des Satzes von Pythagoras.
  Volumen der Stufenpyramide
  Jede der Würfelflächen ist quadratisch, das heißt die unterste Fläche besteht aus $5\cdot 5=25$ , die mittlere aus $3\cdot 3=9$ und die oberste aus $1\cdot 1=1$ Würfel. Insgesamt sind es also $25 + 9 + 1 = 35$ Würfel.
  Jeder Würfel hat den Flächeninhalt $1\cdot1\cdot1=1$ VE.
  Also hat die Pyramide $35\cdot 1=35$ VE.
  Höhe der Pyramide $A B C D S$
  Die Höhe der Pyramide besteht aus drei Klötzen, also $3$ LE und dem kleinen Stück vom obersten Klotz bis zu $S$ . Dieses kleine Stück hat genau die Höhe eines halben Klotzes, weil die Kante der Pyramide gleichmäßig ansteigt und $S$ genau in der Mitte der Pyramide ist. Insgesamt beträgt die Höhe damit $3 + 0,5 = 3,5$ LE.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
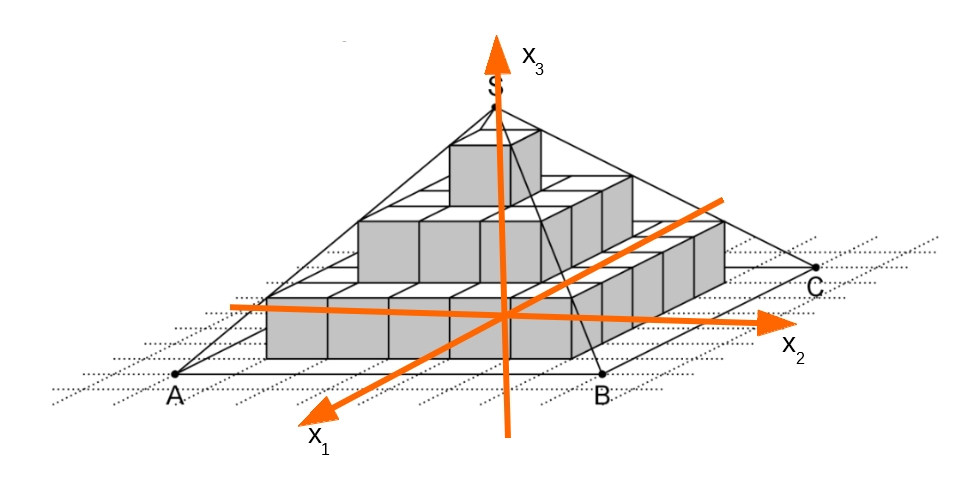
2. Bestimmen Sie unter Verwendung eines geeignet gewählten kartesischen Koordinatensystems eine Gleichung für die Gerade, die durch die Punkte $B$ und $S$ verläuft. Zeichnen Sie das gewählte Koordinatensystem in die Abbildung ein. (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Koordinatensystem
  Es gibt mehrere Positionen, die sich für ein Koordinatensystem eignen. Am besten ist es, wenn einer oder sogar beide Punkte dadurch einfache Koordinaten haben. Achte darauf, die drei Achsen zu beschriften. Ein Beispiel siehst du hier:
  Aufstellen der Gerade
  Mit diesem Koordinatensystem hat $S$ die Koordinaten $(0 ∣ 0 ∣ 3,5)$ (die 3. Koordinate entspricht der in Teil a) bestimmten Höhe) und $B$ die Koordinaten $(3,5 ∣ 3,5 ∣ 0)$ , was man durch abzählen der Kästchen rausfinden kann.
  Eine Gerade hat grundsätzlich die Form:
  $g \colon \quad \vec x = \vec p + \lambda \vec u$
  Setze die entsprechenden Punkte dieser Aufgabe ein (es gibt nicht nur eine richtige Lösung!).
  $g \colon \quad\vec x= \overrightarrow{OS} + \lambda \overrightarrow{SB}$
  Berechne $\overrightarrow{SB}$
  $\overrightarrow{SB}=\overrightarrow{OB}-\overrightarrow{OS}=\begin{pmatrix}3{,}5\\3{,}5\\0\end{pmatrix}-\begin{pmatrix}0\\0\\3{,}5\end{pmatrix}=\begin{pmatrix}3{,}5\\3{,}5\\-3{,}5\end{pmatrix}$
  Setze in die allgemeine Geradengleichung ein.
  $g \colon \quad\vec x= \begin{pmatrix}0\\0\\-3{,}5\end{pmatrix} + \lambda \begin{pmatrix}3{,}5\\3{,}5\\-3{,}5\end{pmatrix}$
  Beachte, dass diese Lösung nicht eindeutig ist. Jeder andere Geradenpunkt (insbesondere $B$ ) eignet sich genauso als Aufpunkt und alle Vielfachen des Richtungsvektors sind genauso richtig.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Gerade $g$ verläuft durch die Punkte $A (0 ∣ 1 ∣ 2)$ und $B (2 ∣ 5 ∣ 6)$ .
1. Zeigen Sie, dass die Punkte $A$ und $B$ den Abstand $6$ haben. Die Punkte $C$ und $D$ liegen auf $g$ und haben von $A$ jeweils den Abstand $12$ .
  Bestimmen Sie die Koordinaten von $C$ und $D$ . (3 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Abstand zwischen zwei Punkten
  Für diese Aufgabe musst du wissen, wie du den Abstand zwischen zwei Punkten ausrechnest. Außerdem musst du Vektoren addieren und multiplizieren können.
  Abstand der Punkte $A$ und $B$
  Dafür berechnest du den Betrag des Verbindungsvektors zwischen $A$ und $B$ :
  $\overrightarrow{AB} = \overrightarrow{B} - \overrightarrow{A} =\begin{pmatrix}2\\5\\6\end{pmatrix} - \begin{pmatrix}0\\1\\2\end{pmatrix}=\begin{pmatrix}2\\4\\4\end{pmatrix}$
  $\left|\,\overrightarrow{AB} \,\right|=\left|\begin{pmatrix}2\\4\\4\end{pmatrix}\right|\displaystyle=\sqrt{2^2+4^2+4^2}=\sqrt{36}=6$
  Die Punkte $A$ und $B$ haben den Abstand $6$ Längeneinheiten voneinander, wie man zeigen sollte. Statt dem Vektor $\overrightarrow{AB}$ kann man natürlich genauso den Vektor $\overrightarrow{BA}$ verwenden.
  Koordinaten von $B$ und $C$
  $\overrightarrow{AB}$ ist ein Richtungsvektor der Geraden mit der Länge $6$ . Sucht man jetzt Punkte, die auf der Geraden liegen und den Abstand $12$ von $A$ haben, muss man zum Punkt $A$ gehörigen Vektor nur zweimal den Vektor $\overrightarrow{AB}$ addieren bzw. subtrahieren:
  $\overrightarrow{0C}=\overrightarrow{0A}+2\cdot \overrightarrow{AB}=\begin{pmatrix}0\\1\\2\end{pmatrix} +2\cdot \begin{pmatrix}2\\4\\4\end{pmatrix}=\begin{pmatrix}0\\1\\2\end{pmatrix} +\begin{pmatrix}4\\8\\8\end{pmatrix}=\begin{pmatrix}4\\9\\10\end{pmatrix}$
  und
  $\overrightarrow{0D}=\overrightarrow{0A}-2\cdot \overrightarrow{AB}=\begin{pmatrix}0\\1\\2\end{pmatrix} -2\cdot \begin{pmatrix}2\\4\\4\end{pmatrix}=\begin{pmatrix}0\\1\\2\end{pmatrix} -\begin{pmatrix}4\\8\\8\end{pmatrix}=\begin{pmatrix}-4\\-7\\-6\end{pmatrix}$
  Damit hat der Punkt $C$ die Koordinaten $(4 ∣ 9 ∣ 10)$ und der Punkt $D$ die Koordinaten $(- 4 ∣ - 7 ∣ - 6)$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Die Punkte $A, B$ und $E (1 ∣ 2 ∣ 5)$ sollen mit einem weiteren Punkt die Eckpunkte eines Parallelogramms bilden. Für die Lage des vierten Eckpunkts gibt es mehrere Möglichkeiten. Geben Sie für zwei dieser Möglichkeiten die Koordinaten des vierten Eckpunkts an. (2 BE)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Parallelograms
  Für diese Aufgabe solltest du die Eigenschaften eines Parallelogramms kennen.
  Grundsätzlich sind drei Möglichkeiten vorstellbar, die drei vorhandenen Punkte zu einem Parallelogramm zu ergänzen. Sie sind alle in der Grafik rechts grundsätzlich dargestellt.
  Das Vorgehen zum Ermitteln eines neuen Punktes funktioniert immer gleich: Man stellt einen Verbindungsvektor zwischen zwei Punkten auf und addiert diesen zum dritten Punkt.
  Nachdem du den Vektor $\overrightarrow{AB}$ bereits kennst, lassen sich die Punkte $P_{1}$ und $P_{2}$ schneller ausrechnen:
  $\overrightarrow{OP_1}=\overrightarrow{OE}+ \overrightarrow{AB}=\begin{pmatrix}1\\2\\5\end{pmatrix} +\begin{pmatrix}2\\4\\4\end{pmatrix}=\begin{pmatrix}3\\6\\9\end{pmatrix}$
  $\overrightarrow{OP_2}=\overrightarrow{OE}- \overrightarrow{AB}=\begin{pmatrix}1\\2\\5\end{pmatrix} -\begin{pmatrix}2\\4\\4\end{pmatrix}=\begin{pmatrix}-1\\-2\\1\end{pmatrix}$
  Einen Verbindungsvektor berechnet man, indem man "Spitze minus Fuß" rechnet:
  $\overrightarrow{OP_3}=\overrightarrow{OA}+ \overrightarrow{EB}=\overrightarrow{OA}+\left[\overrightarrow{OB}-\overrightarrow{OE}\right]=\begin{pmatrix}0\\1\\2\end{pmatrix}+ \begin{pmatrix}2\\5\\6\end{pmatrix}-\begin{pmatrix}1\\2\\5\end{pmatrix}=\begin{pmatrix}1\\4\\3\end{pmatrix}$
  Die drei möglichen Punkte sind:
  $P1(3∣6∣9), \sf P_2(-1|-2|1) und \sf P_3(1|4|3)$
  Achtung: Man kann jeden der Punkte auf viele verschiedene Arten erhalten, ein anderer Rechenweg ist also gut möglich.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Geometrie, Teil A, Aufgabengruppe 2

Volumen der Stufenpyramide

Höhe der Pyramide ABCDSABCDSABCDS

Hast du eine Frage oder Feedback?

Aufstellen der Gerade

Hast du eine Frage oder Feedback?

Abstand der Punkte AAA und BBB

Koordinaten von BBB und CCC

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Höhe der Pyramide $A B C D S$

Abstand der Punkte $A$ und $B$

Koordinaten von $B$ und $C$