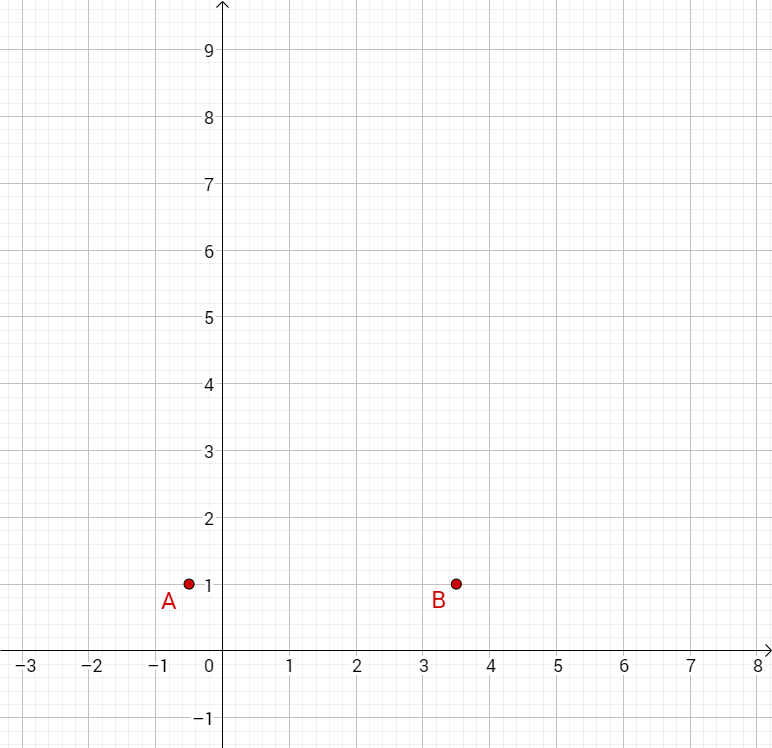
Die Punkte und legen zusammen mit Pfeilen
für Dreiecke fest.
Runden Sie im Folgenden auf eine Stelle nach dem Komma.
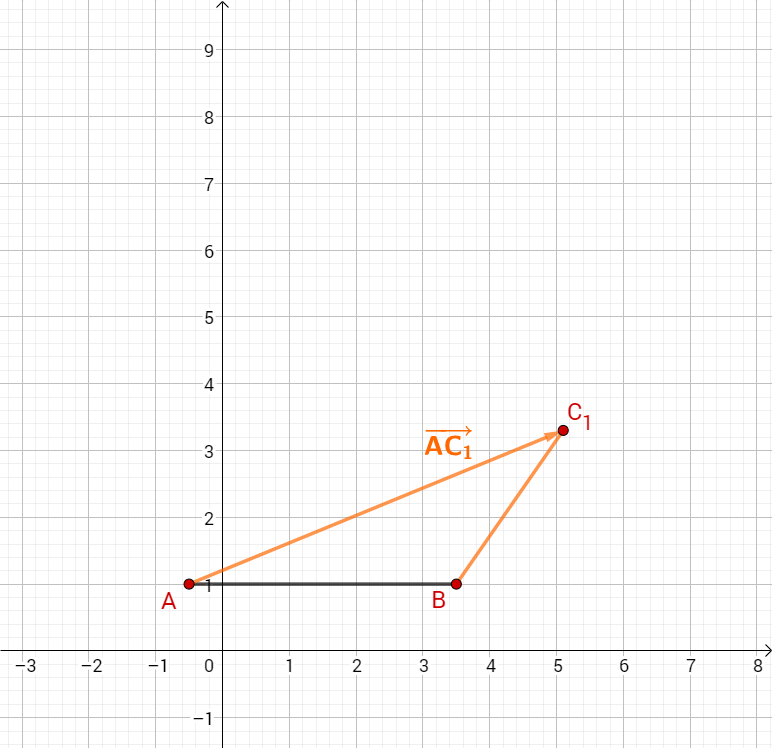
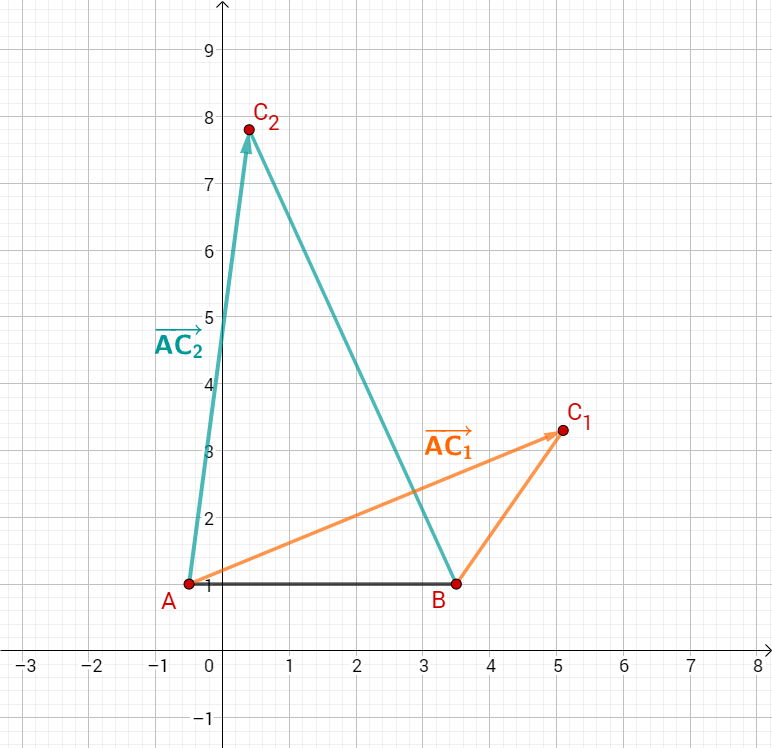
Berechnen Sie die Koordinaten der Pfeile für und für .
Zeichnen Sie anschließend die Dreiecke und in das Koordinatensystem ein.
3 Punkte
Zeigen Sie rechnerisch, dass für die Koordinaten der Punkte in Abhängigkeit von gilt: .
(1 Punkt)
Bestimmen Sie rechnerisch die Gleichung des Trägergraphen der Punkte .
(2 Punkte)
Unter den Dreiecken gibt es das gleichschenklige Dreieck mit der Basis .
Ermitteln Sie das zugehörige Winkelmaß und begründen Sie durch Rechnung, dass das Dreieck nicht gleichseitig ist.
(3 Punkte)