In dieser Teilaufgabe sollst du das Trapez $A_2B_2C_2D$ für $\varphi=40^{\circ}$ in die angegebene Zeichnung einzeichnen. Aus der Aufgabenstellung weißt du, dass die Punkte $D$ und $S$ unter allen Winkeln $\varphi$ festbleiben. Die Länge der Strecke $[A_2B_2]$ ist wieder $4\;\text{cm}$ lang und der Punkt $C_2$ liegt auf derselben Höhe wie $D$.

Um herauszufinden, wo die Punkte $A_2, B_2$ und $C_2$ genau liegen, zeichnest du zuerst den Winkel $\varphi_2 = 40^{\circ}$ mit Hilfe deines Geodreiecks an die Gerade $SD$ ein.

Du weißt, dass $\overline{A_1B_1} = 4\;\text{cm}$ ist, um also $B_2$ zu finden, zeichnest du eine Gerade durch $B_1$ parallel zur Geraden $SD$. Der Schnittpunkt mit der vorherigen Geraden ist $B_2$.

$C_2$ findest du, indem du die Strecke $[DC_1]$ verlängerst.

$A_2$ liegt auf der selben Höhe wie $B_2$ und auf der Geraden $SD$.

In dieser Teilaufgabe sollst du die Streckenlängen $\overline{DC_n}$ und $\overline{SA_n}$ in Abhängigkeit von $\varphi$ darstellen. Diese Art von Aufgaben erscheinen durch ihre Schreibweise und der Anzahl an unbekannten Variablen anfangs immer sehr schwierig. Es empfiehlt sich daher, dass du dich Schritt für Schritt mit deinem Wissen und den bekannten Informationen versuchst heranzutasten.

Zu $\overline{DC_n}$:

Es soll gelten: $\overline{DC_n}(\varphi)=3\cdot tan(\varphi)\;\text{cm}$.

Wenn du genau hinschaust, stellst du fest, dass alle drei Größen, $[DC_n], \overline{SD} =3\;\text{cm}$ und $\varphi$ in deiner gesuchten Gleichung in dem oberen Dreieck auftauchen ($\varphi$ wird mit dem Tangens operiert).

Da du den Tangens kennst, solltest du ihn für dieses rechtwinklige Dreieck mal aufstellen:

$\tan(\varphi)=\dfrac{\overline{DC_n}}{\overline{SD}}=\dfrac{\overline{DC_n}}{3\;\text{cm}}$

Jetzt lässt sich die Lösung bereits erahnen, multipliziere beide Seiten mit $3\;\text{cm}$.

$\Rightarrow \overline{DC_n}=3\;\text{cm}\cdot tan(\varphi)$

Du wunderst dich vielleicht noch, warum in der Aufgabenstellung hinter dem $\overline{DC_n}$ ein ($\varphi$) steht. Dies zeigt dir den funktionellen Zusammenhang zwischen dem Winkel und der Länge der Strecke $[DC_n]$.

Stell dir eine beliebige Funktion vor, z.B.: $f(x)=x + 3$

Links siehst du, in welche Variable du die Zahlen einsetzt, nämlich $x$, da diese "unbekannt" ist. So kannst du es dir auch in unserer Aufgabe vorstellen, denn der Winkel ist unbekannt und variiert (siehe Aufgabe A 1.1 ), dementsprechend verändert sich die Länge der Strecke $[DC_n]$.

Du erhältst also eine Funktion: $\overline{DC_n}(\varphi)=3\;\text{cm}\cdot \tan(\varphi)$

Zu $\overline{SA_n}$:

Es soll gelten: $\overline{SA_n}(\varphi)=\dfrac{4\;\text{cm}}{\tan(\varphi)}$.

Diese Aufgabe funktioniert ähnlich, wieder siehst du, dass du den Tangens benutzen sollst, also stellst du diesen auch hier am besten einfach mal auf.

Suche dir dazu die Größen, die in deiner gesuchten Gleichung auftauchen, dann wirst du feststellen, dass es sich um das große Dreieck handelt.

$\tan(\varphi)=\dfrac{\overline{A_nB_n}}{\overline{SA_n}}=\dfrac{4\;\text{cm}}{\overline{SA_n}}$

Löse auch hier wieder nach der gesuchten Größe auf. Multipliziere daher zuerst beide Seiten mit $\overline{SA_n}$

$\Rightarrow \tan(\varphi)\cdot \overline{SA_n}=4\;\text{cm}$

Um $\overline{SA_n}$ alleine auf der linken Seite zu erhalten, dividiere durch $\tan(\varphi)$

$\Rightarrow \overline{SA_n}=\dfrac{4\;\text{cm}}{\tan(\varphi)}$

Auch hier gilt wieder der funktionelle Zusammenhang, daher erhältst du am Ende

$\overline{SA_n}(\varphi)=\dfrac{4\;\text{cm}}{\tan(\varphi)}$.

In dieser Aufgabe geht es um Berechnungen an dreidimensionalen Körpern.

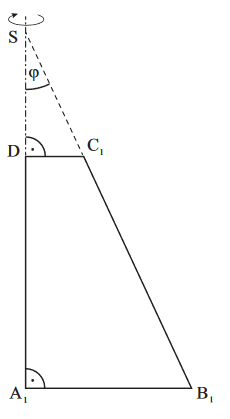
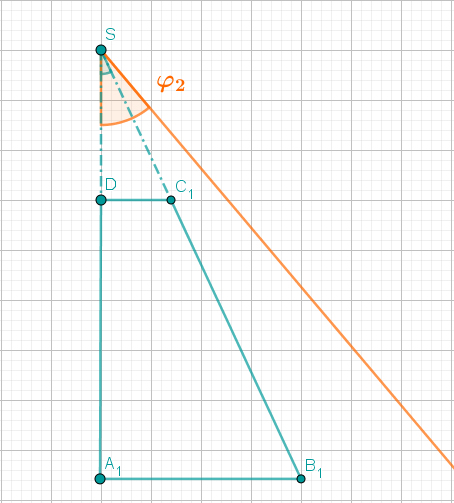
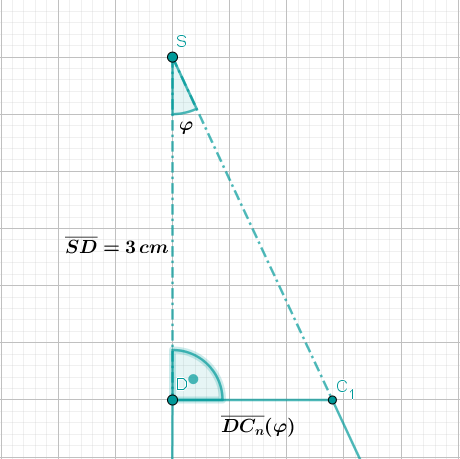
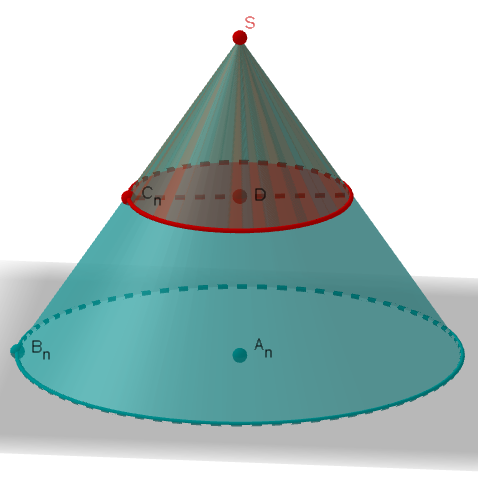
Überlege dir, welche dreidimensionale Figur entsteht, wenn das Dreieck $SA_nB_n$ um die Achse $\overline{SA_n}$ rotiert. Mit etwas räumlichem Vorstellungsvermögen erkennst du, dass ein Kegel entsteht.

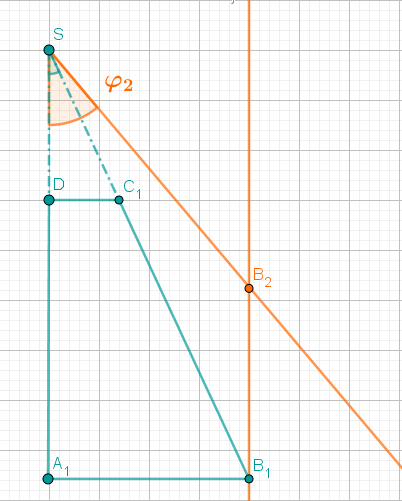
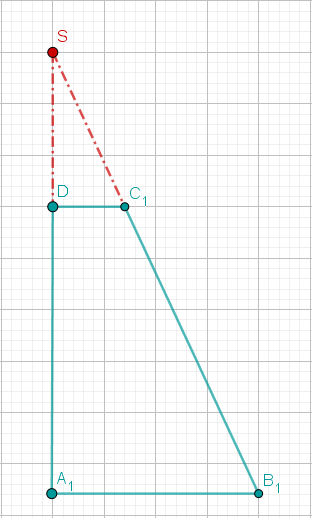
Die Schwierigkeit besteht jedoch darin zu erkennen, dass die Spitze des Kegels nicht zu unserem Volumen gehört, da unsere Grundfläche ein Trapez und kein Dreieck ist.

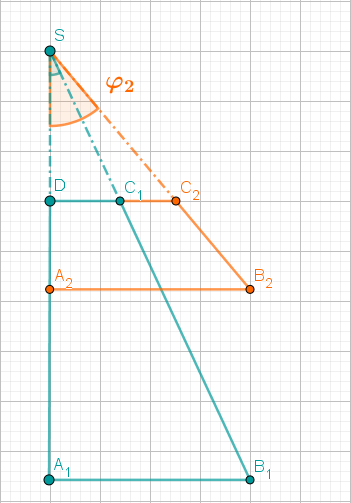
Der gesuchte Rotationskörper ist die entstehende blaue Figur, der rote Bereich wird dabei nicht mitgezählt, es entsteht ein sogenannter Kegelstumpf. Dennoch gestaltet sich die Berechnung des Volumens am leichtesten, wenn du zunächst das Volumen des großen Kegels $SA_nB_n$ berechnest und dann das Volumen des kleineren Kegels $SDC_n$ abziehst.

Wie du weißt, berechnet sich das Volumen eines Kegels mit:

$V_{Kegel}=\dfrac{1}{3} \cdot G \cdot h = \dfrac{1}{3} \cdot r^2 \cdot \pi \cdot h$

Versuche nun, diese Formel auf unsere Figuren anzuwenden.

$V_{SA_nB_n}=\dfrac {1}{3} \cdot \overline{A_nB_n}^2 \cdot \pi \cdot\overline{SA_n}$

$V_{SDC_n}=\dfrac {1}{3} \cdot \overline{DC_n}^2 \cdot \pi \cdot\overline{SD}$

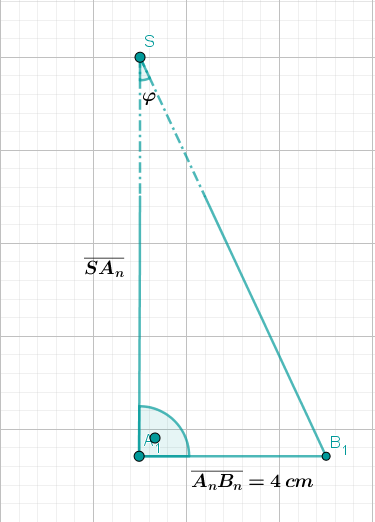
Aus der Angabe weißt du, dass $\overline{A_nB_n}=4\;\text{cm}$ und $\overline{SD} = 3\;\text{cm}$

Aus Teilaufgabe (b) weißt du, dass $\overline{SA_n}=\dfrac{4\;\text{cm}}{\tan(\varphi)}$ und $\overline{DC_n}=3\;\text{cm}\cdot \tan(\varphi)$

Aus der Aufgabenstellung in Teilaufgabe (c) kannst du bereits erahnen, dass du dies einsetzen musst, da in der finalen Formel der Tangens vorkommen muss!

Setze nun alle bekannten Größen in die Volumenformeln ein:

$V_{SA_nB_n}=\dfrac {1}{3} \cdot 16\;\text{cm}^2 \cdot \pi \cdot\dfrac{4\;\text{cm}}{\tan(\varphi)}$

$V_{SDC_n}=\dfrac {1}{3} \cdot (3\;\text{cm}\cdot \tan(\varphi))^2 \cdot \pi \cdot 3\;\text{cm}$

Um also auf das gesuchte Volumen $V(\varphi)$ des Kegelstumpfes in Abhängigkeit von $\varphi$ zu kommen, musst du noch das Volumen des kleinen Kegels vom Volumen des großen Kegels abziehen.

$V(\varphi)=\dfrac {1}{3} \cdot 16\;\text{cm}^2 \cdot \pi \cdot\dfrac{4\;\text{cm}}{\tan(\varphi)} - \dfrac {1}{3} \cdot (3\;\text{cm}\cdot \tan(\varphi))^2 \cdot \pi \cdot 3\;\text{cm}$

In der Aufgabenstellung siehst du, dass $\dfrac{1}{3} \cdot \pi$ ausgeklammert wurde, daher solltest du dies auch jetzt schon tun, um dich in der Rechnung nicht zu verwirren!

$V(\varphi)=\dfrac {1}{3} \cdot \pi \cdot \left(16\;\text{cm}^2 \cdot\dfrac{4\;\text{cm}}{\tan(\varphi)} - (3\;\text{cm}\cdot \tan(\varphi))^2 \cdot 3\text{cm}\right)$

Schließlich verrechnest du alle Zahlen in der Klammer und hängst die Einheit $\text{cm}^3$ hinten an.

$V(\varphi)=\dfrac {1}{3} \cdot \pi \cdot \left(\dfrac{64}{\tan(\varphi)} - 27\cdot \tan(\varphi)^2\right)\,\text{cm}^3$

Wenn du möchtest, kannst du dir im folgenden Video noch eine Schritt-für-Schritt-Lösung der Aufgabe anschauen.