Eine Tangente an einem Graphen ist eine Gerade, die den Graphen einer Funktion an einer bestimmten Stelle berührt und dort dieselbe Steigung wie die Funktion besitzt.
Der Funktionsterm einer Tangente wird entweder durch die Tangentenformel aufgestellt oder durch das schrittweise Konstruieren einer Gerade.
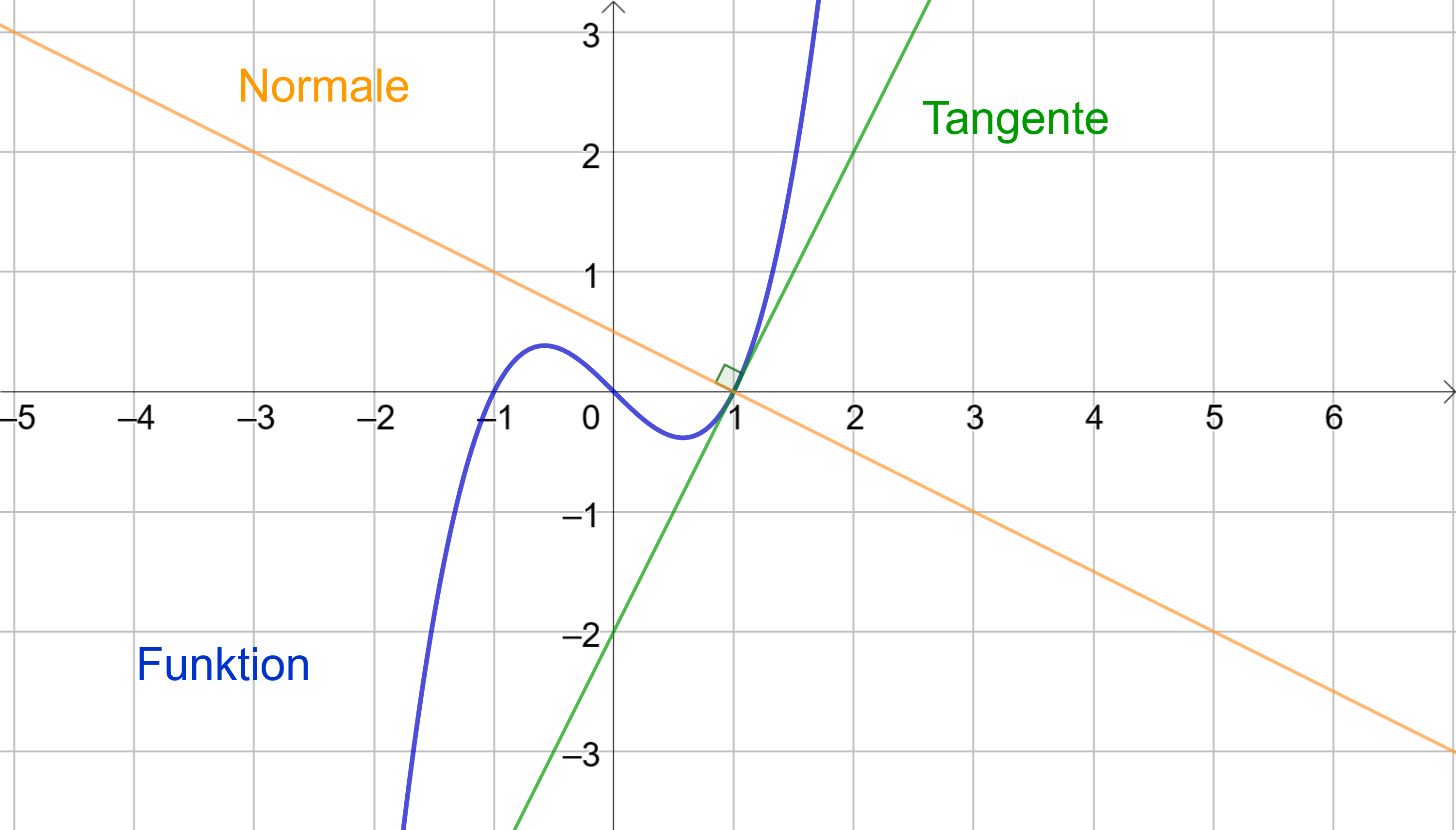
Die Tangentenformel
Die Tangente wird durch einen linearen Funktionsterm angegeben und kann mithilfe der Tangentenformel aufgestellt werden:
Konstruieren aus einer Geraden
Eine Tangente kann auch ohne Formel aufgestellt werden. Da es sich um eine lineare Funktion handelt, lautet deren allgemeine Form:
Die Steigung wird durch die Steigung der Funktion an der Stelle bestimmt, siehe Beispiel. Der y-Achsenabschnitt wird durch eine weitere Information, in Form einer Gleichung, berechnet.
Bestimmung der Tangentengleichung
Tangente für eine gegebene -Koordinate bestimmen
Allgemeines Rezept | Beispiel |
|---|---|
Gegeben ist die Funktion mit dem Term . Bestimme die Gleichung der Tangente an der Stelle . | |
Schreibe die allgemeine Geradengleichung auf. |
: Steigung : y-Achsenabschnitt |
Berechne die Ableitung |
|
Setze den x-Wert in die Ableitung ein, um die Steigung zu erhalten. | |
Setze die Steigung in die allgemeine Geradengleichung ein. | |
Berechne die y-Koordinate, die zur angegebenen x-Koordinate gehört. Setze dazu den x-Wert in den Term der Funktion ein. |
|
Setze die Koordinaten des Berührpunktes in die Geradengleichung ein und löse nach b auf. |
|
Die Tangentengleichung hat die Form: |
|
Berechnung mit der Tangentenformel
Die Funktion wird in von einer Tangente berührt. Wir bestimmen deren Funktionsterm .
Allgemein | Beispiel |
|---|---|
berechnen |
|
bestimmen |
|
berechnen |
|
in Formel einsetzen |
|
Funktionsterm vereinfachen |
|
Der Funktionsterm der Tangente ist also:
Beispiel: Beide Berechnungsmethoden im Überblick
Um den Funktionsterm einer Tangente zu bestimmen, stehen zwei Methoden zur Auswahl: Das Aufstellen mittels Tangentenformel, sowie dem Konstruieren einer Geraden durch das Lösen von Gleichungen. Hier wird beides gegenübergestellt.
Gesucht wird die Tangente, die den Funktionsgraphen von an der Stelle berührt.
Tangentenformel | Gerade konstruieren |
|---|---|
Schreibe zunächst die Formel auf: | Schreibe den allgemeinen Funktionsterm einer Gerade auf: |
Bestimme die 1. Ableitung von : | Bestimme die 1. Ableitung von : |
Berechne : | Berechne , also : |
Setze die Steigung in die Gleichung ein: | |
Bestimme : | Bestimme : |
Damit folgt, dass die Tangente durch den Punkt verläuft. Setze den Punkt in den Funktionsterm ein und löse nach auf: | |
Setze in die Tangentenformel ein und vereinfache: | Setze und in die Geradegleichung ein: |
Die Verfahren liefern beide den gleichen Funktionsterm, womit also frei gewählt werden kann, wie eine Tangente aufgestellt wird. Welche Methode den geringeren Aufwand betreibt, muss von einem selbst beurteilt werden.
Beispiel: Tangente mit gegebener Steigung
Allgemeines Rezept | Beispiel |
|---|---|
Gegeben ist die Funktion . Berechne die Tangente(n) mit der Steigung . | |
Stelle die allgemeine Geradengleichung auf. | : Steigung : y-Achsenabschnitt |
Berechne die Ableitung. |
|
Setze die Ableitung mit der Steigung gleich und löse nach auf. |
|
Setze den -Wert in die Funktion ein, um einen Punkt zu erhalten. |
|
Setze den -Wert, -Wert und die Steigung in die allgemeine Geradengleichung ein und löse nach auf. |
|
Die Tangentengleichung lautet also: |
Die Wendetangente
Die Wendetangenten einer Funktion sind die Tangenten an ihren Wendepunkten. Eine Funktion kann demnach eine, mehrere oder auch keine Wendetangenten besitzen, abhängig davon wie viele Wendepunkte sie besitzt.
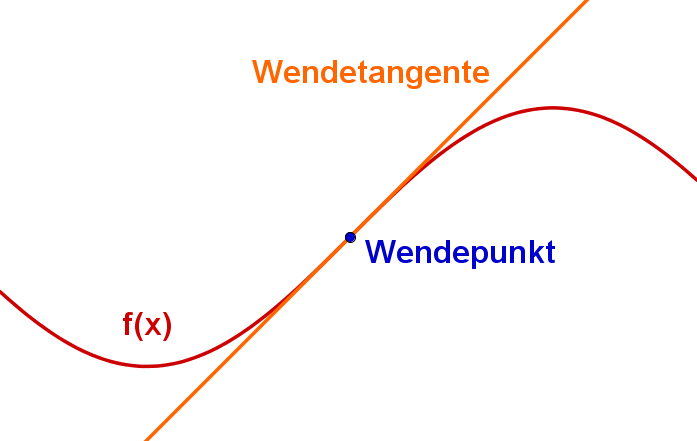
Beispiel einer Wendetangente
Berechne alle Wendetangenten der Funktion
Allgemeines Rezept | Beispiel |
|---|---|
Zur Berechnung der Wendepunkte benötigt man die ersten drei Ableitungen. |
|
Alle möglichen Wendepunkte erfüllen , man benötigt also die Nullstellen der zweiten Ableitung. |
|
Die quadratische Gleichung wird mit der abc-Formel gelöst. |
|
Man muss diese Stellen noch in die dritte Ableitung einsetzen, um zu überprüfen, ob hier Wendepunkte vorliegen. |
|
Da beide Stellen eine dritte Ableitung ungleich Null besitzen, liegt an beiden Stellen ein Wendepunkt vor. Zur Berechnung der Tangenten benötigt man noch den Funktionswert und den Wert der Ableitung an den entsprechenden Stellen. |
|
Einsetzen in die allgemeine Tangentengleichung ergibt die beiden Wendetangenten . |
|
Das Auflösen der Klammern zeigt die Form der gewöhnlichen Geradengleichung. |
|
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
