Gegeben sind die in definierte Funktion mit sowie die Punkte für . Die Abbildung zeigt den Graphen von sowie die Punkte und .
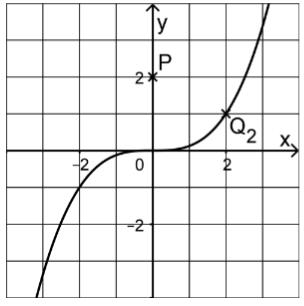
Berechnen Sie für die Steigung der Gerade durch die Punkte und in Abhängigkeit von an. (2P)
(zur Kontrolle: )
Die Tangente an den Graphen von im Punkt wird mit bezeichnet. Bestimmen Sie rechnerisch denjenigen Wert von , für den durch verläuft. (3P)
