Analysis, Teil B, Aufgabengruppe 1

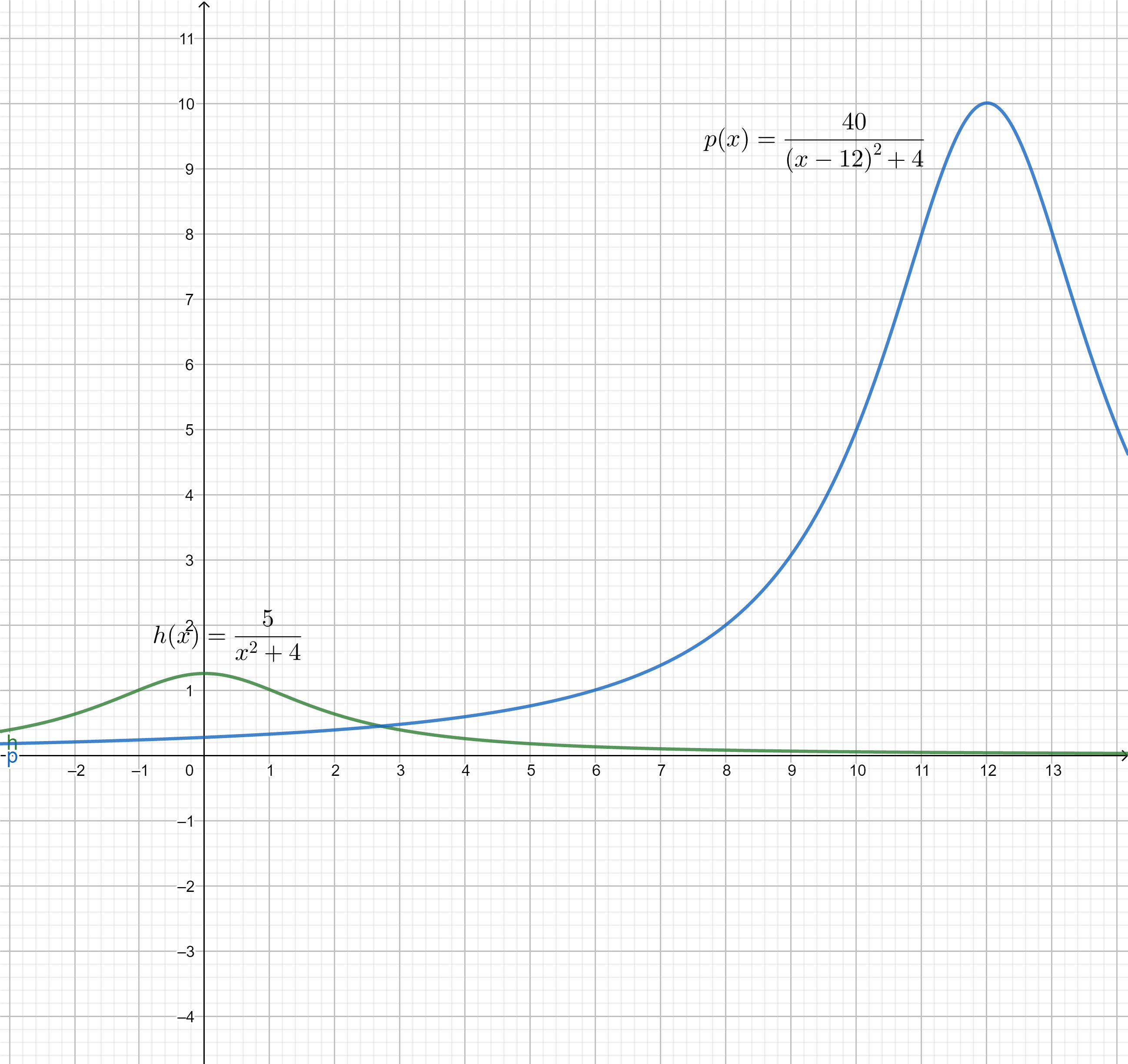
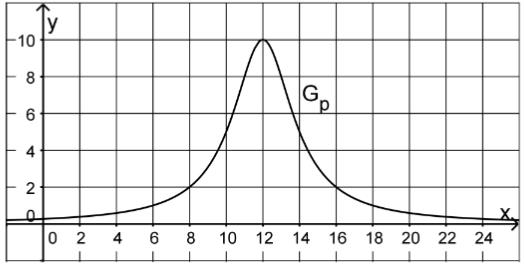
Betrachtet wird die in $\mathbb{R}$ definierte Funktion $p:x \mapsto\dfrac{40}{(x-12)^2+4}$ ; die Abbildung zeigt den Graphen $G_{p}$ von p.

Beschreiben Sie, wie $G_{p}$ aus dem Graphen der in $\mathbb{R}$ definierten Funktion $h:x\mapsto\dfrac{5}{x^2+4}$ schrittweise hervorgeht, und begründen Sie damit, dass $G_{p}$ bezüglich der Gerade mit der Gleichung $x = 12$ symmetrisch ist. (4P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsgraphen verändern
Ausgehend vom Graphen $G_{h_{}}$ der Funktion $\displaystyle h(x)=\frac{5}{x^2+4}$ h soll der Graph $G_{p}$ der Funktion $\displaystyle p(x) =\frac{40}{(x-12)^2+4}$ dargestellt werden.
Der Graph $G_{f}$ der Funktion $y = f (x - a); a > 0$ ergibt sich aus dem Graphen $G_{g}$ der Funktion $g (x) = f (x - a)$ durch Verschiebung um $a$ in Richtung der positiven $x -$ Achse.
Beispiel: Der Graph der Funktion $f_{o} (x) = x^{2}$ ist die Normalparabel mit dem Scheitelpunkt $S_{o} (0 ∣ 0)$ und der Graph der Funktion $f_{a} (x) = (x - a)^{2}$ ist die um $a$ in Richtung der positiven $x -$ Achse verschobene Normalparabel mit dem Scheitelpunkt $S_{a} (a ∣ 0)$ .
Ersetzt man in der Funktion $h$ die unabhängige Variable $x$ durch $x - 12$ , so erhält man $\displaystyle h_{12}(x)=\frac{5}{(x-12)^2+4}$ .
Der Graph $G_{h_{12}}$ ergibt sich aus dem Graphen $G_{h}$ durch Verschiebung um $12 \thinspace LE$ in Richtung der positiven $x -$ Achse.
Multipliziert man $h_{1} (x)$ mit dem Faktor $8$ , so werden alle Funktionswerte um den Faktor $8$ vergrößert. Man erhält den Graphen $G_{p}$
$8\cdot h_1(x)=8\cdot \frac{5}{(x-12)^2+4}=\frac{40}{(x-12)^2+4}=p(x)$
Der Graph $G_{h}$ ist achsensymmetrisch bzgl. der $y -$ Achse, weil sowohl Zählerterm als auch Nennerterm von $h$ gerade sind.
Es gilt: $h(x)=h(-x)\thinspace \forall x\in \mathbb{R}.$
Also ist der Graph $G_{h}$ symmetrisch zur Geraden mit der Gleichung $x = 0$ .
Weil man $x$ durch $x - 12$ ersetzt hat, ist der Graph $G_{p}$ symmetrisch zur Geraden mit der Gleichung $x = 12.$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Eine auf einem Hausdach installierte Photovoltaikanlage wandelt Lichtenergie in elektrische Energie um. Für $4 \leq x \leq20$ beschreibt die Funktion p modellhaft die zeitliche Entwicklung der Leistung der Anlage an einem bestimmten Tag. Dabei ist $x$ die seit Mitternacht vergangene Zeit in Stunden und $p (x)$ die Leistung in kW (Kilowatt).
Bestimmen Sie rechnerisch die Uhrzeit am Nachmittag auf Minuten genau, ab der die Leistung der Anlage weniger als $40$ % ihres Tageshöchstwerts von $10$ kW beträgt. (4P)

Für diese Aufgabe benötigst Du folgendes Grundwissen: Ungleichungen lösen
Die Leistung der PV-Anlage wird modellhaft durch die Funktion $p^{}$ beschrieben.
$p(x)=\dfrac{40}{(x-12)^2+4}$
Für welches $x$ gilt: $p (x) < 4$
$\dfrac{40}{(x-12)^2+4}<4\iff \dfrac{10}{(x-12)^2+4}<1\iff 10<(x-12)^2+4\\\iff 6<(x-12)^2\iff \sqrt{6}<|x-12|$
Diese Ungleichung bedeutet, welche Werte von $x$ haben von $12$ einen Abstand, der größer als $\sqrt{6}$ ist?
Da in der Aufgabe nach einer Uhrzeit am Nachmittag gefragt ist, gilt:
$\sqrt{6}<x-12\iff x > 12+\sqrt{6}\iff x > 12+2{,}449\\\Rightarrow x>14 \thinspace$ Uhr $27 \thinspace$ Minuten
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die Funktion $p$ besitzt im Intervall $[4; 12]$ eine Wendestelle. Geben Sie die Bedeutung dieser Wendestelle im Sachzusammenhang an. (2P)

Die Funktion $p$ ist im Intervall $\left[4;12\right]$ monoton steigend, denn
$\displaystyle p'(x)=40\cdot\frac{-2\cdot(x-12)}{[(x-12)^2+4)]^2}=-80\cdot\frac{x-12}{[(x-12)^2+4]^2}>0$ .
Da der Nennerterm von $p^{'} (x)$ als Quadrat positiv ist und der Zählerterm $-80\cdot (x-12)$ im Intervall $[4; 12]$ auch positiv ist, wächst $p$ im Intervall $[4; 12]$ .
Der Wendepunkt ist ein (möglicher) Extrempunkt der 1. Ableitung, also der Veränderung (hier: Ansteigen) der Leistung.
Bis zur Wendestelle $x_{w}$ wird das Ansteigen der Leistung immer stärker und nach der Wendestelle wird das Ansteigen schwächer. An der Wendestelle hat das Ansteigen der Leistung seinen Maximalwert erreicht. Um $12\thinspace$ Uhr hat das Ansteigen den Wert Null.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Die von der Anlage produzierte elektrische Energie wird vollständig in das Stromnetz eingespeist. Der Hauseigentümer erhält für die eingespeiste elektrische Energie eine Vergütung von $10$ Cent pro Kilowattstunde (kWh). Die in $[4; 20]$ definierte Funktion $x\mapsto E(x)$ gibt die elektrische Energie in kWh an, die die Anlage am betrachteten Tag von $4 : 00$ Uhr bis $x$ Stunden nach Mitternacht in das Stromnetz einspeist.
Es gilt $E^{'} (x) = p (x)$ für $x \in[4;20]$ .
Bestimmen Sie mithilfe der Abbildung einen Näherungswert für die Vergütung, die der Hauseigentümer für die von $10 : 00$ Uhr bis $14 : 00$ Uhr in das Stromnetz eingespeiste elektrische Energie erhält. (3P)

Die in $\left[4{,}20\right]$ definierte Funktion $x\to E\left(x\right)$ gibt die eingespeiste elektrische Energie an und es gilt $E'\left(x\right)=p\left(x\right).$ Somit ist $E$ Stammfunktion von $p .$
Und mittels $\int_{10}^{14}p(x)dx$ berechnet sich die eingespeiste Energie von $10 : 00$ Uhr bis $14 : 00$ Uhr.
$\int_{10}^{14}p(x)dx$ lässt sich näherungsweise über den Inhalt der dem Graph von $p (x)$ einbeschriebenen Treppenfigur $U$ bzw. umbeschriebenen Treppenfigur $O$ berechnen.
Da der Graph von $p (x)$ symmetrisch bzgl. der $y -$ Achse ist, genügt es, den Inhalt der Treppenfiguren im Intervall $[10; 12]$ zu berechnen. Den dann berechneten Wert des Flächeninhaltes multipliziert man mit $2.$
Man unterteilt das Intervall $[10,12]$ in zwei Teilintervalle der Länge $\Delta x=1$ .
Es gilt: $p(10)=\frac{40}{(10-12)^2+4}=5;\quad \quad \thinspace p(11)=\frac{40}{(11-12)^2+4}=8; \quad \quad \thinspace p(12)=10$
Dann erhält man für die Fläche der einbeschriebenen Treppenfigur
$U=5\cdot 1+8\cdot 1=13\thinspace \text{FE}$
Und für die Fläche der umbeschriebenen Treppenfigur:
$O=8\cdot 1+10\cdot 1=18\thinspace \text{FE}$
Bildet man den Mittelwert von $U$ und $O$ , so erhält man: $\frac{U+O}{2}=\frac{31}{2}\thinspace \text{FE}$
Somit kann man den Wert des Flächeninhaltes unter dem Graph von $p (x)$ im Intervall $[10; 14]$ näherungsweise mit $31 \thinspace \text{FE}$ angeben.
Damit werden in der Zeit von $10 : 00$ Uhr bis $14 : 00$ Uhr etwa $31\thinspace \text{kWh}$ eingespeist.
Der Hauseigentümer erhält als Vergütung $3{,}10\thinspace$ Euro.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?