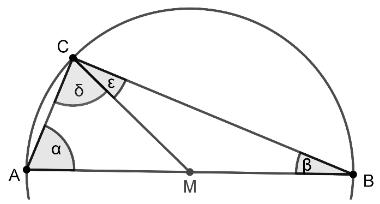
Die Eckpunkte des Dreiecks liegen auf einem Kreis, dessen Mittelpunkt auch der Mittelpunkt der Seite ist. Um zu beweisen, dass ein solches Dreieck bei einen rechten Winkel hat, wird das Dreieck durch die Strecke in zwei Teildreiecke zerlegt.
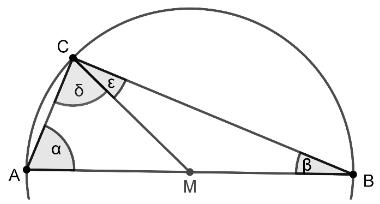
Zunächst soll bewiesen werden, dass gilt (vgl. Abbildung). Dazu müssen die folgenden Aussagen in die richtige Reihenfolge gebracht werden.
I. Das Dreieck ist gleichschenklig mit Basis AC.
II. und liegen auf einem Kreis um .
III.
IV.
III.
Ebenso lässt sich zeigen, dass gilt. Zeige, dass aus und mithilfe der Innenwinkelsumme im Dreieck folgt, dass gilt. Damit ist obige Aussage (Satz des Thales) bewiesen.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?