Gruppe A

Die Aufgaben findest du hier zum Ausdrucken als PDF

1
Berechne:
1. $(-7)^2=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzen
  $(-7)^2=(-7)\cdot(-7)=49$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Multipliziere die Zahl mit sich selbst. Beachte das Vorzeichen.
2. $3^{-2}=$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Potenzgestze
  $\ 3^{-2}=\dfrac{1}{3^2}=\dfrac{1}{9}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Schreibe die Zahl als Bruch. Verwende das Potenzgesetz $\ \ a^{-x}=\dfrac1{a^x}$
2
Betrachtet wird die folgende Rechenanweisung: „Denke dir eine natürliche Zahl. Verdopple sie und subtrahiere vom Ergebnis 3. Multipliziere die Zahl, die du nach dieser Rechnung erhältst, mit 5 und addiere anschließend 15.“
1. Jakob denkt sich die Zahl 9 und rechnet richtig. Gib sein Endergebnis an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Terme aufstellen
  $\ 9\cdot2$
  $\ 9\cdot2-3$
  $\ (9\cdot2-3)\cdot15$
  $\ (9\cdot2-3)\cdot15+15$
  Berechne den Term:
  $\ (9\cdot2-3)\cdot15+15=(18-3)\cdot5+15=15\cdot5+15=90$
  Jakob kommt als Ergebnis auf die Zahl $\ \boxed{90}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Verdopple $9$
  Subtrahiere $3$
  Multipliziere das Ergebnis mit $5$
  Addiere $15$
2. Stelle in Abhängigkeit von der gedachten Zahl n einen allgemeinen Term auf, der die Rechenanweisung beschreibt. Vereinfache anschließend deinen Term so weit wie möglich.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Term
  $\ (2\cdot n-3)\cdot5+15\$ löse die Klammer auf
  $\ 10n-15+15=10n$
  Der gesuchte Term lautet: $\ \boxed{\large{\text{10n}}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Folge der Anweisung der Teilaufgabe $\text{2a}$ , ersetze die Zahl $9$ durch $\text{n}$ .

Bestimme für $x \in\mathbb{Q}$ die Lösung der Gleichung

\displaystyle \frac{1}{2}x-2=\frac{1}{2}-x+2x.

4
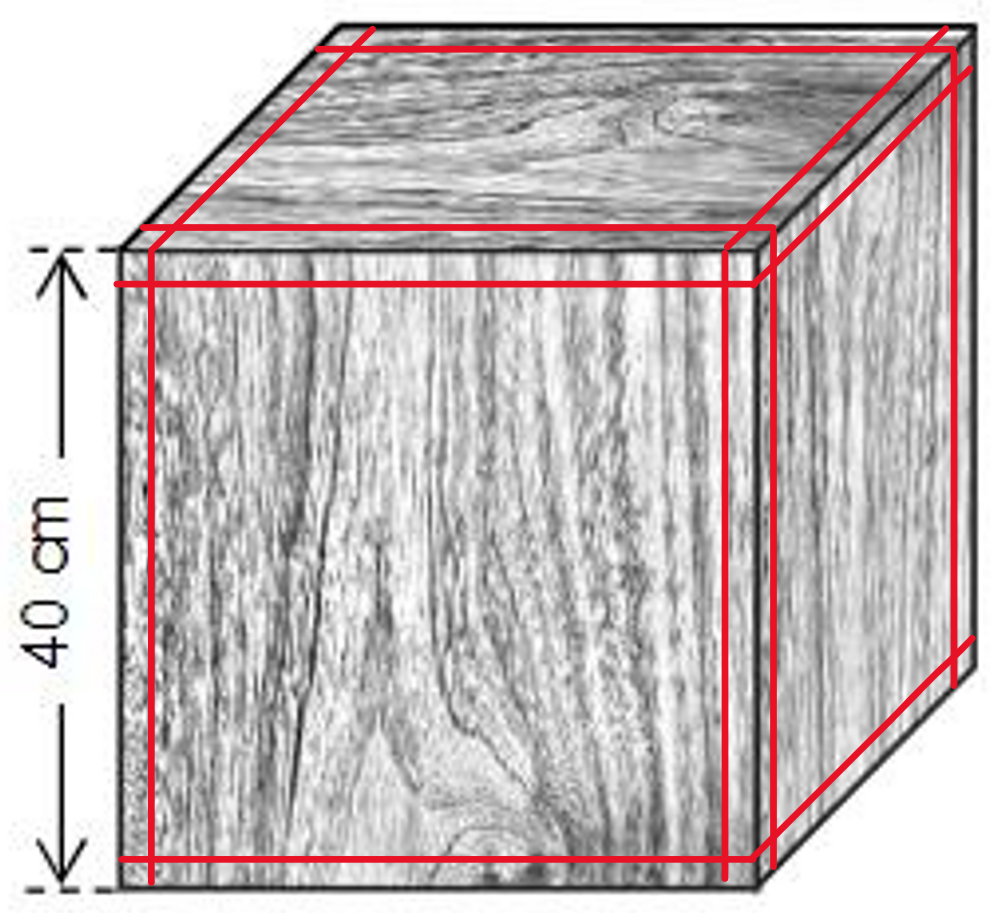
Ein Würfel hat die Kantenlänge 40cm.
1. Berechne das Volumen dieses Würfels in Litern.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Würfel
  Aus der Aufgabenstellung ist bekannt, dass die Seite $a$ des Würfels $40\ cm$ ist.
  Die Formel zur Berechnung des Volumens eines Würfels lautet:
  $\ V_{\text{Würfel}}=a^3\Rightarrow V_{\text{Würfel}}=(40\ cm)^3$
  $\ V_{\text{Würfel}}=64000\ \text{cm}^3$
  Das Volumen des Würfels soll in Litern berechnet werden.
  $\ 1\ \text{l}\ \widehat{=}\ 1\ \text{dm}^3;\quad\ 1\ \text{dm}^3=(10\ \text{cm})^3=1000\ cm^3$
  Das Volumen des Würfels in Liter ist also:
  $\ \dfrac{64000\ cm^3}{1000\dfrac{\ cm^3}{l}}=64\ l$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Ein solcher Würfel wurde als Sitzhocker gebaut (vgl. Abbildung). Für die sechs Seitenflächen wurden 1cm dicke Holzbretter verwendet. Innen ist der Sitzhocker hohl.
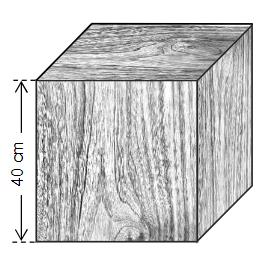
  Das Volumen des verbauten Holzes soll berechnet werden.
  Ein korrekter Ansatz für diese Berechnung ist $(40cm)^3-(40cm-2cm)^3$ .
  Gib die Bedeutung des Subtrahenden $(40cm-2cm)^3$ im Sachzusammenhang an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Würfel
  Da die Bretter eine Dicke von $1\ \text{cm}$ haben gilt für die Seitenlänge
  des inneren hohlen Würfels: $\ 40\ \text{cm}-2\ \text{cm}$ .
  Der Subtrahend beschreibt also das Volumen des inneren hohlen Würfels.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Der Ansatz $6\cdot (40cm)^2\cdot 1cm$ liefert einen Näherungswert für das Volumen des verbauten Holzes. Begründe ohne zu rechnen, dass dieser Näherungswert größer ist als der korrekte Wert.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Würfel
  Der Term stellt das Volumen sechs einzelner Bretter dar. Da diese allerdings zu einem Würfel mit der Kantenlänge $40\ cm$ zusammengefügt wurden, würden jetzt die Ränder doppelt und die Ecken dreifach mitgezählt werden.
  Deshalb liefert der Term einen größeren Wert.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Finde zunächst heraus, welches Volumen dieser Term darstellt. Was wurde eventuell zu viel berechnet?
5
Auf einer Party befinden sich m Mädchen und j Jungen, wobei die Anzahl der Jungen um 20% kleiner ist als die der Mädchen. Zwei der folgenden Gleichungen passen dazu. Kreuze (nur) diese an.
$j=m-\dfrac{20}{100}$
$m=j-\dfrac{20}{100}$
$j=0{,}8m$
$m=0{,}8 j$
$m=20j$
$j=20m$
$m=j-\dfrac{1}{5} j$
$j=m-\dfrac{1}{5} m$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Gleichung aufstellen
Die Anzahl der Jungen ist um $\ 20\%\$ kleiner als die Anzahl der Mädchen, also ist:
$\ j=(100\%-20\%)\cdot m\Rightarrow\ \boxed{j=0{,}8\cdot \text{m}}$ und:
$\hspace{39mm}\ \boxed{j=\text{m}-\dfrac{1}{5}\text{m}}$
Bezeichne die Anzahl der Jungen mit $\ \boxed{\text{j}}\$ und die Anzahl der Mädchen $\ \boxed{\text{m}}\$ .
6
Die Anzahl der in Deutschland pro Person verbrauchten Plastiktüten sank von 68 im Jahr 2015 auf 24 im Jahr 2018 (siehe Abb.).
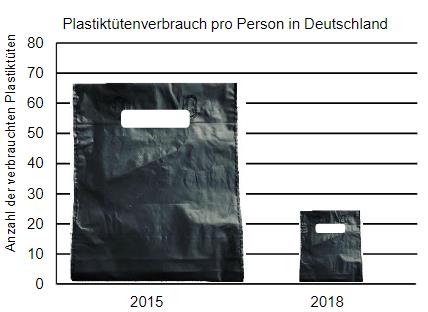
1. Durch die Darstellung in der Abbildung könnte der Eindruck entstehen, dass die Anzahl der pro Person verbrauchten Plastiktüten deutlich stärker gesunken ist als dies tatsächlich der Fall war. Erläutere die Ursache für diesen Eindruck.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Diagramm
  Bei der zweiten Plastiktüte wurde nicht nur die Höhe verringert, sondern auch die Breite, dadurch kann der Eindruck entstehen, der Verbrauch ist deutlich stärker gesunken als das tatsächlich der Fall war.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Im Jahr 2018 wurden in Deutschland etwa 2 Milliarden Plastiktüten verbraucht. Die Dicke der Folie, aus der die Tüten bestehen, beträgt durchschnittlich etwa 0,05mm. In einem Gedankenexperiment werden alle diese Tüten zu einem Stapel übereinander gelegt. Schätze mit einer Rechnung die Höhe dieses Stapels ab. Gib dein Ergebnis in Kilometern an.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Umrechnen von Einheiten
  Dicke Folie: $\quad 0{,}05\ \text{mm}$
  Anzahl Plastiktüten: $\ 2\cdot 10^9$
  a.) Höhe eines Stapels von $\ 2\cdot 10^9\$ Plastiktüten in $\text{[mm]}$
  $\ 2\cdot\ 2\cdot10^9\cdot0{,}05\ \text{mm}=0{,}2\text{mm}\cdot10^9=2\cdot10^8\ \text{mm}$
  b.) Berechnung der Höhe in $\ \text{[km]}$
  $\ 1\ \text{km}=10^6\ \text{mm}\Rightarrow\ 2\cdot10^8\ \text{mm}=2\cdot\dfrac{10^8\ \cancel{\text{{mm}}}}{10^6\dfrac{\cancel{\text{mm}}}{km}\ }=200\ \text{km}$
  Die Höhe des Stapels beträgt $\ \boxed{200\ \text{km}}.$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  a.) Berechne die Höhe des Stapels von Plastiktüten in $\ \text{[mm]}$
  b.) Wandle das Ergebnis von $\ \text{[mm]}\$ in $\ \text{[km]}\$ um.
  
  Beachte, für eine Plastiktüte werden 2 Lagen Folien gebraucht!
3. Durch das Verpackungsgesetz vom 01.01.2019 soll die Recyclingquote von Kunststoffverpackungen, die in Privathaushalten anfallen, um 27 Prozentpunkte von 36 Prozent vor Inkrafttreten des Gesetzes auf 63 Prozent im Jahr 2022 ansteigen. Einer der folgenden Brüche ist gleich dem Prozentsatz, um den diese Recyclingquote ansteigen soll. Kreuze (nur) diesen an
  $\dfrac{27}{36}$
  $\dfrac{100}{36}$
  $\dfrac{36}{63}$
  $\dfrac{27}{63}$
  $\dfrac{27}{100}$
  $\dfrac{36}{100}$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Prozent und Prozentpunkte
  Grundwert $\ \hspace{2.5mm}\text{G}=36$
  Prozentwert $\ \text{W}=63-36=27$
  $\ p=\dfrac{W}{G}\Rightarrow p=\dfrac{27}{36}$
  Der richtige Bruch lautet also: $\ \dfrac{27}{36};\$ kreuze entsprechend an.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme den Grundwert $\ \text{G}\$ und den Prozentwert $\ \text{W}$ .
  Schau dir noch einmal das Kapitel, Prozent und Prozentpunkte, an.
7
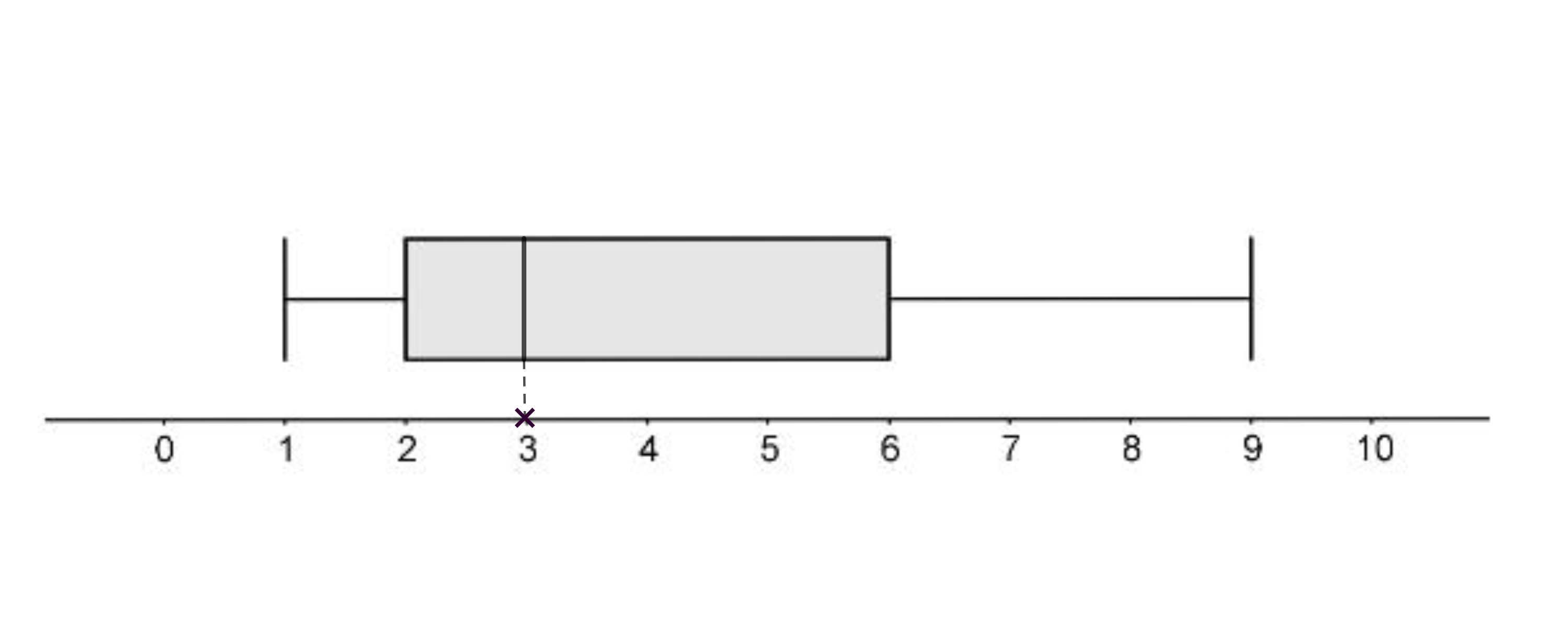
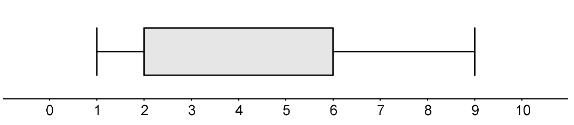
Folgender Datensatz soll in einem Boxplot dargestellt werden: $1;1;2;2;2;2;3;4;4;6;6;7;9$
Vervollständige den Boxplot durch Angabe des fehlenden Medians.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Median
Bestimmung des Medians, da die Zahlen schon der Grösse nach geordnet sind und die Anzahl der Zahlen ungerade ist, kannst du jeweils die beiden äusseren Zahlen streichen, bis eine Zahl übrig bleibt. Diese Zahl ist dann der Median, in diesem Fall ist die Zahl $3$ der Median.
$\hspace{45mm}\cancel{1};1;2;2;2;2;3;4;4;6;6;7;\cancel{9}$
$\hspace{48.5mm}\cancel1;2;2;2;2;3;4;4;6;6;\cancel7\\\hspace{52mm}\cancel2;2;2;2;3;4;4;6;\cancel6\\\hspace{56mm}\cancel2;2;2;3;4;4;\cancel6\\\hspace{59.5mm}\cancel2;2;3;4;\cancel4\\\hspace{63mm}\cancel2;3;\cancel4\\\hspace{66.7mm}3$
Bestimme den Median und kennzeichne ihn im Boxplot.
8
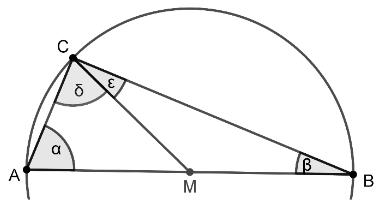
Die Eckpunkte des Dreiecks $ABC$ liegen auf einem Kreis, dessen Mittelpunkt $M$ auch der Mittelpunkt der Seite $\overline{AB}$ ist. Um zu beweisen, dass ein solches Dreieck bei $C$ einen rechten Winkel hat, wird das Dreieck durch die Strecke $\overline{MC}$ in zwei Teildreiecke zerlegt.
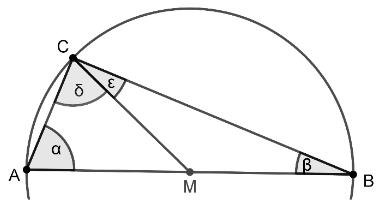
1. Zunächst soll bewiesen werden, dass $\alpha=\delta$ gilt (vgl. Abbildung). Dazu müssen die folgenden Aussagen in die richtige Reihenfolge gebracht werden.
  I. Das Dreieck $AMC$ ist gleichschenklig mit Basis AC.
  II. $A$ und $C$ liegen auf einem Kreis um $M$ .
  III. $\alpha=\delta$
  IV. $|\overline{AM}|=|\overline{CM}|$
  $\square\Rightarrow\square\Rightarrow\square\Rightarrow$ III.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Thales
  $\ \text{II}.\$ $A$ und $C$ liegen auf einem Kreis um $M$ .
  Da $A$ und $C$ auf einem Kreis mit dem Mittelpunkt $M$ liegen,
  ist $|\overline{AM}|\ \text{und}\ |\overline{CM}|$ gleich dem Radius des Kreises. Also ist:
  $\ \text{IV}.$ $\ |\overline{AM}|=|\overline{CM}|$
  Da: $\ \ |\overline{AM}|=|\overline{CM}|$ , ist das Dreieck gleichschenklig. Also ist:
  $\ \text{I}.$ Das Dreieck $\ \text{AMC}\$ ist gleichschenklig mit der Basis $\ \text{AC}.$
  Da das Dreieck gleichschenklig ist, sind die beiden
  Basiswinkel $\ \alpha\$ und $\ \delta\$ gleich. Also ist:
  $\ \text{III}.\ \alpha=\delta$
  Die richtige Reihenfolge sieht dann so aus:
  $\ \boxed{\text{II}}\Rightarrow\boxed{\text{IV}}\Rightarrow\boxed{\text{I}}\Rightarrow\boxed{\text{III}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bringe die Aussagen in die richtige Reihenfolge, indem du mit Aussage $\ \text{II}\$ beginnst.
2. Ebenso lässt sich zeigen, dass $\beta=\epsilon$ gilt. Zeige, dass aus $\alpha=\delta$ und $\beta=\epsilon$ mithilfe der Innenwinkelsumme im Dreieck $ABC$ folgt, dass $\delta+\epsilon=90°$ gilt. Damit ist obige Aussage (Satz des Thales) bewiesen.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Satz des Thales
  Innenwinkelsumme im Dreieck ABC:
  $\alpha+\delta+\epsilon+\beta= 180°$
  aus $\ \alpha=\delta\$ und $\ \beta=\epsilon$
  $\Rightarrow 2\delta+2\epsilon=180°\ |:2$
  $\hspace{7mm}\boxed{\delta+\epsilon=\ 90°}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte: Die Dreiecke $\ \text{AMC}\$ und $\text{CMB}\$ sind gleichschenklige Dreiecke.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle \frac{1}{2}x-2$	$=$	$\displaystyle \dfrac{1}{2}-x+2x$	$\displaystyle \ \cdot2$
$\displaystyle x-4$	$=$	$\displaystyle 1-2x+4x$	$\displaystyle \ +2x-4x$
$\displaystyle x+2x-4x-4$	$=$	$\displaystyle 1$	$\displaystyle \ +4$
$\displaystyle x+2x-4x$	$=$	$\displaystyle 5$
	↓	Fasse zusammen
$\displaystyle -x$	$=$	$\displaystyle 5$	$\displaystyle \ \cdot(-1)$
$\displaystyle x$	$=$	$\displaystyle -5$

Gruppe A

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?