Der Graph einer auf definierten ganzrationalen Funktion f vom Grad drei verläuft durch den Punkt und besitzt im Schnittpunkt mit der y-Achse einen Wendepunkt. Für die Wendetangente gilt: mit der Definitionsmenge .
Stellen Sie eine Funktionsgleichung von f auf.
(Mögliches Teilergebnis: ) (6 BE)
Bestimmen Sie jeweils Art und Koordinaten der relativen Extrempunkte von und begründen Sie, warum f nur eine einfache Nullstelle besitzt. (8 BE)
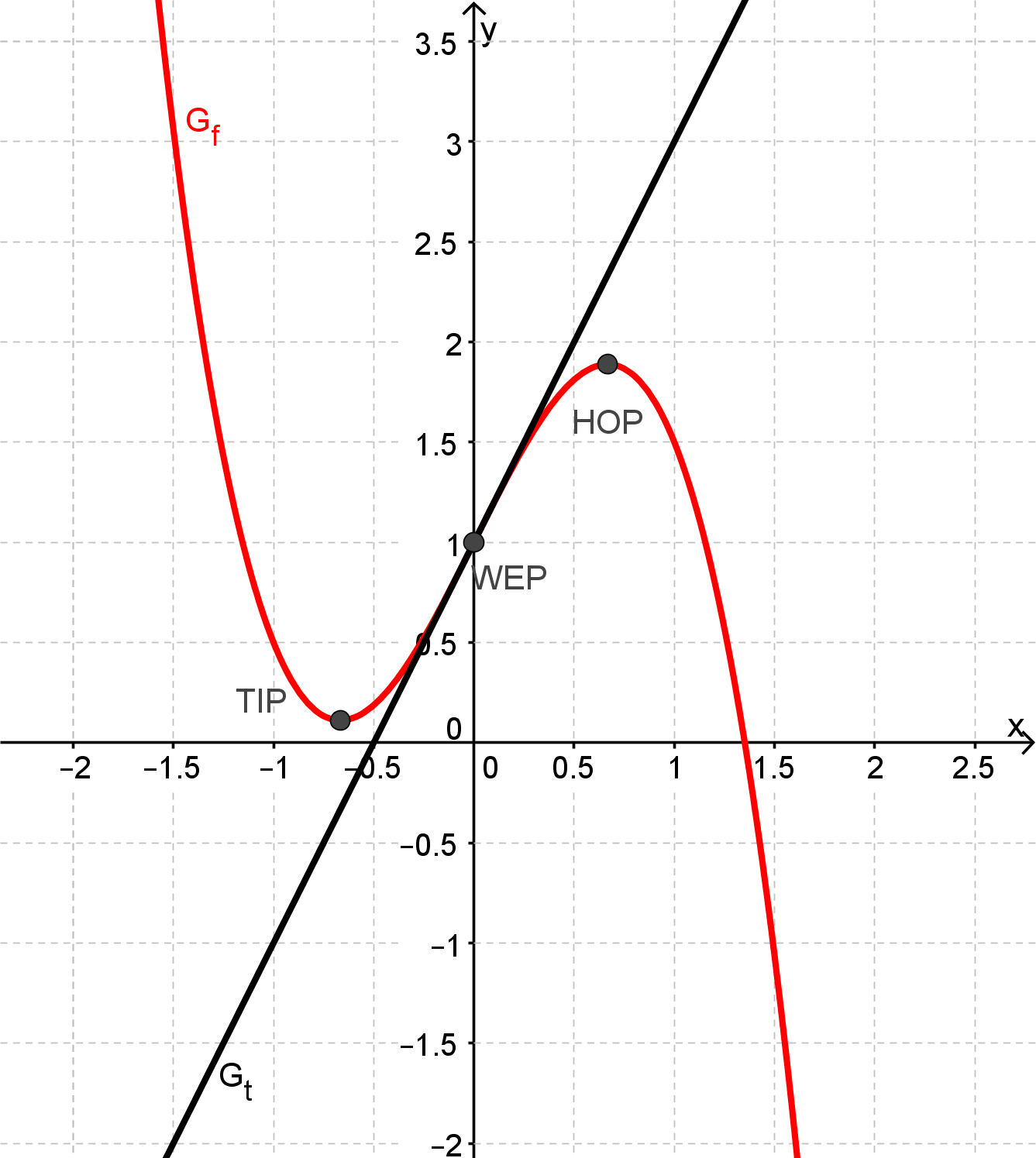
Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den Graphen und die Tangente im Bereich in ein kartesisches Koordinatensystem.
Maßstab für beide Achsen: (5 BE)
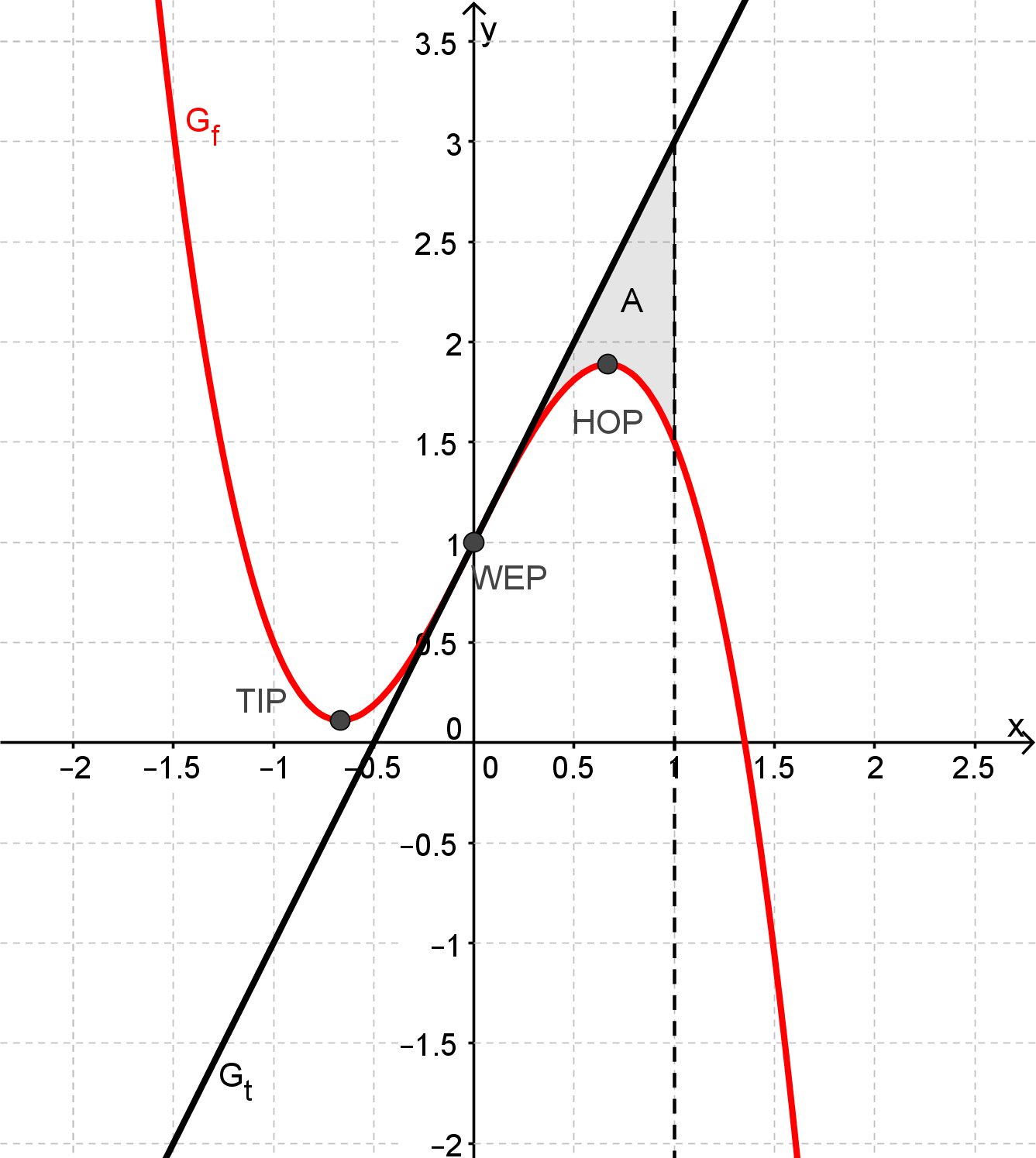
Der Graph , die Tangente und die Gerade mit der Gleichung schließen im I. Quadrant des Koordinatensystems ein endliches Flächenstück ein. Kennzeichnen Sie dieses Flächenstück in Ihrer Zeichnung aus Aufgabe 1.3 und berechnen Sie die Maßzahl seines Flächeninhalts. (5 BE)