Teil 2, Analysis I
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellungen als PDF zum Ausdrucken findest du hier.
- 1
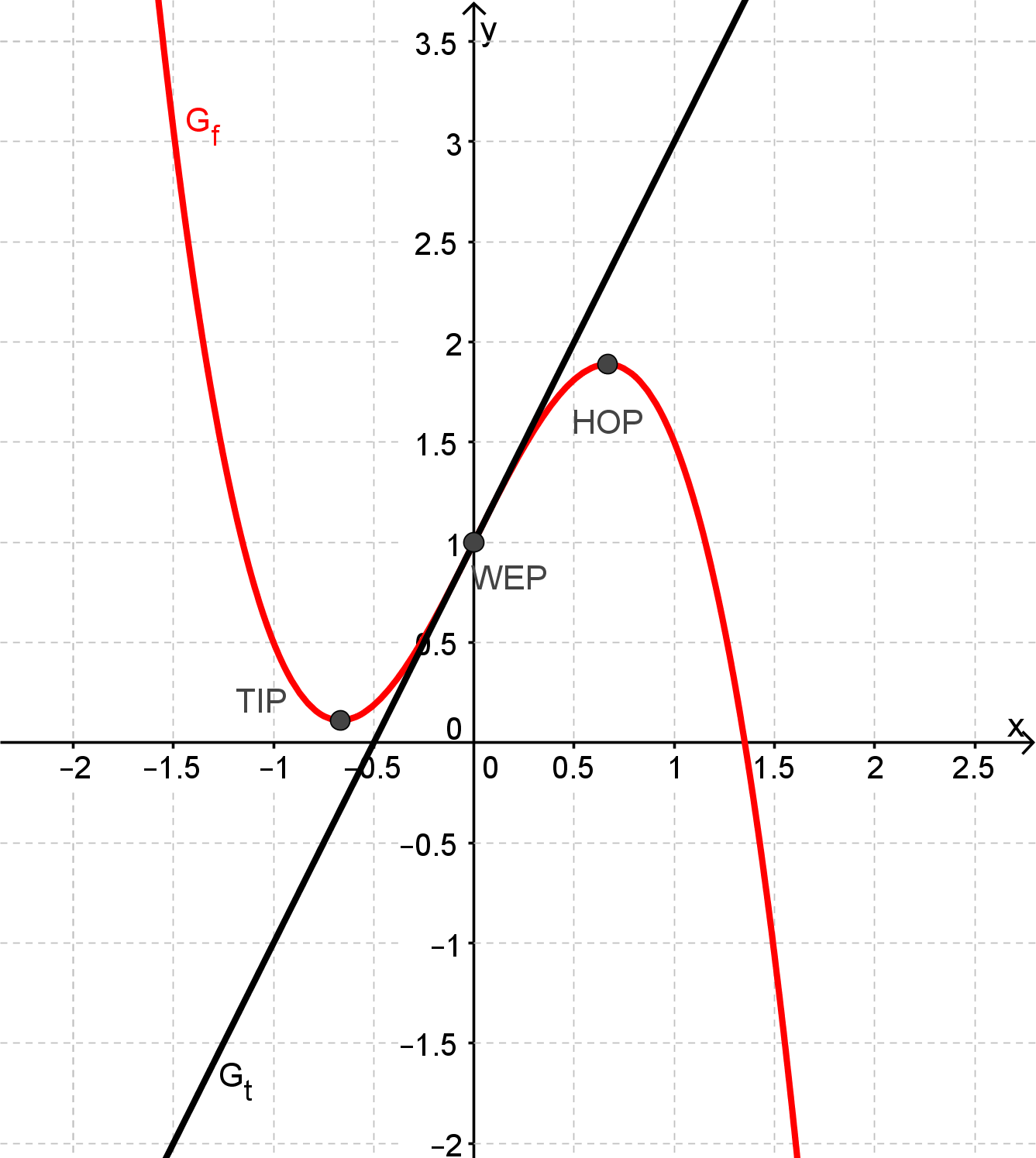
Der Graph einer auf definierten ganzrationalen Funktion f vom Grad drei verläuft durch den Punkt und besitzt im Schnittpunkt mit der y-Achse einen Wendepunkt. Für die Wendetangente gilt: mit der Definitionsmenge .
Stellen Sie eine Funktionsgleichung von f auf.
(Mögliches Teilergebnis: ) (6 BE)
Bestimmen Sie jeweils Art und Koordinaten der relativen Extrempunkte von und begründen Sie, warum f nur eine einfache Nullstelle besitzt. (8 BE)
Zeichnen Sie unter Verwendung aller bisherigen Ergebnisse den Graphen und die Tangente im Bereich in ein kartesisches Koordinatensystem.
Maßstab für beide Achsen: (5 BE)
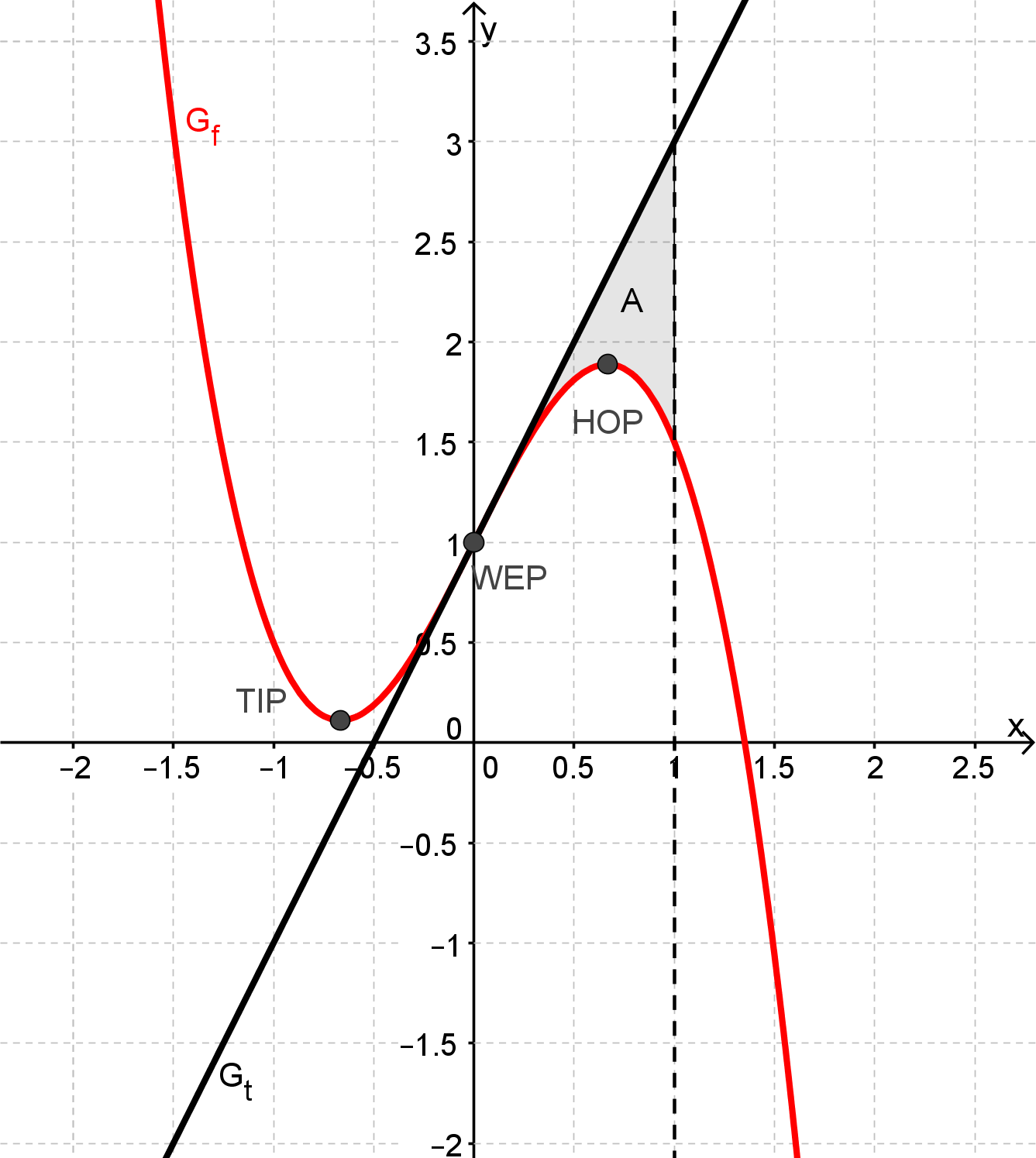
Der Graph , die Tangente und die Gerade mit der Gleichung schließen im I. Quadrant des Koordinatensystems ein endliches Flächenstück ein. Kennzeichnen Sie dieses Flächenstück in Ihrer Zeichnung aus Aufgabe 1.3 und berechnen Sie die Maßzahl seines Flächeninhalts. (5 BE)
- 2
Der zeitliche Verlauf der Temperatur eines in einer großen Tasse eingeschenkten Frühstückstees wird in einem Schülerexperiment untersucht. Als Grundlage wird näherungsweise die Modellfunktion T mit der Funktionsgleichung mit und verwendet. Dabei steht die Variable t für die Beobachtungszeit t in Minuten ab dem Beginn des Experiments, welches mit dem Eingießen des Tees in die Tasse zum Zeitpunkt startet. Der jeweilige Funktionswert von T gibt die Temperatur des Tees in zum Zeitpunkt t an. Der Tee in der Tasse hat zu Beginn des Experminents um 8:55 Uhr eine Temperatur von . Um 9:15 Uhr beträgt die Temperatur nur noch .
Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.
Bestimmen Sie die Werte der Parameter a und b. Runden Sie gegebenenfalls auf eine Nachkommastelle. Erläutern Sie, welche Bedeutung der Wert 22 im Funktionsterm der Funktion T für die Funktionswerte der Modellfunktion hat und bringen Sie diesen Wert in Zusammenhang mit dem durchgeführten Experiment. (5 BE)
Für die folgende Teilaufgabe gilt ;
Als angenehm wird eine Trinktemperatur von empfunden. Berechnen Sie, um welche Uhrzeit diese Temperatur erreicht wird. Runden Sie die Zeitangabe auf ganze Minuten. (3 BE)
- 3
Ein Tipi Zelt in einem Skigebiet hat die Form eines geraden Kreiskegels, dessen Mantellinie die Länge hat (siehe Zeichnung). Das Zelt besitzt ein Innenvolumen, das bei gleichbleibender Länge der Mantellinie von der Höhe h des Zeltes abhängt. Der jeweilige Funktionswert der Funktion beschreibt dieses Innenraumvolumen.
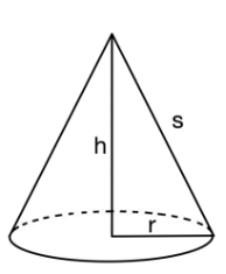
Aus optischen Gründen soll dabei die Höhe h des Tipi Zeltes mindestens 4m und maximal 6m betragen. Dabei steht h für die Höhe des Zelts in m und V(h) für das Volumen des Zelts in .
Bei den Berechnungen kann auf das Mitführen von Einheiten verzichtet werden.
Stellen Sie eine Gleichung der Funktion V auf.
(Mögliches Teilergebnis: ) (3 BE)
Bestimmen Sie unter den oben genannten Vorgaben, für welche Höhe h das Tipi Zelt den maximalen Rauminhalt aufweist. Berechnen Sie für diesen Fall den Durchmesser des Bodens des Tipi Zeltes. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen. (8 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?