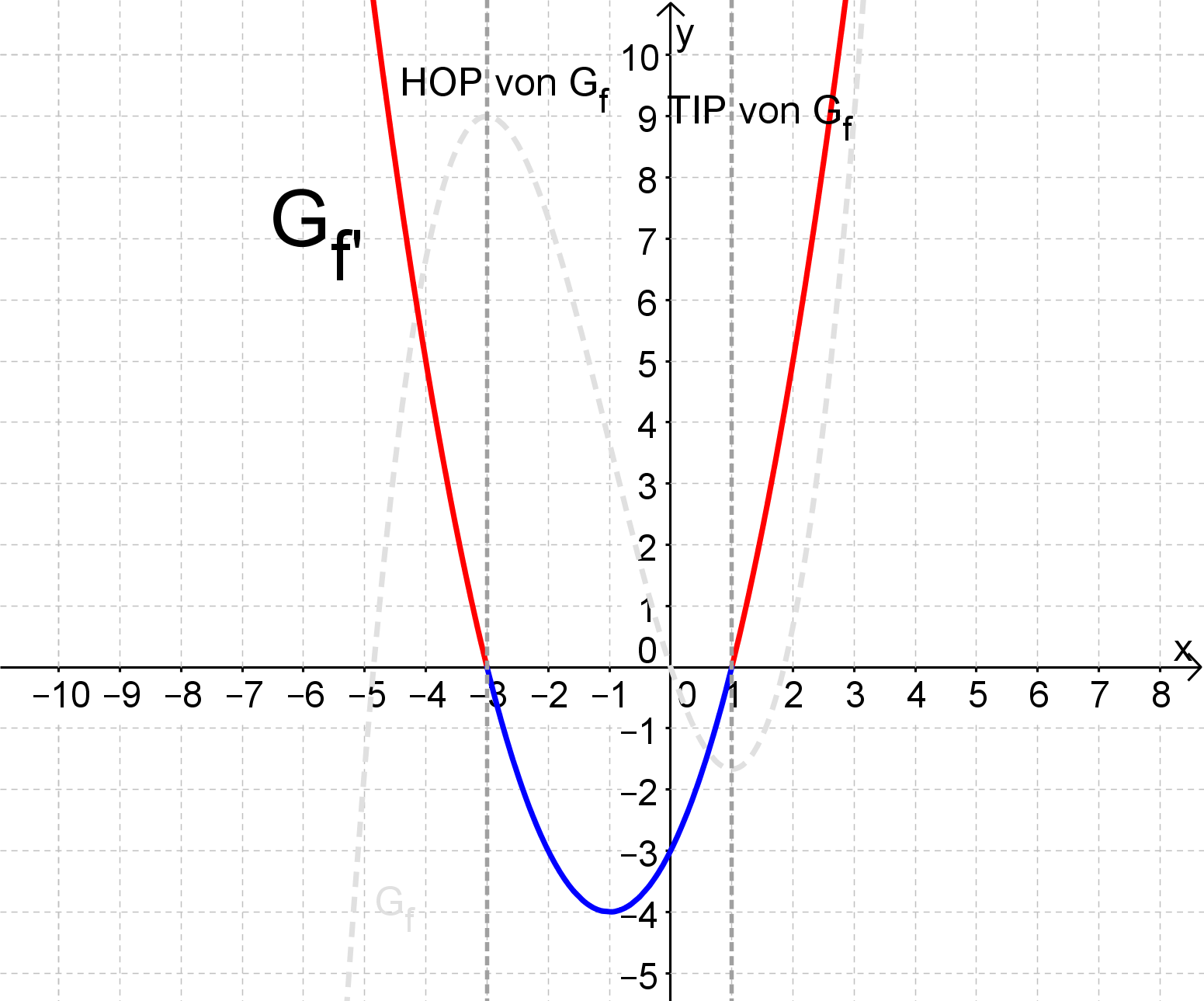
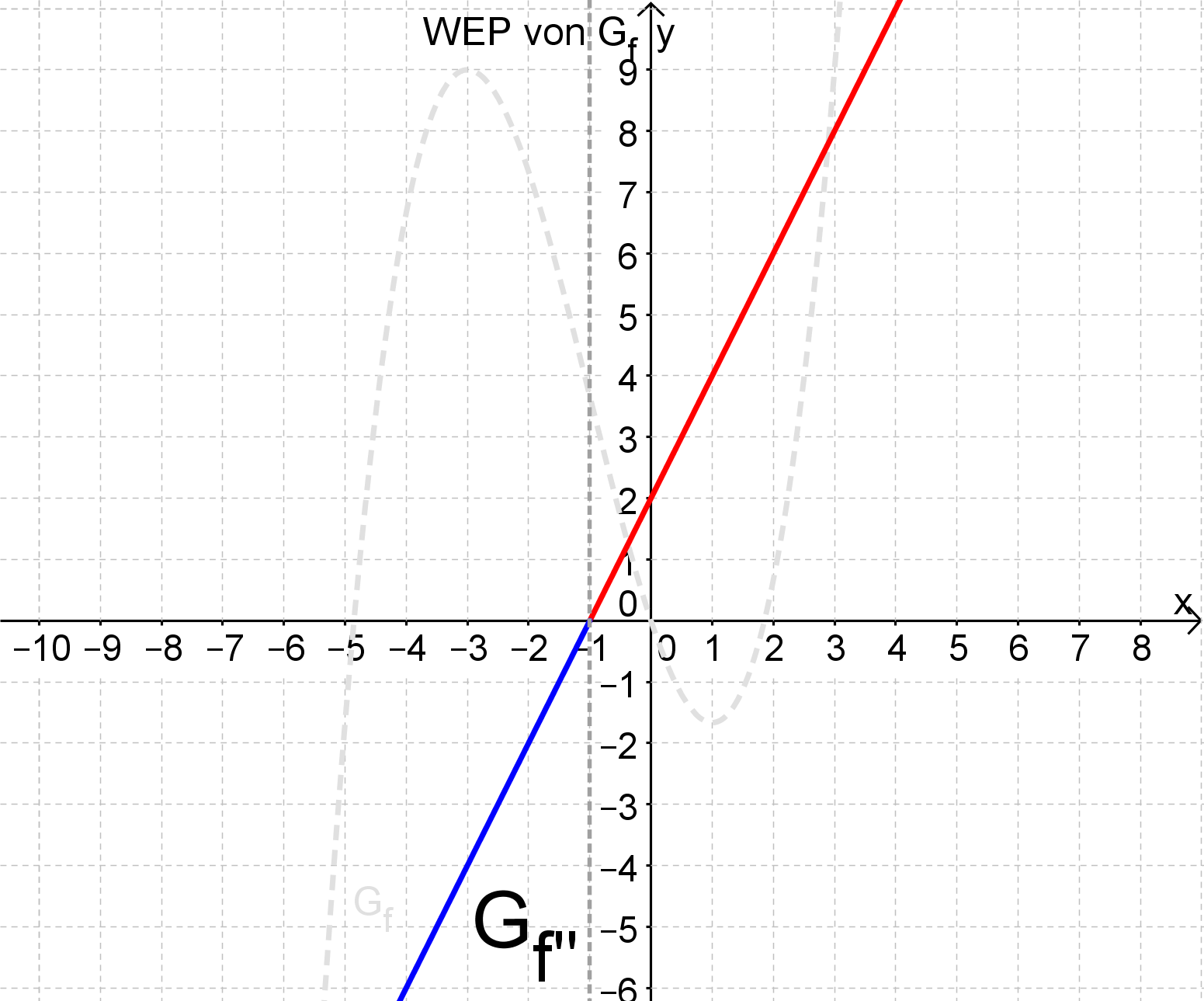
Um das Monotonieverhalten (steigend/fallend) und das Krümmungsverhalten (links- oder rechtsgekrümmt) zu untersuchen, kannst du ähnliche Methoden verwenden.
In dieser Aufgabe sollst du dir Gedanken über die Gemeinsamkeiten und Unterschiede machen.
Egal, ob du später eine Skizze oder eine Tabelle anfertigen wirst (oder sogar mit einer höheren Ableitung arbeiten wirst), zunächst musst du Vorarbeit leisten.
Vergleiche, wie du die Kandidaten für Extrem- und Wendestellen bekommst.
Du untersuchst das Monotonie- und Krümmungsverhalten mithilfe einer Skizze. Wodurch unterscheiden sich die Skizzen zur Monotonie und zur Krümmung?
Statt mit einer Skizze kannst du das Monotonie- und Krümmungsverhalten auch mithilfe von Tabellen untersuchen. Wodurch unterscheiden sich die Monotonietabelle und die Krümmungstabelle voneinander?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?