Visuelle Aufgaben zu Kreisumfang und Kreisfläche

1
Berechne die Länge der Linien.
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Du siehst einen Dreiviertelkreis. Die Länge der Linie ist demnach ein Dreiviertel eines Kreisumfangs. Der Durchmesser des Dreiviertelkreises beträgt $12 cm$ . Sein Radius ist also $r = 6 cm$ . Den Umfang eines Kreises berechnest du mit:
  $U = 2 \cdot π \cdot r$
  Für einen Dreiviertelkreis erhältst du demnach:
  $U_{\frac{3}{4}}$ $=$ $\frac{3}{4} (2 \cdot π \cdot r)$
  ↓
  Klammer auflösen und kürzen
  $=$ $\frac{3}{2} \cdot π \cdot r$
  ↓
  $π \approx 3,14$
  $\approx$ $1,5 \cdot 3,14 \cdot 6 cm$
  $=$ $28,26 cm$
  Antwort: Die Linie hat eine Länge von etwa $28,26 cm$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege dir, welcher Teil eines ganzen Kreises dargestellt ist.
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Die Linie setzt sich aus zwei Halbkreisen mit dem gleichen Radius $r = 4 cm$ zusammen. Somit erhältst du einen ganzen Kreis und kannst den Umfang dieses Kreises berechnen.
  $U$ $=$ $2 \cdot π \cdot r$
  $=$ $2 \cdot π \cdot 4 cm$
  $=$ $8 cm \cdot π$
  ↓
  $π \approx 3,14$
  $\approx$ $8 cm \cdot 3,14$
  $=$ $25,12 cm$
  Antwort: Die Linie hat eine Länge von etwa $25,12 cm$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege dir, aus welchen Teilen eines Kreises die Linie besteht.
3. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Die Linie setzt sich aus drei Halbkreisen zusammen. Der $orange$ Halbkreis hat einen Radius von $r=2 cm$ .
  Der $rote$ Halbkreis hat einen Radius von $r=4 cm$ und der $türkisfarbige$ Halbkreis hat einen Radius von $r=6 cm$ .
  Den Kreisumfang berechnest du mit : $U = 2 \cdot π \cdot r$
  Berechne nun für jeden Halbkreis den halben Umfang mit: $U = π \cdot r$
  $U_{1}$ $=$ $π \cdot r$
  $=$ $π \cdot 2 cm$
  $U_{2}$ $=$ $π \cdot r$
  $=$ $π \cdot 4 cm$
  $U_{3}$ $=$ $π \cdot r$
  $=$ $π \cdot 6 cm$
  Berechne nun die Summe aus den drei halben Kreisumfängen:
  $U$ $=$ $U_{1} + U_{2} + U_{3}$
  $=$ $π \cdot 2 cm + π \cdot 4 cm + π \cdot 6 cm$
  $=$ $π \cdot 12 cm$
  ↓
  $π \approx 3,14$
  $\approx$ $3,14 \cdot 12 cm$
  $=$ $37,68 cm$
  Antwort: Die Linie hat eine Länge von etwa $37,68 cm$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Überlege dir, aus welchen Teilen eines Kreises die Linie besteht.
2
Berechne den Gesamtumfang der Figur. Die Maße kannst du dem Bild unten entnehmen. Runde dein Ergebnis auf eine Nachkommastelle.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreis
Die allgemeine Formel zur Berechnung des Kreisumfangs ist:
$U_{Kreis} = 2 π \cdot r$
Die Figur setzt sich aus dem blauen Kreis und dem weißen Halbkreis zusammen. Daraus folgt für den Gesamtumfang:
$\begin{array}{rcl} U_{gesamt} & = & U_{weiß} + U_{blau} \\ U_{gesamt} & = & [\frac{1}{2} (2 π \cdot r) + d] + 2 π \cdot r \end{array}$
Vergiss nicht den Durchmesser zum Halbkreis hinzu zu addieren für die untere Linie, des Halbkreises.
Der Durchmesser $d$ der beiden Kreise ist in der Zeichnung gegeben. Für die Formel brauchst du aber den Radius $r$ . Diesen kannst du wie folgt berechnen:
$\begin{array}{rcl} d = 2 \cdot r \Rightarrow r & = & \frac{1}{2} d \\ r & = & \frac{1}{2} \cdot 15 cm = 7,5 cm \end{array}$
Nun brauchst du nur noch die gegebenen Werte einzusetzen.
$\begin{array}{rcl} U_{gesamt} & = & [\frac{1}{2} (2 π \cdot r) + d] + 2 π \cdot r \\ U_{gesamt} & = & [\frac{1}{2} (2 π \cdot 7,5 cm) + 15 cm] + 2 π \cdot 7,5 cm \\ U_{gesamt} & \approx & 85,7 cm \end{array}$
Das heißt, dass der Gesamtumfang ca. 85,7 cm beträgt.
3
Berechne den Gesamtumfang der unten dargestellten Figur.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreisumfang
Die Figur setzt sich aus mehreren Figuren zusammen.
Sie besteht aus dem hier grünen Kreis, dem blauen Halbkreis und den beiden orangen Halbkreisen. Der Umfang der Figur setzt sich aus den Umfängen der bunten Kreisteile zusammen.
Die allgemeine Formel zur Berechnung des Kreisumfangs ist:
$U = 2 π \cdot r$
Berechne nun die Umfänge $U_{grün}$ , $U_{blau}$ und $U_{orange}$ .
$U_{grün}$ ist der Umfang eines Kreises mit einem Radius von $1,5 cm$ .
$\begin{array}{l} U_{grün} = 2 π \cdot 1,5 cm \\ = π \cdot 3 cm \\ \approx 3,14 \cdot 3 cm \\ = 9,42 cm \end{array}$
$U_{blau}$ ist der Umfang eines Halbkreises, von dem die Längen der angrenzenden orangen Schnittlinien abgezogen werden müssen. Der Umfang des blauen Objekts besteht aus dem halben Umfang eines ganzen Kreises und der Länge der unteren Seite minus $2 \cdot 1 cm = 2 cm$ . Die untere Seite ist $7 cm$ lang. Das ist außerdem auch der Durchmesser des Halbkreises. Somit ist der Radius des Halbkreises $7 cm : 2 = 3,5 cm$ .
$\begin{array}{l} U_{blau} = \frac{1}{2} \cdot 2 π \cdot 3,5 cm + (7 cm - 2 cm) \\ = π \cdot 3,5 cm + (7 cm - 2 cm) \\ \approx 3,14 \cdot 3,5 cm + 5 cm \\ = 10,99 cm + 5 cm \\ = 15,99 cm \end{array}$
$U_{orange}$ sind zwei Halbkreise mit dem gleichen Durchmesser von $1 cm$ . Deren Umfang ist der gleiche wie der eines ganzen Kreises mit Durchmesser $1 cm$ . Der Radius beträgt hier $0,5 cm$ . Die obere Seite der Halbkreise müssen wir nicht berechnen, da sie an den blauen Halbkreis angrenzen.
$\begin{array}{l} U_{orange} = 2 π \cdot 0,5 cm \\ = π \cdot 1 cm \\ \approx 3,14 \cdot 1 cm \\ = 3,14 cm \end{array}$
Der Gesamtumfang setzt sich nun aus der Summe der Umfänge $U_{grün}$ , $U_{blau}$ und $U_{orange}$ zusammen.
$\begin{array}{rcllll} U_{Gesamt} & = & U_{grün} & + U_{blau} & + U_{orange} \\ \approx & 9,42 cm & + 15,99 cm & + 3,14 cm \\ = & 28,55 cm \end{array}$
Der Gesamtumfang der Figur beträgt in etwa $28,55 cm$ .
4
Du siehst eine Abbildung von Pacman. Berechne den Umfang dieser Figur. Ein Kästchen entspricht dabei 0,5cm. Außerdem kannst du annehmen, dass der Mund von Pacman ein Viertel des Kreises ausmacht. Runde das Ergebnis auf 2 Nachkommastellen.
cm

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnung des Umfangs eines Kreises
Den Umfang eines Kreises berechnest du mit der Formel:
$U = 2 \cdot π \cdot r = d \cdot π$
Du kannst den Durchmesser d durch Zählen der Kästchen herausfinden Der Durchmesser ist 10 Kästchen lang, also $d = 0,5 c m \cdot 10 = 5 c m$ .
$U = d \cdot π = 5 c m \cdot π \approx 15,71 c m$
Um nur den Umfang von dem $\frac{3}{4}$ -Kreis zu berechnen, multiplizierst du den Umfang mit $\frac{3}{4}$ :
$U_{k r e i s p a c m a n} = \frac{3}{4} \cdot 5 c m \cdot π = \frac{3}{4} \cdot 15,71 c m \approx 11,78 c m$
Als letzten Schritt darfst du nicht vergessen den Umfang des Mundes zu berechnen. Die obere und untere Linie entsprechen jeweils dem Radius des Kreises, also der Hälfte des Durchmessers:
$r = \frac{5 c m}{2} = 2,5 c m$
Die Länge der beiden Linien rechnest du noch zum vorher berechneten Umfang dazu:
$U_{p a c m a n} = 11,78 c m + 2,5 c m + 2,5 c m = 16,78 c m$
Der Umfang von Pacman beträgt also $16,78 c m$ .
5
Lisa hat ein Pferd, eine Kuh, ein Schaf und einen Esel. Sie möchte jedem ein eigenes Stück Wiese zur Verfügung stellen. Dafür wird ein Zaun, um die Felder herum benötigt. Berechne wie viel Zaun Lisa braucht. Ein Kästchen in der Abbildung entspricht 10m in der Realität. Runde dein Ergebnis auf 2 Nachkommastellen.
Fällt dir ein einfacher und schneller Lösungsweg auf?
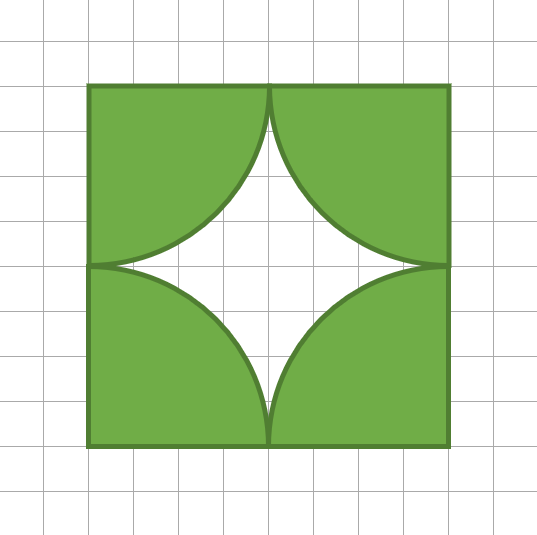m

Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnung des Umfangs eines Kreises
Den Umfang eines Kreises berechnest du mit der Formel:
$U = 2 \cdot π \cdot r = d \cdot π $
Der Radius des Kreises ist 4 Kästchen lang. Das entspricht 40m. Nun kannst du den Wert in die Formel einsetzen:
$U_{K r e i s} = 2 \cdot π \cdot r = 2 \cdot π \cdot 40 m = 80 m \cdot π \approx 251,33 m$
Das ist die Länge der 4 Kreisbögen. Nun musst du noch die Länge des Zauns um die 4 Felder herum berechnen. Du hast 4 gleich lange Seiten von je 8 Kästchen, also 80m:
$U_{a u ß e n} = 4 \cdot 80 m = 320 m$
Der Gesamtumfang ist die Summe aus dem Umfang der Kreisbögen und dem Umfang um die Felder herum.
$U_{g e s a m t} = U_{K r e i s} + U_{a u ß e n} = 251,33 m + 320 m = 571,33 m$
Lisa braucht also einen Zaun mit einer Länge von 571,33m.
Da du 4 gleiche Viertelkreise hast, kannst du diese zu einem vollständigen Kreis ergänzen. Deshalb kannst du in der Aufgabe gleich den Umfang eines ganzen Kreises berechnen.
6
Berechne bei den einzelnen Figuren jeweils den Umfang und den Flächeninhalt.
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Berechnung des Umfangs
  Der Umfang der Figur $U_{F}$ setzt sich aus zwei geraden $6 cm$ langen Strecken und einem Viertel Kreisumfang zusammen.
  Die Formel für den Kreisumfang lautet: $U = 2 π r$
  Ein Viertel des Kreisumfangs kann dann mit $U_{\frac{1}{4}} = \frac{1}{4} \cdot (2 π r) = 0,5 π r$ berechnet werden. Der Kreisradius $r$ beträgt bei dieser Figur $6 cm$ , so
  dass du für $U_{\frac{1}{4}}$ folgenden Wert erhältst:
  $U_{\frac{1}{4}}$ $=$ $0,5 \cdot π \cdot r$
  ↓
  $π \approx 3,14$
  $\approx$ $0,5 \cdot 3,14 \cdot 6 cm$
  $=$ $9,42 cm$
  Damit kannst du den gesamten Umfang der Figur berechnen:
  $U_{F}$ $=$ $2 \cdot Radius + U_{\frac{1}{4}}$
  $=$ $2 \cdot 6 cm + 9,42 cm$
  $=$ $21,42 cm$
  Antwort: Die Figur hat einen Umfang von etwa $21,42 cm$ .
  Berechnung des Flächeninhaltes
  Die Kreisfläche berechnest du mit der Formel $A = π r^{2}$ .
  Die abgebildete Figur ist ein Viertel eines Kreises mit dem Radius $r = 6 cm$ . Den Flächeninhalt $A_{F}$ dieser Figur kannst du demnach mit $A_{F} = \frac{1}{4} \cdot π \cdot r^{2}$ berechnen:
  $A_{F}$ $=$ $= \frac{1}{4} \cdot π \cdot r^{2}$
  ↓
  $π \approx 3,14$
  $\approx$ $\frac{1}{4} \cdot 3,14 \cdot (6 cm)^{2}$
  $=$ $28,26 {cm}^{2}$
  Antwort: Die Figur hat einen Flächeninhalt von etwa $28,26 {cm}^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte bei der Berechnung des Umfangs, aus welchen Teilen er sich zusammensetzt. Bei der Berechnung des Flächeninhaltes suche nach bekannten geometrischen Figuren.
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Berechnung des Umfangs
  Der Umfang der Figur $U_{F}$ setzt sich aus vier Vierteln eines Kreisumfangs zusammen. Somit ist der Umfang $U_{F}$ genau der Umfang eines Kreises mit dem Radius $r = 6 cm$ .
  Die Formel für den Kreisumfang lautet: $U = 2 π r$
  Für den Umfang der Figur $U_{F}$ gilt:
  $U_{F}$ $=$ $2 \cdot π \cdot r$
  ↓
  $π \approx 3,14$
  $\approx$ $2 \cdot 3,14 \cdot 6 cm$
  $=$ $37,68 cm$
  Antwort: Die Figur hat einen Umfang von etwa $37,68 cm$ .
  Berechnung des Flächeninhaltes
  Für die Berechnung des Flächeninhaltes $A_{F}$ denke dir ein Quadrat mit der Seitenlänge $12 cm$ um die Figur gezeichnet. So wie in der folgenden Abbildung.
  Die Quadratfläche $A_{Q}$ besteht aus vier $V i e r t e l k r e i s f l ä c h e n$ und der Fläche der Figur $A_{F}$ . Die vier $V i e r t e l k r e i s f l ä c h e n$ lassen sich zu einer ganzen Kreisfläche $A_{K}$ zusammensetzen, die du mit der Formel $A_{K} = π r^{2}$ berechnen kannst. Dabei beträgt der Radius $r = 6 cm$ . Somit erhältst du den Flächeninhalt $A_{F}$ der Figur als Differenz der Quadratfläche $A_{Q}$ und der Kreisfläche $A_{K}$ : $A_{F} = A_{Q} - A_{K}$
  $A_{F}$ $=$ $(12 cm)^{2} - π \cdot r^{2}$
  ↓
  $π \approx 3,14$
  $\approx$ $144 {cm}^{2} - 3,14 \cdot (6 cm)^{2}$
  $=$ $144 {cm}^{2} - 113,04 {cm}^{2}$
  $=$ $30,96 {cm}^{2}$
  Antwort: Die Figur hat einen Flächeninhalt von etwa $30,96 {cm}^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte bei der Berechnung des Umfangs, aus welchen Teilen er sich zusammensetzt. Bei der Berechnung des Flächeninhaltes suche nach bekannten geometrischen Figuren.
3. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Berechnung des Umfangs
  Der Umfang der Figur $U_{F}$ setzt sich aus zwei geraden $16 cm$ langen Strecken und zwei Hälften eines Kreisumfangs zusammen. Das ist genau der Umfang eines Kreises mit dem Radius $r = 3 cm$ . Die Formel für den Kreisumfang lautet:
  $U = 2 π r$
  Für den Umfang der Figur $U_{F}$ gilt:
  $U_{F}$ $=$ $2 \cdot 16 cm + 2 \cdot π \cdot 3 cm$
  ↓
  $π \approx 3,14$
  $\approx$ $2 \cdot 16 cm + 2 \cdot 3,14 \cdot 3 cm$
  $=$ $50,84 cm$
  Antwort: Die Figur hat einen Umfang von etwa $50,84 cm$ .
  Berechnung des Flächeninhaltes
  Die Figur setzt sich aus zwei Teilen zusammen, einem Kreis mit dem Radius $r = 3 cm$ (zwei Halbkreise ergeben einen ganzen Kreis) und einem Rechteck mit den Seitenlängen $a = 16 cm$ und $b = 6 cm$ . Den Flächeninhalt $A_{F}$ dieser Figur berechnest du als Summe einer Kreisfläche und einer Rechteckfläche mit:
  $\begin{aligned} A_{F} = & π \cdot r^{2} + a \cdot b \\ = & π \cdot (3 cm)^{2} + 16 cm \cdot 6 cm \\ \approx & 3,14 \cdot 9 {cm}^{2} + 96 {cm}^{2} \\ = & 124,26 {cm}^{2} \end{aligned}$
  Antwort: Die Figur hat einen Flächeninhalt von etwa $124,26 {cm}^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte bei der Berechnung des Umfangs, aus welchen Teilen er sich zusammensetzt. Bei der Berechnung des Flächeninhaltes suche nach bekannten geometrischen Figuren.
4. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Berechnung des Umfangs
  Der Umfang der Figur $U_{F}$ ist die Summe aus zwei Kreisumfängen. Der eine Kreis hat einen Radius von $r_{1} = 6 cm$ und der andere Kreis hat einen Radius von $r_{2} = 2 cm$ . Die Formel für den Kreisumfang lautet:
  $U = 2 π r$
  Für den Umfang der Figur $U_{F}$ ergibt sich somit:
  $U_{F}$ $=$ $U_{g r o ß e r K r e i s} + U_{k l e i n e r K r e i s}$
  $=$ $2 \cdot π \cdot 6 cm + 2 \cdot π \cdot 2 cm$
  ↓
  $π$ $\approx$ 3,14
  $\approx$ $2 \cdot 3,14 \cdot 6 cm + 2 \cdot 3,14 \cdot 2 cm$
  $=$ $37,68 cm + 12,56 cm$
  $=$ $50,24 cm$
  Antwort: Die Figur hat einen Umfang von etwa $50,24 cm$ .
  Berechnung des Flächeninhaltes
  Den Flächeninhalt $A_{F}$ dieser Figur berechnest du als Differenz von zwei Kreisflächen. $A_{F} = A_{g r o ß e r K r e i s} - A_{k l e i n e r K r e i s}$
  $\begin{aligned} A_{F} = & π \cdot {r_{1}}^{2} - π \cdot {r_{2}}^{2} \\ = & π \cdot (6 cm)^{2} - π \cdot (2 cm)^{2} \\ \approx & 3,14 \cdot 36 {cm}^{2} - 3,14 \cdot 4 {cm}^{2} \\ = & 100,48 {cm}^{2} \end{aligned}$
  Antwort: Die Figur hat einen Flächeninhalt von etwa $100,48 {cm}^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte: Bei dieser Figur geht es nur um den gefärbten Bereich.
5. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Berechnung des Umfangs
  Der Umfang der Figur $U_{F}$ ist die Summe aus vier halben Kreisumfängen, das heißt aus insgesamt zwei Kreisumfängen. Der Kreis hat einen Radius von $r = 4 cm$ . Die Formel für den Kreisumfang lautet:
  $U_{K} = 2 π r$
  Für den Umfang der Figur $U_{F}$ ergibt sich somit:
  $U_{F}$ $=$ $2 \cdot U_{K}$
  $=$ $2 \cdot (2 \cdot π \cdot 4 cm)$
  ↓
  $π$ $\approx$ 3,14
  $\approx$ $4 \cdot 3,14 \cdot 4 cm$
  $=$ $50,24 cm$
  Antwort: Die Figur hat einen Umfang von etwa $50,24 cm$ .
  Berechnung des Flächeninhaltes
  Damit es deutlich wird, kannst du dir die Mitte der Figur ohne Farbe vorstellen. Du siehst hier nun ein Quadrat mit der Seitenlänge $a = 8 cm$ . Die vier Halbkreise ergeben zwei ganze Kreise. Den Flächeninhalt $A_{F}$ dieser Figur berechnest du als Summe zweier $K r e i s f l ä c h e n$ und einer Quadratfläche mit: $A_{F} = 2 \cdot A_{F} + A_{Q}$
  $\begin{aligned} A_{F} = & 2 \cdot (π \cdot r^{2}) + a^{2} \\ = & 2 \cdot π \cdot (4 cm)^{2} + (8 cm)^{2} \\ \approx & 2 \cdot 3,14 \cdot 16 {cm}^{2} + 64 {cm}^{2} \\ = & 164,48 {cm}^{2} \end{aligned}$
  Antwort: Die Figur hat einen Flächeninhalt von etwa $164,48 {cm}^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte bei der Berechnung des Umfangs, aus welchen Teilen er sich zusammensetzt. Bei der Berechnung des Flächeninhaltes suche nach bekannten geometrischen Figuren.
6. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Berechnung des Umfangs
  Der Umfang $U_{F}$ der Figur besteht aus einem $orangefarbigen$ großen Halbkreis mit dem Radius $r_{1} = 5 cm$ und zwei kleinen $lilafarbigen$ Halbkreisen mit gleichem Radius $r_{2} = 2,5 cm$ . Die zwei $lilafarbigen$ Halbkreise kannst du zu einem ganzen Kreis zusammensetzen. Für den Umfang $U_{F}$ der Figur gilt demnach:
  $U_{F}$ $=$ $\frac{1}{2} \cdot U + U$
  $=$ $\frac{1}{2} \cdot (2 \cdot π \cdot r_{1}) + 2 \cdot π \cdot r_{2}$
  $=$ $\frac{1}{2} \cdot (2 \cdot π \cdot 5 cm) + 2 \cdot π \cdot 2,5 cm$
  $=$ $π \cdot 5 cm + π \cdot 5 cm$
  $=$ $10 \cdot π cm$
  ↓
  $π \approx 3,14$
  $\approx$ $10 \cdot 3,14 cm$
  $=$ $31,4 cm$
  Antwort: Die Figur hat einen Umfang von etwa $31,4 cm$ .
  Berechnung des Flächeninhaltes
  Die Figur kannst du geschickt zerlegen und wieder zusammensetzen. Wie es geht zeigt das nächste Bild.
  Denke dir den Durchmesser im großen Halbkreis eingezeichnet. Längs dieser Linie kannst du den $lilafarbigen$ Halbkreis abschneiden und in den unteren kleinen Halbkreis einfügen. Der Flächeninhalt $A_{F}$ der Figur ist nun genau der Flächeninhalt des großen Halbkreises.
  Für diesen Flächeninhalt gilt:
  $A_{F}$ $=$ $\frac{1}{2} \cdot A_{K}$
  $=$ $\frac{1}{2} \cdot π \cdot r_{1}^{2}$
  $=$ $\frac{1}{2} \cdot π \cdot (5 cm)^{2}$
  $=$ $\frac{1}{2} \cdot π \cdot 25 {cm}^{2}$
  $=$ $12,5 \cdot π {cm}^{2}$
  ↓
  $π \approx 3,14$
  $\approx$ $12,5 \cdot 3,14 {cm}^{2}$
  $=$ $39,25 {cm}^{2}$
  Antwort: Die Figur hat einen Flächeninhalt von etwa $39,25 {cm}^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte bei der Berechnung des Umfangs, aus welchen Teilen er sich zusammensetzt. Bei der Berechnung des Flächeninhaltes nutze die Strategie "Zerlegen" und "Ergänzen"
7. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Berechnung des Umfangs
  Der Umfang $U_{F}$ der Figur besteht aus zwei $grünen Halbkreisen$ mit dem Radius $r = 2 cm$ und zwei $lilafarbigen Strecken$ der Länge $b = 10 cm$ . Die zwei $grünen Halbkreise$ kannst du zu einem ganzen Kreis zusammensetzen.
  Für den Umfang $U_{F}$ der Figur gilt demnach:
  $U_{F}$ $=$ $U_{K} + 2 \cdot b$
  $=$ $2 \cdot π \cdot r + 2 \cdot b$
  $=$ $2 \cdot π \cdot 2 cm + 2 \cdot 10 cm$
  $=$ $4 \cdot π cm + 20 cm$
  ↓
  $π \approx 3,14$
  $\approx$ $4 \cdot 3,14 cm + 20 cm$
  $=$ $12,56 cm + 20 cm$
  $=$ $32,56 cm$
  Berechnung des Flächeninhaltes
  Bei der Berechnung des Flächeninhaltes kannst du die Strategie "Zerlegen" und "Ergänzen" anwenden. Denke dir den linken $lilafarbigen$ Halbkreis abgeschnitten und auf der rechten Seite wieder eingefügt. Der Flächeninhalt $A_{F}$ der Figur ist nun genau der Flächeninhalt eines Rechtecks mit den Seitenlängen $a = 12 cm - 2 cm = 10 cm$
  und $b = 4 cm$ .
  Für den Flächeninhalt $A_{F}$ der Figur gilt demnach:
  $A_{F}$ $=$ $a \cdot b$
  $=$ $10 cm \cdot 4 cm$
  $=$ $40 {cm}^{2}$
  Antwort: Die Figur hat einen Flächeninhalt von $40 {cm}^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte bei der Berechnung des Umfangs, aus welchen Teilen er sich zusammensetzt. Bei der Berechnung des Flächeninhaltes suche nach bekannten geometrischen Figuren.
8. Für diese Aufgabe benötigst Du folgendes Grundwissen: Berechnungen am Kreis
  Berechnung des Umfangs
  Zur Verdeutlichung sind in der obigen Abbildung alle Strecken und Halbkreise farbig gekennzeichnet. Der Umfang der Figur $U_{F}$ setzt sich aus $5 roten$ waagrechten Teilstrecken und $6 roten$ senkrechten Strecken sowie $5 g r \ddot{u} n e n$ halben Kreisumfängen zusammen. Den Kreisumfang berechnest du mit: $U_{K} = 2 \cdot π \cdot r$
  $5 rote$ waagrechte Teilstrecken: $b = (1 + 2 + 4 + 2 + 1) cm = 10 cm$
  $6 rote$ senkrechte Strecken: $h = (1 + 1 + 2 + 2 + 1 + 1) cm = 8 cm$
  $2 kleine grüne$ Halbkreise (Nr. 1 und 5) ergeben einen ganzen Kreis mit dem Radius $r = 0,5 cm \Rightarrow$
  $U_{1} = 2 \cdot π \cdot 0,5 cm = π cm$
  $2 mittlere grüne$ Halbkreise (Nr. 2 und 4) ergeben einen ganzen Kreis mit dem Radius $r = 1 cm \Rightarrow$
  $U_{2} = 2 \cdot π \cdot 1 cm = 2 π cm$
  $1 großer grüner$ Halbkreis (Nr. 3) mit dem Radius $r = 2 cm \Rightarrow$
  $U_{3} = \frac{1}{2} (2 \cdot π \cdot 2 cm) = 2 π cm$
  Damit erhältst du für den gesamten Umfang der Figur:
  $U_{F}$ $=$ $b + h + U_{1} + U_{2} + U_{3}$
  $=$ $10 cm + 8 cm + (π + 2 π + 2 π) cm$
  $=$ $18 cm + 5 π cm$
  ↓
  $π \approx 3,14$
  $\approx$ $18 cm + 5 \cdot 3,14 cm$
  $=$ $33,7 cm$
  Antwort: Die Figur hat einen Umfang von etwa $33,7 cm$ .
  Berechnung des Flächeninhaltes
  Zur Verdeutlichung sind in der obigen Abbildung die 5 Quadrate nicht mehr farbig gekennzeichnet. Der Flächeninhalt der Figur setzt sich aus der Fläche der 5 weißen Quadrate und der Fläche von $5 grünen$ Halbkreisen zusammen. Bei den Quadraten sind jeweils 2 gleich groß. Je 2 Halbkreise lassen sich zu einem ganzen Kreis ergänzen.
  Den Flächeninhalt eines Quadrates berechnest du mit $A_{Q} = a^{2}$ . Berechne nun den Flächeninhalt der 5 weißen Quadrate:
  $A_{Q}$ $=$ $A_{1} + A_{2} + A_{3} + A_{4} + A_{5}$
  ↓
  $A_{1} = A_{5}$ und $A_{2} = A_{4}$
  $=$ $2 \cdot (1 cm)^{2} + 2 \cdot (2 cm)^{2} + (4 cm)^{2}$
  $=$ $(2 + 8 + 16) {cm}^{2}$
  $=$ $26 {cm}^{2}$
  Den Flächeninhalt eines Kreises kannst du mit $A_{K} = π \cdot r^{2}$ berechnen. Berechne nun den Flächeninhalt der $5 grünen$ Halbkreise:
  $2 kleine grüne$ Halbkreise (Nr. 1 und 5) ergeben einen ganzen Kreis mit dem Radius $r = 0,5 cm \Rightarrow$
  $A_{K 1} = π \cdot (0,5 cm)^{2} = 0,25 π {cm}^{2}$
  $2 mittlere grüne$ Halbkreise (Nr. 2 und 4) ergeben einen ganzen Kreis mit dem Radius $r = 1 cm \Rightarrow$
  $A_{K 2} = π \cdot (1 cm)^{2} = π {cm}^{2}$
  $1 großer grüner$ Halbkreis (Nr. 3) mit dem Radius $r = 2 cm \Rightarrow$
  $A_{K 3} = \frac{1}{2} (π \cdot (2 cm)^{2}) = 2 π {cm}^{2}$
  $A_{K}$ $=$ $A_{K 1} + A_{K 2} + A_{K 3}$
  $=$ $(0,25 π + π + 2 π) {cm}^{2}$
  $=$ $3,25 π {cm}^{2}$
  ↓
  $π \approx 3,14$
  $\approx$ $3,25 \cdot 3,14 {cm}^{2}$
  $=$ $10,205 {cm}^{2}$
  $\approx$ $10,21 {cm}^{2}$
  Damit erhältst du für den gesamten Flächeninhalt der Figur:
  $A_{F}$ $=$ $A_{Q} + A_{K}$
  $=$ $26 {cm}^{2} + 10,21 {cm}^{2}$
  $=$ $36,21 {cm}^{2}$
  Antwort: Die Figur hat einen Flächeninhalt von etwa $36,21 {cm}^{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Beachte bei der Berechnung des Umfangs, aus welchen Teilen er sich zusammensetzt. Bei der Berechnung des Flächeninhaltes suche nach bekannten geometrischen Figuren.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$U_{\frac{3}{4}}$	$=$	$\frac{3}{4} (2 \cdot π \cdot r)$
	↓	Klammer auflösen und kürzen
	$=$	$\frac{3}{2} \cdot π \cdot r$
	↓	$π \approx 3,14$
	$\approx$	$1,5 \cdot 3,14 \cdot 6 cm$
	$=$	$28,26 cm$

$U$	$=$	$2 \cdot π \cdot r$
	$=$	$2 \cdot π \cdot 4 cm$
	$=$	$8 cm \cdot π$
	↓	$π \approx 3,14$
	$\approx$	$8 cm \cdot 3,14$
	$=$	$25,12 cm$

$U$	$=$	$U_{1} + U_{2} + U_{3}$
	$=$	$π \cdot 2 cm + π \cdot 4 cm + π \cdot 6 cm$
	$=$	$π \cdot 12 cm$
	↓	$π \approx 3,14$
	$\approx$	$3,14 \cdot 12 cm$
	$=$	$37,68 cm$

$U_{\frac{1}{4}}$	$=$	$0,5 \cdot π \cdot r$
	↓	$π \approx 3,14$
	$\approx$	$0,5 \cdot 3,14 \cdot 6 cm$
	$=$	$9,42 cm$

$U_{F}$	$=$	$2 \cdot Radius + U_{\frac{1}{4}}$
	$=$	$2 \cdot 6 cm + 9,42 cm$
	$=$	$21,42 cm$

$A_{F}$	$=$	$= \frac{1}{4} \cdot π \cdot r^{2}$
	↓	$π \approx 3,14$
	$\approx$	$\frac{1}{4} \cdot 3,14 \cdot (6 cm)^{2}$
	$=$	$28,26 {cm}^{2}$

$A_{F}$	$=$	$(12 cm)^{2} - π \cdot r^{2}$
	↓	$π \approx 3,14$
	$\approx$	$144 {cm}^{2} - 3,14 \cdot (6 cm)^{2}$
	$=$	$144 {cm}^{2} - 113,04 {cm}^{2}$
	$=$	$30,96 {cm}^{2}$

$U_{F}$	$=$	$2 \cdot 16 cm + 2 \cdot π \cdot 3 cm$
	↓	$π \approx 3,14$
	$\approx$	$2 \cdot 16 cm + 2 \cdot 3,14 \cdot 3 cm$
	$=$	$50,84 cm$

$U_{F}$	$=$	$U_{g r o ß e r K r e i s} + U_{k l e i n e r K r e i s}$
	$=$	$2 \cdot π \cdot 6 cm + 2 \cdot π \cdot 2 cm$
	↓	$π$ $\approx$ 3,14
	$\approx$	$2 \cdot 3,14 \cdot 6 cm + 2 \cdot 3,14 \cdot 2 cm$
	$=$	$37,68 cm + 12,56 cm$
	$=$	$50,24 cm$

$U_{F}$	$=$	$2 \cdot U_{K}$
	$=$	$2 \cdot (2 \cdot π \cdot 4 cm)$
	↓	$π$ $\approx$ 3,14
	$\approx$	$4 \cdot 3,14 \cdot 4 cm$
	$=$	$50,24 cm$

$A_{Q}$	$=$	$A_{1} + A_{2} + A_{3} + A_{4} + A_{5}$
	↓	$A_{1} = A_{5}$ und $A_{2} = A_{4}$
	$=$	$2 \cdot (1 cm)^{2} + 2 \cdot (2 cm)^{2} + (4 cm)^{2}$
	$=$	$(2 + 8 + 16) {cm}^{2}$
	$=$	$26 {cm}^{2}$

$U_{F}$	$=$	$\frac{1}{2} \cdot U + U$
	$=$	$\frac{1}{2} \cdot (2 \cdot π \cdot r_{1}) + 2 \cdot π \cdot r_{2}$
	$=$	$\frac{1}{2} \cdot (2 \cdot π \cdot 5 cm) + 2 \cdot π \cdot 2,5 cm$
	$=$	$π \cdot 5 cm + π \cdot 5 cm$
	$=$	$10 \cdot π cm$
	↓	$π \approx 3,14$
	$\approx$	$10 \cdot 3,14 cm$
	$=$	$31,4 cm$

$A_{F}$	$=$	$\frac{1}{2} \cdot A_{K}$
	$=$	$\frac{1}{2} \cdot π \cdot r_{1}^{2}$
	$=$	$\frac{1}{2} \cdot π \cdot (5 cm)^{2}$
	$=$	$\frac{1}{2} \cdot π \cdot 25 {cm}^{2}$
	$=$	$12,5 \cdot π {cm}^{2}$
	↓	$π \approx 3,14$
	$\approx$	$12,5 \cdot 3,14 {cm}^{2}$
	$=$	$39,25 {cm}^{2}$

$U_{F}$	$=$	$U_{K} + 2 \cdot b$
	$=$	$2 \cdot π \cdot r + 2 \cdot b$
	$=$	$2 \cdot π \cdot 2 cm + 2 \cdot 10 cm$
	$=$	$4 \cdot π cm + 20 cm$
	↓	$π \approx 3,14$
	$\approx$	$4 \cdot 3,14 cm + 20 cm$
	$=$	$12,56 cm + 20 cm$
	$=$	$32,56 cm$

$U_{F}$	$=$	$b + h + U_{1} + U_{2} + U_{3}$
	$=$	$10 cm + 8 cm + (π + 2 π + 2 π) cm$
	$=$	$18 cm + 5 π cm$
	↓	$π \approx 3,14$
	$\approx$	$18 cm + 5 \cdot 3,14 cm$
	$=$	$33,7 cm$

$A_{K}$	$=$	$A_{K 1} + A_{K 2} + A_{K 3}$
	$=$	$(0,25 π + π + 2 π) {cm}^{2}$
	$=$	$3,25 π {cm}^{2}$
	↓	$π \approx 3,14$
	$\approx$	$3,25 \cdot 3,14 {cm}^{2}$
	$=$	$10,205 {cm}^{2}$
	$\approx$	$10,21 {cm}^{2}$

$A_{F}$	$=$	$A_{Q} + A_{K}$
	$=$	$26 {cm}^{2} + 10,21 {cm}^{2}$
	$=$	$36,21 {cm}^{2}$

Visuelle Aufgaben zu Kreisumfang und Kreisfläche

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?

Berechnung des Umfangs

Berechnung des Flächeninhaltes

Hast du eine Frage oder Feedback?