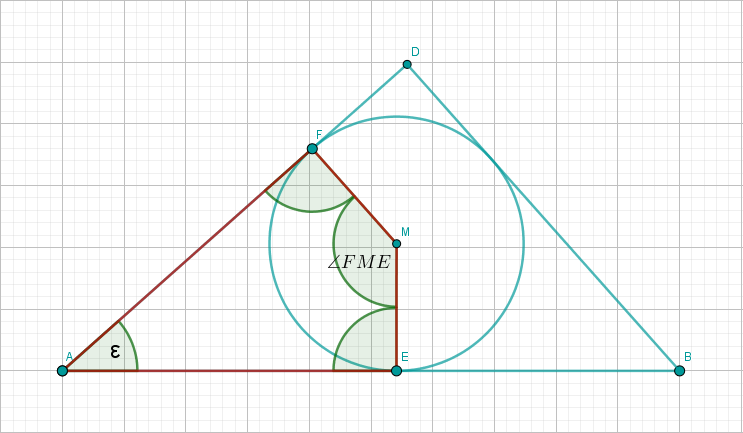
Gegeben ist das Dreieck mit und .
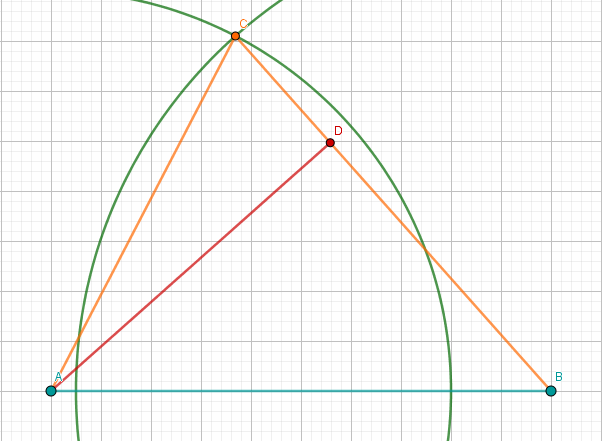
Der Punkt ist der Fußpunkt des Lotes vom Eckpunkt auf die Seite (siehe Skizze).
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
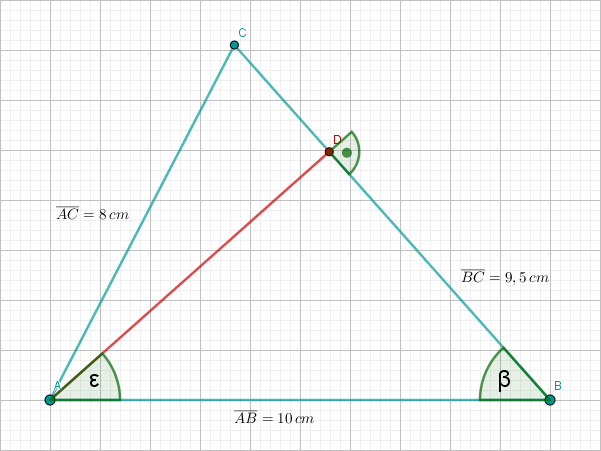
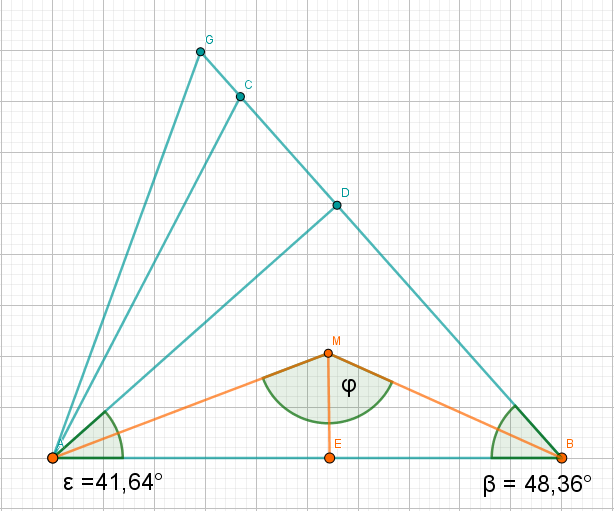
Zeichnen Sie das Dreieck und die Strecke .
Berechnen Sie das Maß des Winkels , das Maß des Winkels und die Länge der Strecke . Ergebnisse:
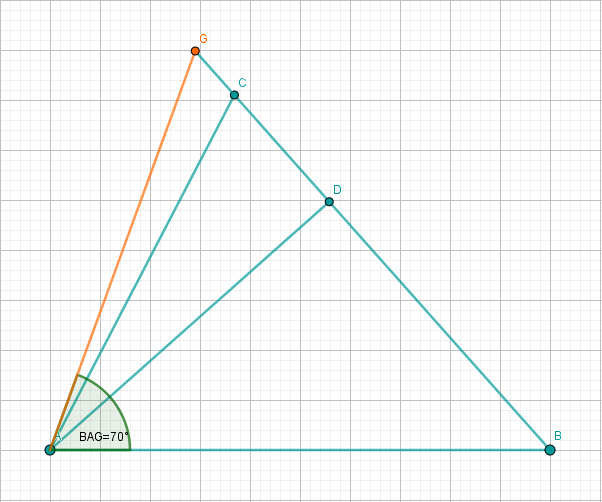
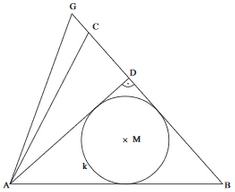
Der Punkt auf der Verlängerung der Strecke über hinaus ist ein Eckpunkt des Dreiecks . Der Winkel hat das Maß .
Zeichnen Sie das Dreieck und berechnen Sie die Länge der Strecke .
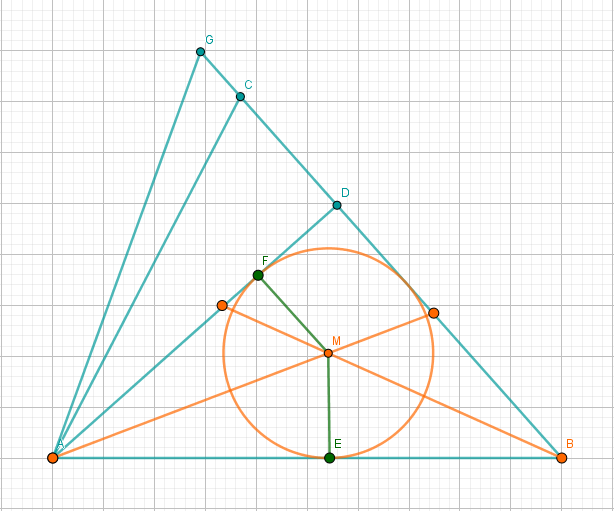
Im Dreieck berührt der Inkreis die Seite im Punkt und die Seite im Punkt .
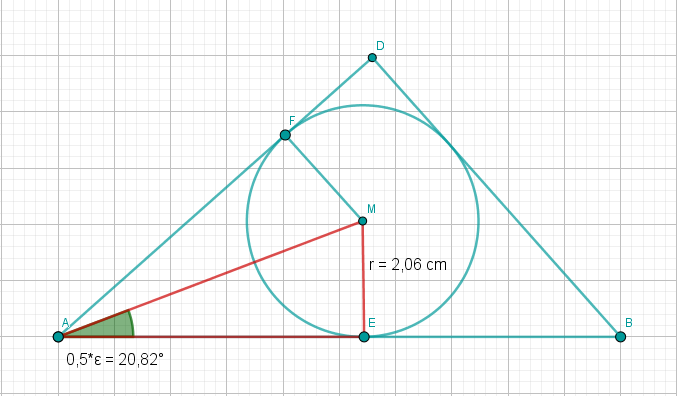
Zeichnen Sie den Inkreis mit seinem Mittelpunkt und die Strecken und in die Zeichnung zur Teilaufgabe a) ein.
Berechnen Sie das Maß des Winkels und den Inkreisradius .
Ergebnisse:
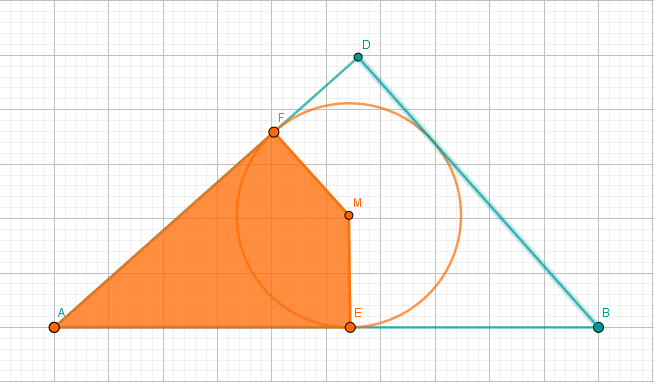
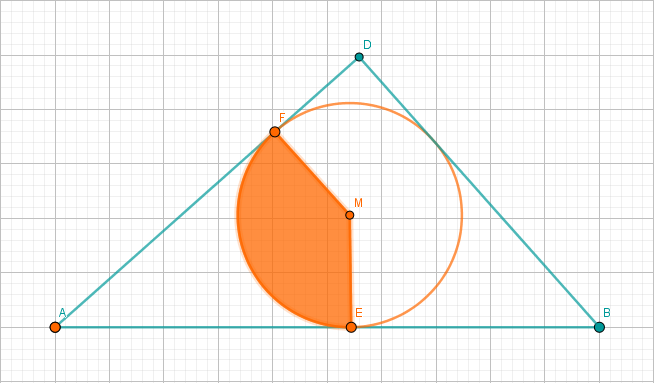
Berechnen Sie den Flächeninhalt des Flächenstücks , das vom Kreisbogen sowie von den Strecken und begrenzt wird.