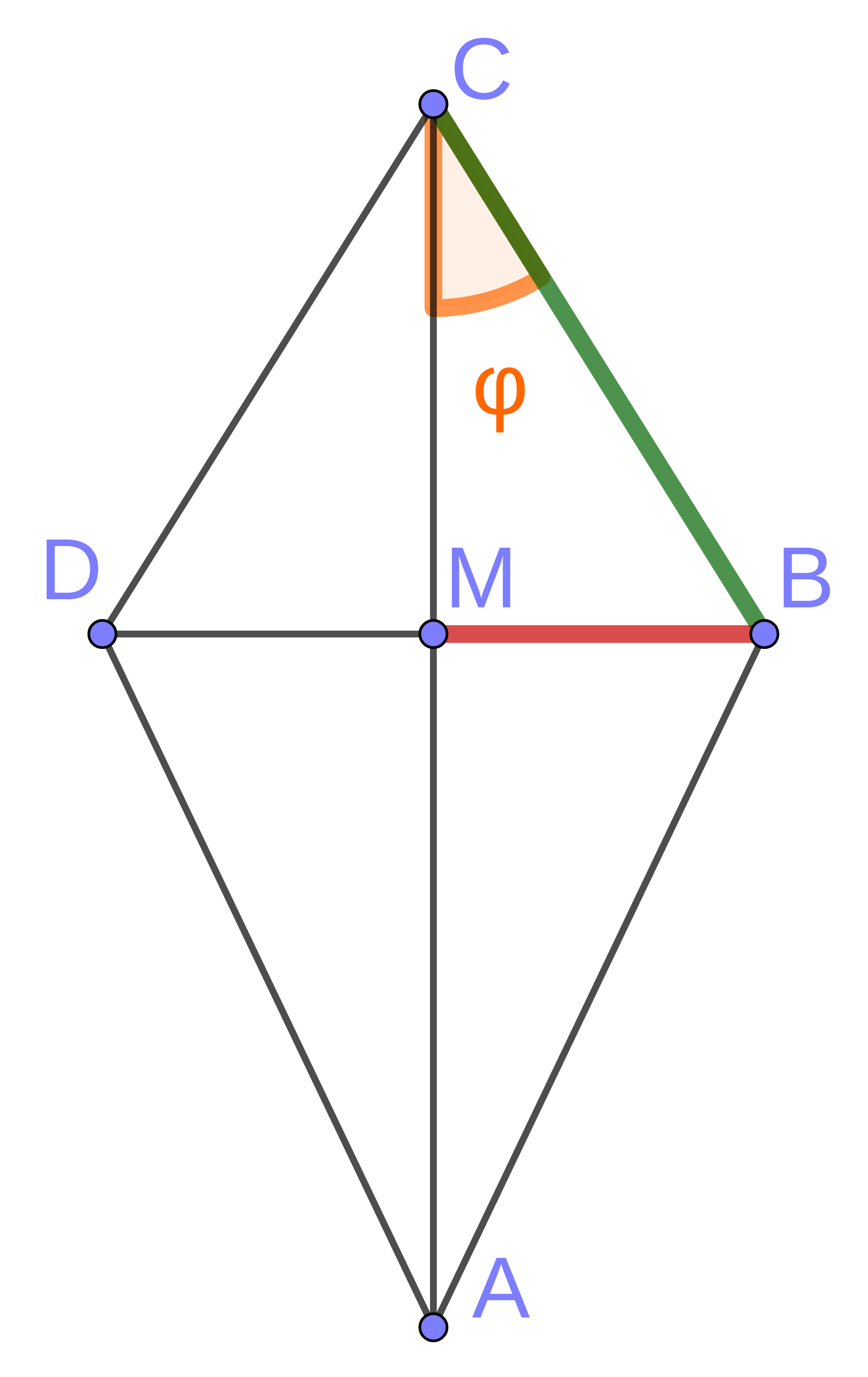
Pia möchte einen Flugdrachen bauen. Dazu erstellt sie nebenstehende Skizze eines Drachenvierecks mit der Symmetrieachse und dem Diagonalenschnittpunkt .
Es gilt:
Runden Sie im Folgenden auf Ganze.
Zeigen Sie rechnerisch, dass für das Maß des Winkels gilt:
Berechnen Sie die Länge der Diagonale und den Flächeninhalt des Drachenvierecks .
Ergebnis:
Da es im Baumarkt nur Holzstäbe mit einer Länge von gibt, beschließt Pia, für die Diagonale diese Länge zu verwenden. Die Diagonale bleibt unverändert.
Kreuzen Sie an, um wie viel Prozent sich der Flächeninhalt dadurch verringert.