Teil A - lernen mit Serlo!

Gegeben sind die Parabeln $p_{1}$ mit der Gleichung $y = 0,4 x^{2} - 1,8 x - 4$ und $p_{2}$ mit der Gleichung $y = - 0,2 x^{2} + 1,5 x + 1$ ( $𝔾 = ℝ \times ℝ$ ).

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

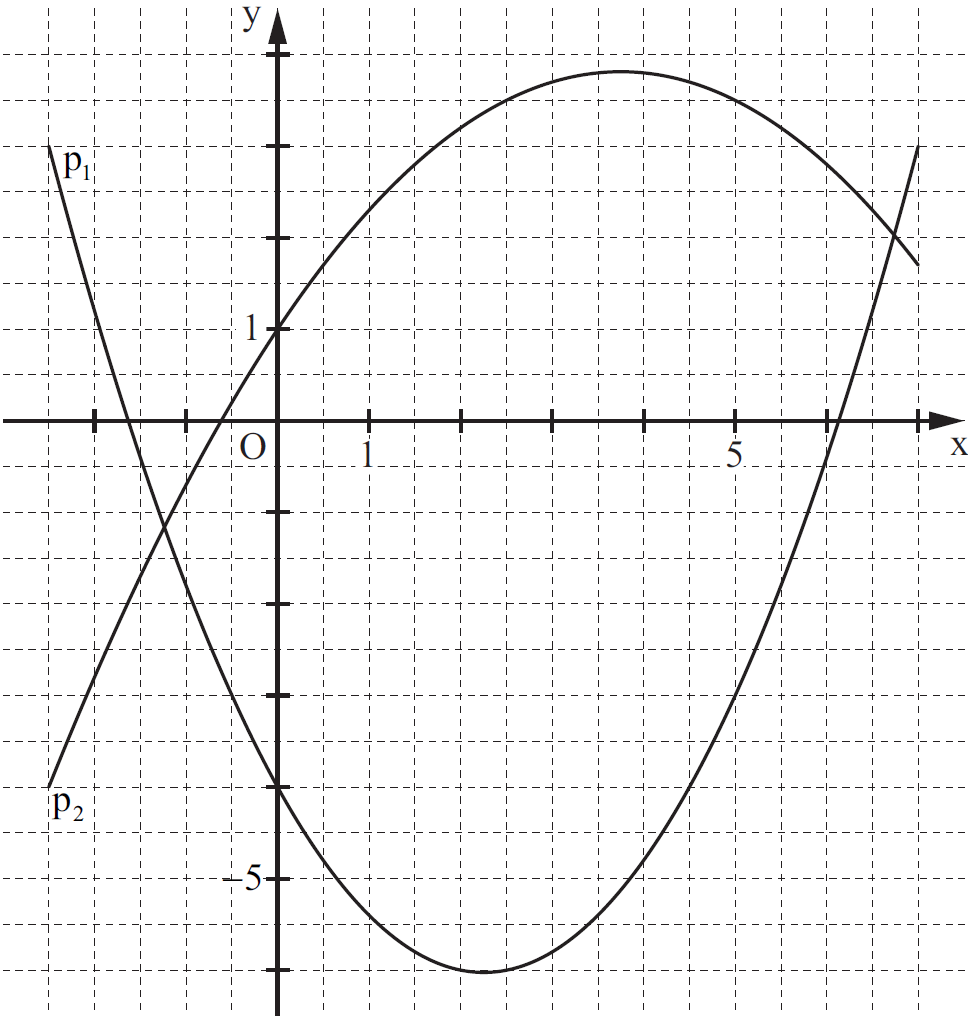
Punkte $B_{n} (x | 0,4 x^{2} - 1,8 x - 4)$ auf $p_{1}$ und Punkte $C_{n} (x | - 0,2 x^{2} + 1,5 x + 1)$ auf $p_{2}$ haben dieselbe Abszisse $x$ . Sie sind zusammen mit $A (0 | 1)$ für $x \in] 0; 6,74 [$ Eckpunkte von Dreiecken $A B_{n} C_{n}$ .
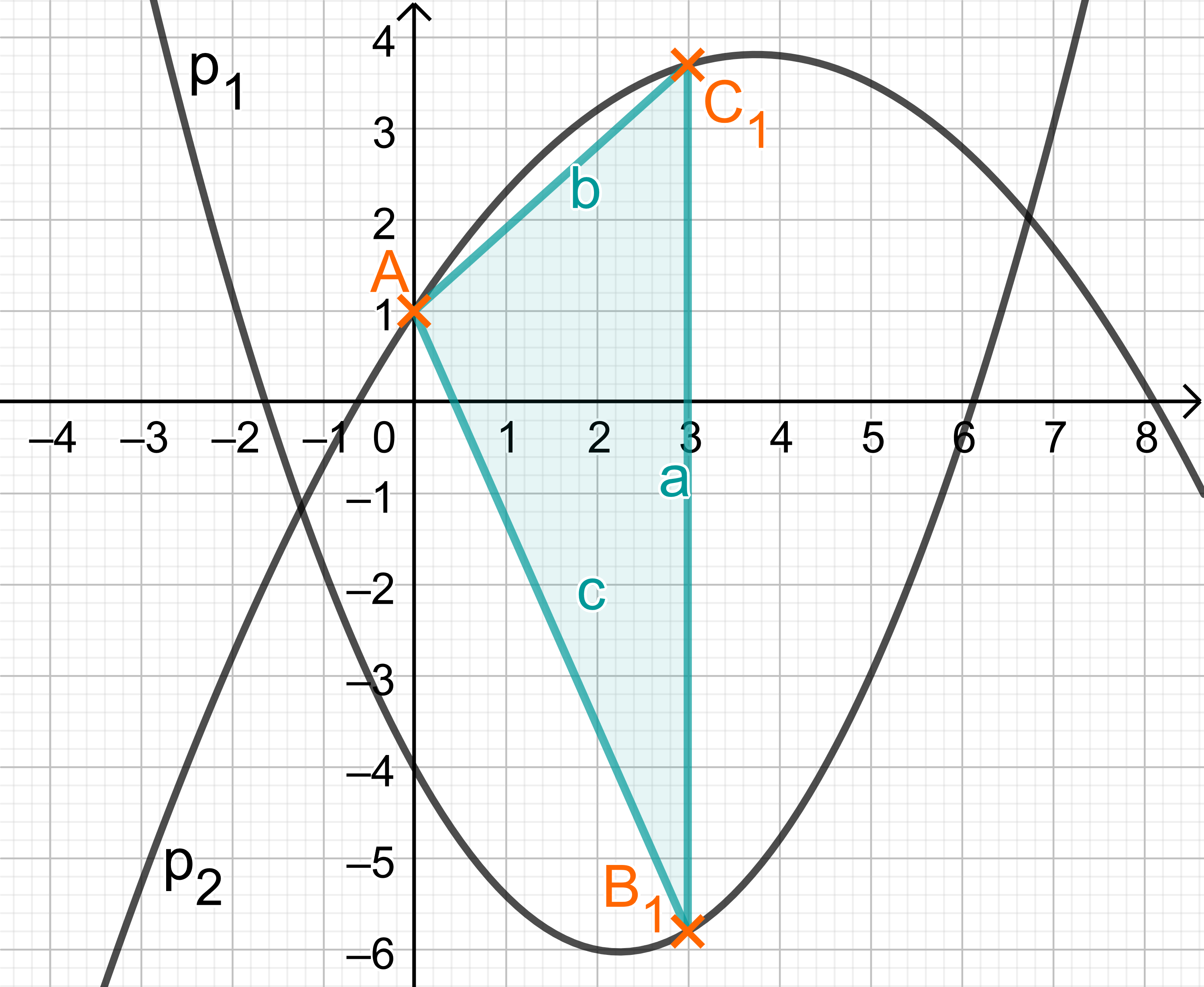
Zeichnen Sie das Dreieck $A B_{1} C_{1}$ für $x = 3$ in das Koordinatensystem zur Aufgabenstellung ein. Zeigen Sie sodann, dass für die Länge der Strecken $[B_{n} C_{n}]$ in Abhängigkeit von der Abszisse $x$ der Punkte $B_{n}$ gilt:
$B_{n} C_{n} (x) = (- 0,6 x^{2} + 3,3 x + 5)$ LE.

Graphischer Ansatz
Zuerst kannst du das Dreieck $A B_{1} C_{1}$ einzeichnen. Für den Punkt $C_{1}$ suchst du dabei auf der $x$ -Achse den Wert $x = 3$ und gehst dann senkrecht nach oben bis zur Parabel $p_{2}$ , dort kannst du ihn dann einzeichnen. Für $B_{1}$ machst du das Gleiche, gehst aber nach unten bis zur Parabel $p_{1}$ .
Rechnerischer Ansatz
Du kannst die Koordinaten von $B_{1}$ und $C_{1}$ auch dadurch bestimmen, dass du den Wert $x = 3$ in die Formeln aus der Angabe einsetzt:
$\begin{array}{c} B_{n} (x | 0,4 x^{2} - 1,8 x - 4) & \Rightarrow & B_{1} (3 | 0,4 \cdot 3^{2} - 1,8 \cdot 3 - 4) \\ C_{n} (x | - 0,2 x^{2} + 1,5 x + 1) & \Rightarrow & C_{1} (3 | - 0,2 \cdot 3^{2} + 1,5 \cdot 3 + 1) \end{array}$
So erhältst du die Punkte $B_{1} (3 | - 5,8)$ und $C_{1} (3 | 3,7)$ , die du jetzt ganz leicht einzeichnen kannst.
Nun geht es noch darum die Länge der Strecke $B_{n} C_{n} (x)$ zu bestimmen. Dazu bildest du die Differenz der Funktionsterme der beiden Parabeln, und zwar $p_{2} - p_{1}$ , weil $p_{2}$ in diesem Bereich oberhalb von $p_{1}$ verläuft:
$B_{n} C_{n} (x)$ $=$ $[\overset{y-Wert von C_{n}}{\overset{⏞}{- 0,2 x^{2} + 1,5 x + 1}} - \overset{y-Wert von B_{n}}{\overset{⏞}{(0,4 x^{2} - 1,8 x - 4)}}] LE$
$=$ $(- 0,6 x^{2} + 3,3 x + 5) LE$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Begründen Sie, weshalb es unter den Dreiecken $A B_{n} C_{n}$ kein Dreieck $A B_{0} C_{0}$ gibt, dessen Seite $[B_{0} C_{0}]$ eine Länge von $10$ LE besitzt.

Hier solltest du als Erstes versuchen den Wert für $x$ zu bestimmen, so dass die Strecke die Länge $10$ LE besitzt. Setze dazu den Wert $10$ mit der Formel für die Länge der Strecke aus Teilaufgabe a gleich:
$\begin{array}{c} 10 & = & - 0,6 x^{2} + 3,3 x + 5 \\ 0 & = & - 0,6 x^{2} + 3,3 x - 5 \end{array}$
Diese Gleichung kannst du nun mithilfe der Mitternachtsformel lösen. Dafür brauchst du auch die Diskriminante der Gleichung:
$D = {3,3}^{2} - 4 \cdot (- 0,6) \cdot (- 5) = - 1,11$
Da die Diskriminante negativ ist, besitzt die Gleichung keine Lösung. Deshalb kannst du auch kein Dreieck $A B_{n} C_{n}$ finden, bei dem die Seite $[B_{n} C_{n}]$ die Länge $10$ LE besitzt.
Im folgenden Applet kannst du die Punkte $B_{n}$ und $C_{n}$ frei bewegen und dir ansehen, wie sich die Länge von $[B_{n} C_{n}]$ verändert:
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
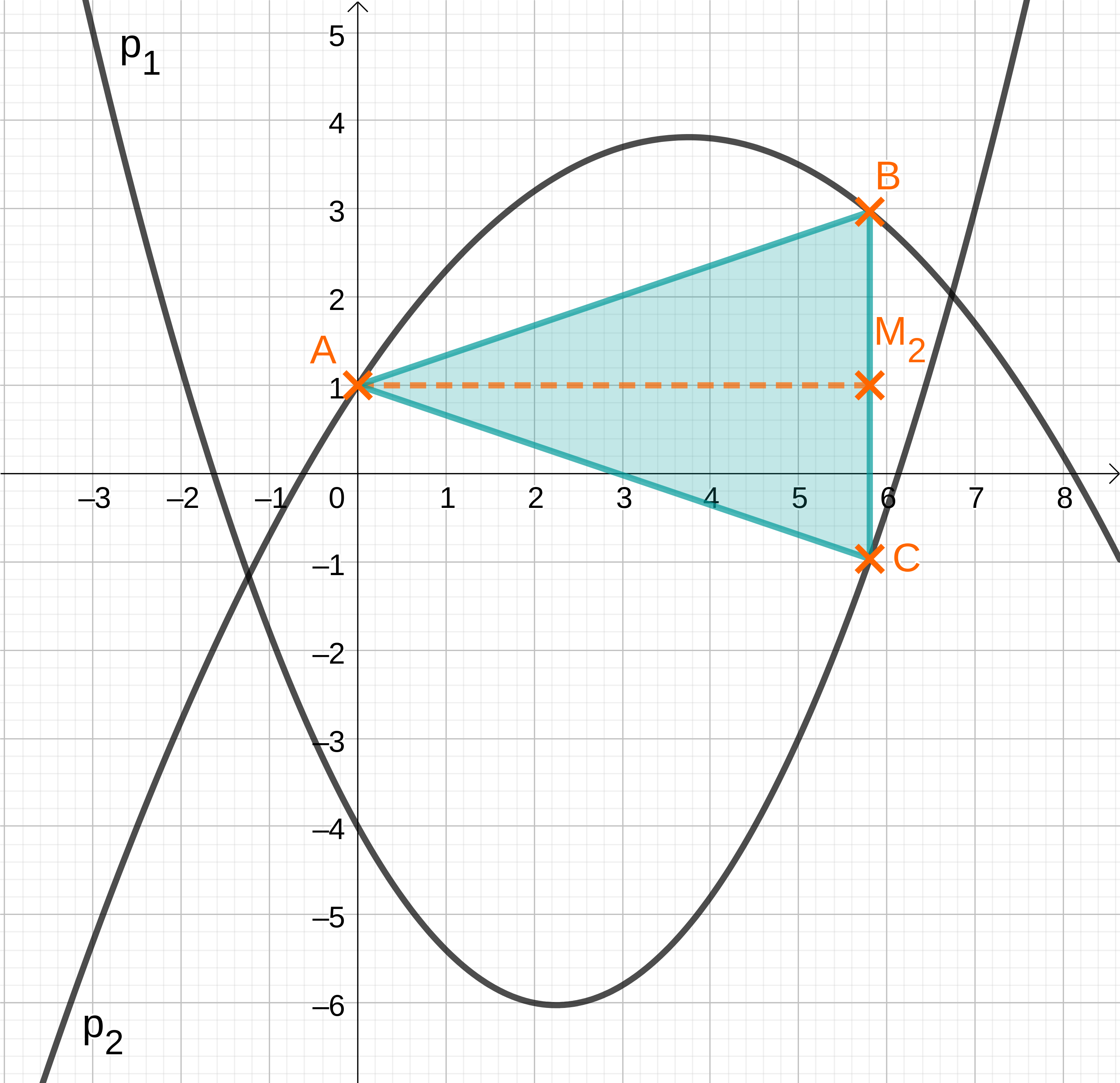
Die Mittelpunkte $M_{n}$ der Seiten $[B_{n} C_{n}]$ haben dieselbe Abszisse $x$ wie die Punkte $B_{n}$ . Zeigen Sie, dass für die $y$ -Koordinate $y_{M}$ der Punkte $M_{n}$ gilt:
$y_{M} = 0,1 x^{2} - 0,15 x - 1,5.$

Die Punkte $M_{n}$ sind Mittelpunkte der Strecken $[B_{n} C_{n}]$ , ihre Koordinaten kannst du als den Mittelwert der Koordinaten von $B_{n}$ und $C_{n}$ berechnen. Es gilt also: $x_{M_{n}} = \frac{1}{2} (x_{C_{n}} + x_{B_{n}})$ und für die $y$ -Koordinaten:
$\begin{array}{c} y_{M_{n}} = \frac{1}{2} \cdot (y_{C_{n}} + y_{B_{n}}) = \frac{1}{2} (- 0,2 x^{2} + 1,5 x + 1 + 0,4 x^{2} - 1,8 x - 4) \\ y_{M_{n}} = \frac{1}{2} \cdot (0,2 x^{2} - 0,3 x - 3) = 0,1 x^{2} - 0,15 x - 1,5 \end{array}$
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Das Dreieck $A B_{2} C_{2}$ ist gleichschenklig mit der Basis $[B_{2} C_{2}]$ .
Berechnen Sie die $x$ -Koordinate des Punktes $M_{2}$ .

Die Basis des Dreiecks ist die Strecke $[B_{2} C_{2}]$ , da $B_{2}$ und $C_{2}$ dieselbe Abszisse haben und das Dreieck gleichschenklig ist, haben der Punkt $A$ und der Punkt $M_{n}$ die selbe y-Koordinate. Es gilt also:
$1 = y_{M_{n}} = 0,1 x^{2} - 0,15 x - 1,5 0 = 0,1 x^{2} - 0,15 x - 2,5$
Diese Gleichung ist wieder mit der Mitternachtsformel lösbar:
$x_{1,2} = \frac{0,15 \pm \sqrt{{0,15}^{2} - 4 \cdot 0,1 \cdot (- 2,5)}}{2 \cdot 0,1}$
Du erhältst die Werte $x_{1} = 5,81$ und $x_{2} = - 4,31$ . In der Angabe wurde geklärt, dass $x$ nur positive Werte annehmen soll, deshalb ist die $x$ -Koordinate des Punkts $M_{n}$ also $x_{M_{n}} = 5,81$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?

$B_{n} C_{n} (x)$	$=$	$[\overset{y-Wert von C_{n}}{\overset{⏞}{- 0,2 x^{2} + 1,5 x + 1}} - \overset{y-Wert von B_{n}}{\overset{⏞}{(0,4 x^{2} - 1,8 x - 4)}}] LE$
	$=$	$(- 0,6 x^{2} + 3,3 x + 5) LE$

Graphischer Ansatz

Rechnerischer Ansatz

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?