Nachtermin Teil B

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

Nutze unser Training Realschule Bayern (Abschlussprüfung) und rechne dich fit für die Prüfung. Du findest dort einen Überblick über alle Themen und viele weitere Übungsmöglichkeiten.

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe B1
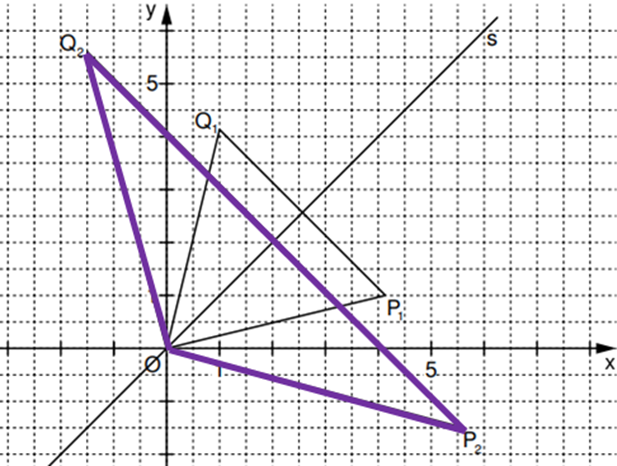
Pfeile $\vec{O P_{n}} (φ) = (\begin{array}{c} 5 - \sin φ \\ 2 \cdot \cos φ \end{array})$ und $\vec{O Q_{n}}$ mit $O (0 | 0)$ spannen für $φ \in [0^{\circ}; 360^{\circ}]$ gleichschenklige Dreiecke $O P_{n} Q_{n}$ mit den Basen $P_{n} Q_{n}$ auf. Die Gerade $s$ mit der Gleichung $y = x (x, y \in ℝ)$ ist die Symmetrieachse der Dreiecke $O P_{n} Q_{n}$ .
In das Koordinatensystem ist das Dreieck $O P_{1} Q_{1}$ für $φ = 60^{\circ}$ bereits eingezeichnet.
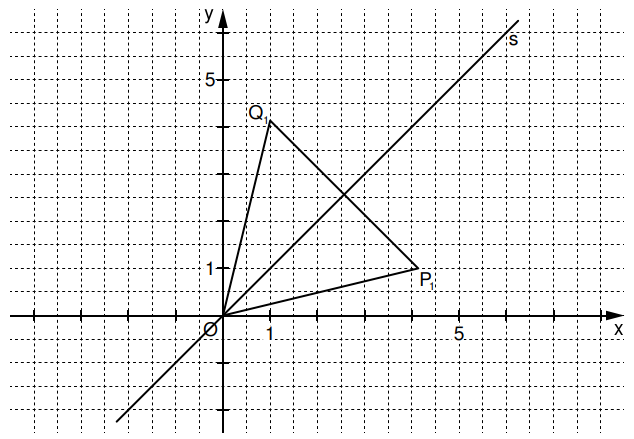
1. Geben Sie die Koordinaten des Pfeils $\vec{O P_{2}}$ für $φ = 220^{\circ}$ an und zeichnen Sie das Dreieck $O P_{2} Q_{2}$ in die Zeichnung zur Aufgabenstellung ein.
  Runden Sie auf eine Nachkommastelle. (2 P)
  
  geg.: gleichschenkliges Dreieck $O P_{1} Q_{1}$ mit $φ = 60 °$ und Symmetrieachse $S : y = x$
  ges.: Koordinaten $\vec{O P_{2}}$ und Zeichnung $△ O P_{2} Q_{2}$ für $φ = 220^{\circ}$
  Ansatz und Rechnung:
  1. Koordinaten von $\vec{O P_{2}} (φ = 220^{\circ})$
  $\vec{O P_{2}} (φ = 220^{\circ}) = (\begin{array}{c} 5 - \sin (220 °) \\ 2 \cdot \cos (220 °) \end{array}) \approx (\begin{array}{c} 5 - (- 0,643) \\ 2 \cdot (- 0,766) \end{array})$
  $= (\begin{array}{c} 5,643 \\ - 1,532 \end{array}) \approx (\begin{array}{c} 5,6 \\ - 1,5 \end{array})$
  2. Zeichnung $△ O P_{2} Q_{2}$
  $\vec{O P_{2}} (φ = 220^{\circ}) = (\begin{array}{c} 5,6 \\ - 1,5 \end{array})$ einzeichnen; $Q_{2}$ symmetrisch zur Symmetrieachse $S : y = x$
  Zeichnung der Dreiecke $O P_{1} Q_{1}$ mit $φ = 60 °$ und $O P_{2} Q_{2}$ mit $φ = 220 °$
  Skizze mit dem Dreieck $O P_{2} Q_{2}$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Koordinaten berechnen, gleichschenkliges Dreieck zeichnen
2. Für die Dreiecke $O P_{3} Q_{3}$ und $O P_{4} Q_{4}$ gilt: $∢ P_{3} O Q_{3} = ∢ P_{4} O Q_{4} = 90^{\circ}$ .
  Bestimmen Sie die zugehörigen Werte von $φ$ . (2 P)
  
  geg.: gleichschenklige Dreiecke $O P_{3} Q_{3}$ und $O P_{4} Q_{4}$ mit $∢ P_{3} O Q_{3} = ∢ P_{4} O Q_{4} = 90^{\circ}$
  ges.: Wert $φ$
  Ansatz & Rechnung
  Setze für beide Dreiecke $O P_{3} Q_{3}$ und $O P_{4} Q_{4}$ die $y$ -Komponente von $\vec{O P_{n}} (φ) = (\begin{array}{c} 5 - \sin φ \\ \blue 2 \cdot \cos φ \end{array})$ gleich null:
  $y_{P 3, P 4} = 0 = \blue 2 \cdot \cos φ$ für $φ \in [0 °; 360 °]$
  $\Rightarrow$ im Bereich $φ \in [0 °; 360 °]$ ist die Gleichung erfüllt für $c o s (\frac{π}{2}) ≙ 0$ und für $c o s (\frac{3}{2} π) ≙ 0$
  Damit muss $φ = 90 °$ oder $φ = 270 °$ sein.
  $𝕃 = {90^{\circ}; 270^{\circ}}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bestimme $φ$ durch den Vektor $O P_{n} (φ)$ . Wenn der Winkel im Punkt $O$ $90^{\circ}$ ist, dann muss der Vektor auf der x-Achse liegen. Setze also den $y$ -Wert des Vektors gleich 0.
3. Begründen Sie, weshalb es unter den Dreiecken $O P_{n} Q_{n}$ kein Dreieck $O P_{5} Q_{5}$ mit $P_{5} (3 | 3)$ gibt. (1 P)
  
  Nachweis
  Der Punkt $P_{5} (3 | 3)$ liegt auf der Symmetrieachse, die durch $y = x$ gegeben ist.
  Wenn $P_{5} (3 | 3)$ auf der Symmetrieachse $s$ liegt, liegen auch $Q_{5}$ und $O$ darauf. Das ergibt kein Dreieck.
  $\Rightarrow$ Es gibt kein Dreieck $O P_{5} Q_{5}$ mit $P_{5} (3 | 3)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Skizziere den Punkt in das Koordinatensystem.
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe B2
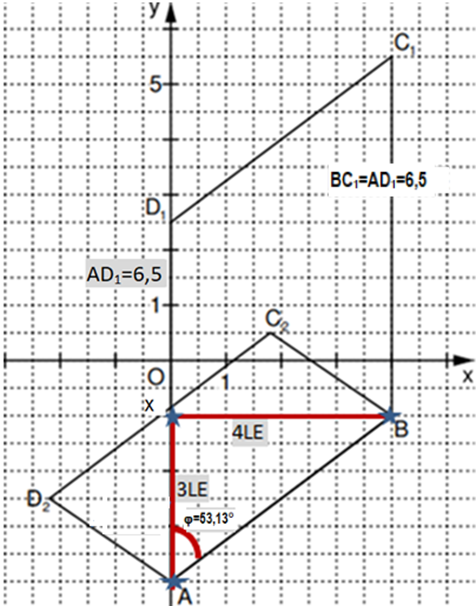
Das gleichschenklige Dreieck $A B C$ mit der Basis $A B$ ist die Grundfläche der Pyramide $A B C S$ mit der Höhe $R S (R \in A B)$ .
Der Punkt $M$ ist der Mittelpunkt der Basis $A B$ .
Es gilt: $A B = 6 cm$ ; $M C = 4 cm$ ;
$A S = 5,5 cm$ ; $R S = 5 cm$ .
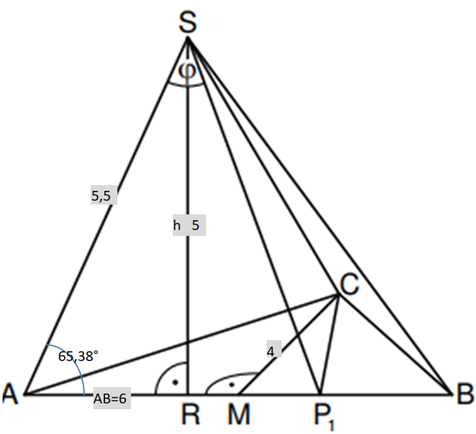
Die Zeichnung zeigt ein Schrägbild der Pyramide $A B C S$ .
In der Zeichnung gilt:
$q = \frac{1}{2}$ ; $ω = 45^{\circ}$ ; $A B$ liegt auf der Schrägbildachse.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
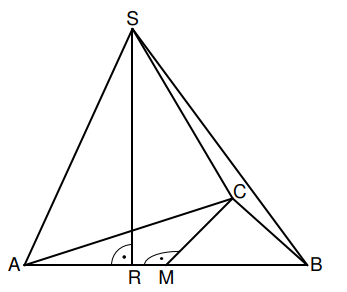
1. Berechnen Sie das Maß des Winkels $B A S$ . (1 P)
  $[$ Ergebnis: $∢ B A S = {65,38}^{\circ}]$
  
  geg.: $△ A B C$ gleichschenklig mit Basis $A B = 6 c m$ , als Grundfläche der Pyramide ABCS,
  $h_{P y r a m i d e} = R S = 5 c m$ (mit $R \in A B$ , $M =$ Mittelpunkt $A B$ ;
  Schrägbild mit Schrägbildachse $A B$ , mit $q = 0,5$ und $ω = 45 °$ ;
  $| M C | = 4 c m$ ; $| A S | = 5,5 c m$ ;
  ges.: Zeichnung aus Aufgabenstellung ergänzen, $∢ B A S$ berechnen
  Ansatz und Rechnung:
  1. Schrägbild der Pyramide ergänzen:
  Schrägbild Pyramide ABCS
  2. Winkel BAS berechnen:
  aus Zeichnung $∢ B A S ≙ ∢ R A S$ ; Berechnung $∢ B A S$ mithilfe Sinus
  $\Rightarrow \sin ∢ B A S = [\frac{G K}{H Y}] = \frac{R S}{A S} = \frac{5}{5,5} = 0,9090$
  $\Rightarrow ∢ 𝐁 𝐀 𝐒 = 𝟔𝟓,𝟑𝟖 °$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Zeichnung mit gegebenen Werten ergänzen und Winkel BAS berechnen
2. Punkte $P_{n}$ liegen auf der Strecke $A B$ . Die Winkel $A S P_{n}$ haben das Maß $φ$ mit
  $φ \in] 0^{\circ}; {61,18}^{\circ}]$ .
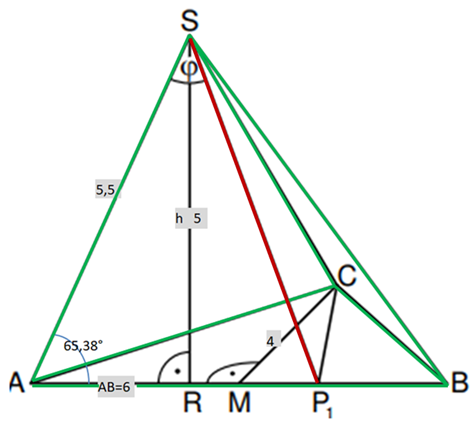
  Zeichnen Sie die Strecke $S P_{1}$ für $φ = 45^{\circ}$ in das Schrägbild zur Aufgabenstellung ein.
  Zeigen Sie sodann, dass für die Länge der Strecken $S P_{n}$ in Abhängigkeit von $φ$ gilt:
  $| S P_{n} | (φ) = \frac{5}{\sin ({65,38}^{\circ} + φ)} cm .$ (2,5 P)
  
  geg.: $∢ A S P_{n} = φ$ mit $φ \in] 0 °; 61,18 °]$
  ges.:
  1. Einzeichnung Strecke $S P_{1}$ für $φ = 45 °$ in das Schrägbild der Pyramide
  2. Berechnung $S P_{n} (φ)$ mit Sinus-Supplementwinkel-Beziehung
  Ansatz und Rechnung:
  1. Schenkel in $S$ mit $45 °$ an Strecke $A S$ schneidet Strecke $A B$ in $P_{1}$
  Schrägbild Pyramide mit Strecke $S P_{1}$
  2. Berechnung $S P_{n} (φ)$ mit Sinus-Supplementwinkel-Beziehung
  $\sin (180 ° - (φ + ∢ B A S)) = \frac{| R S |}{| S P_{n} |} = \frac{5 c m}{| S P_{n} |}$ für $φ \in] 0 °; 61,18 °]$
  Entsprechend der Supplementwinkel-Beziehung $\sin (180 ° - α) = \sin (α)$
  ergibt sich für $\sin (180 ° - (φ + ∢ B A S)) = \sin (φ + ∢ B A S)$
  $\Rightarrow \sin (φ + 65,38 °) = \frac{5 c m}{| S P_{n} |}$
  nach Äquivalenzumformung (Multiplikation mit $| S P_{n} |$ und Division durch $\sin (φ + 65,38 °)$ ) folgt
  $| 𝐒 𝐏_{𝐧} | (𝛗) = \frac{𝟓}{\sin (𝛗 + 𝟔𝟓,𝟑𝟖 °)} 𝐜 𝐦$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Pyramide mit gegebenen Werten ergänzen,
  Streckenberechnung mithilfe der Sinus-Supplementwinkel-Beziehung
3. Die Dreiecke $A P_{n} S$ sind die Grundflächen von Pyramiden $A P_{n} S C$ mit der Spitze $C$ .
  Zeichnen Sie die Pyramide $A P_{1} S C$ in die Zeichnung zur Aufgabenstellung ein.
  Berechnen Sie sodann das Volumen $V$ der Pyramiden $A P_{n} S C$ in Abhängigkeit von $φ$ . (2,5 P)
  
  ges.:
  1. Pyramide $A P_{1} S C$ mit C als Spitze $\Rightarrow h ≙ | M C | = 4 c m$
  2. . Volumen $V (φ)$ der Pyramiden $A P_{n} S C$
  Ansatz und Rechnung:
  1. Pyramide $A P_{1} S C$ siehe Skizze in Aufgabe B a)
  2. Volumen der Pyramiden $A P_{n} S C$
  $𝐕_{Pyr} = \frac{𝟏}{𝟑} \cdot 𝐆_{𝐀 𝐏_{𝐧} 𝐒} \cdot 𝐡$
  $G_{A P_{n} S}$ mithilfe Sinussatz: $𝐆 = \frac{𝟏}{𝟐} \cdot 𝐜 \cdot 𝐛 \cdot \sin (𝛂)$
  $\Rightarrow G_{A P_{n} S} = \frac{1}{2} \cdot | A S | \cdot | S P_{n} | (φ) \cdot \sin (φ)$
  mit $h ≙ M C = 4 c m$ , $| A S | = 5,5 c m$ und $| S P_{n} | (φ) = \frac{5}{\sin (65,38 ° + φ)} c m$
  eingestzt in $V_{Pyr}$ ergibt das
  $\Rightarrow V_{Pyr} (φ) = \frac{1}{3} \cdot \frac{1}{2} \cdot | A S | \cdot | S P_{n} | (φ) \cdot \sin (φ) \cdot 4$
  $\Rightarrow V_{Pyr} (φ) = \frac{1}{3} \cdot \frac{1}{2} \cdot 5,5 \cdot \frac{5}{\sin (65,38 ° + φ)} \cdot \sin (φ) \cdot 4 [c m^{3}]$ mit $φ \in] 0 °; 61,18 °]$
  $\Rightarrow 𝐕_{Pyr} (𝛗) = 𝟏𝟖,𝟑𝟑 \cdot \frac{𝐬 𝐢 𝐧 (𝛗)}{\sin (𝟔𝟓,𝟑𝟖 ° + 𝛗)} [c m^{3}]$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Pyramide $A P_{1} S C$ zeichnen und Volumen $V (φ)$ berechnen
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe B3
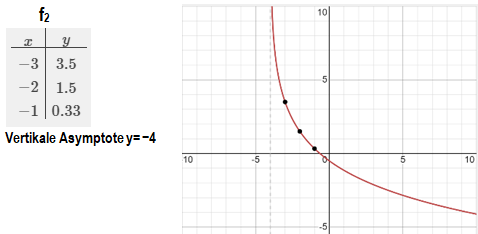
Gegeben ist die Funktion $f_{1}$ mit der Gleichung $y = - 2 \cdot \log_{0,5} (x + 3) + 1,5$ und $x$ , $y \in ℝ$ .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
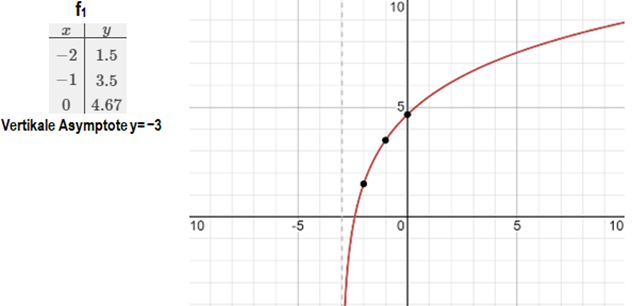
1. Geben Sie die Wertemenge der Funktion $f_{1}$ und die Gleichung der Asymptote $h$ des Graphen zu $f_{1}$ an.
  Zeichnen Sie zudem den Graphen zu $f_{1}$ für $x \in [- 2,5; 5]$ in ein Koordinatensystem ein. (3 P)
  Für die Zeichnung: Längeneinheit $1 cm$ ; $- 3 \leq x \leq 5; - 3 \leq y \leq 8$
  
  geg.: $y = - 2 \cdot \log_{0,5} (x + 3) + 1,5$ jeweils mit $x, y \in ℝ$
  Anwendung der Identität von $\log_{0,5} (. . .) ≙ \log_{\frac{1}{2}} (. . .) ≙ - \log_{2} (. . .)$ auf $f_{1}$
  $\Rightarrow y = - 2 \cdot (- \log_{2} (x + 3)) + 1,5$
  $\Rightarrow y = 2 \cdot \log_{2} (x + 3) + 1,5$
  Für die Zeichung gilt: $L E ≙ 1 c m; - 3 \leq x \leq 5; - 3 \leq y \leq 8$
  ges.:
  1. Wertemenge $W$ von $f_{1}$
  2. Gleichung der Asymptote $h$ des Graphen von $f_{1}$ für $x \in [- 2,5; 5]$
  Ansatz und Rechnung:
  1. Wertemenge: $𝕎 = ℝ$
  2. Graph: gezeichnet mit https://www.mathway.com
  Graph von $f_{1}$ mit Asymptote $h$
  
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Schreibe den Logarithmus auf einen mit der Basis $2$ um.
  Benutze, dass alle Logarithmen bei Null eine senkrechte Asymptote haben.
2. Der Graph der Funktion $f_{1}$ wird durch Achsenspiegelung an der x-Achse sowie
  anschließende Parallelverschiebung mit dem Vektor $\vec{v} = (\begin{array}{c} - 1 \\ 5 \end{array})$ auf den Graphen der Funktion $f_{2}$ abgebildet.
  Zeigen Sie rechnerisch, dass die Funktion $f_{2}$ die Gleichung $y = 2 \cdot \log_{0,5} (x + 4) + 3,5$ $(x, y \in ℝ)$ besitzt und zeichnen Sie den Graphen zu $f_{2}$ für $x \in [- 3; 5]$ in das Koordinatensystem zu a) ein. (3 P)
  
  geg.: Funktionsgraph $f_{1}$ ; Verschiebungsvektor $\vec{v} = (\begin{array}{c} - 1 \\ 5 \end{array})$
  ges.: $f_{2}$ (=gespiegelte und parallel verschobene $f_{1}$ ) mit Graph
  Ansatz und Rechnung:
  1. Spiegelung $f_{1}$ an x-Achse durch Multiplikation des Funktionsterms mit $- 1$
  $\Rightarrow (\begin{array}{c} x^{^{'}} \\ y^{^{'}} \end{array}) = (\begin{array}{c} x \\ - 1 \cdot (- 2 \cdot \log_{0,5} (x + 3) + 1,5 \end{array}) x, x ‘, y ‘ \in ℝ$
  $x^{'} = x$ einsetzen in $y^{'}$ :
  $\Rightarrow 𝐟_{𝟏 gespiegelt} : 𝐲^{^{'}} = 𝟐 \cdot \log_{𝟎,𝟓} (𝐱 + 𝟑) - 𝟏,𝟓$
  Jetzt kann man natürlich wieder $y^{'}$ in $y$ umbenennen:
  $𝐟_{𝟏 gespiegelt} : 𝐲 = 𝟐 \cdot \log_{𝟎,𝟓} (𝐱 + 𝟑) - 𝟏,𝟓$
  2. Parallelverschiebung der gespiegelten Funktion durch Vektoraddition
  mit $\vec{v} = (\begin{array}{c} - 1 \\ 5 \end{array})$
  $\Rightarrow (\begin{array}{c} x^{^{'}} \\ y^{^{'}} \end{array}) = (\begin{array}{c} x \\ 2 \cdot \log_{0,5} (x + 3) - 1,5 \end{array}) \oplus︎ (\begin{array}{c} - 1 \\ 5 \end{array}) x, x ‘, y ‘ \in ℝ$
  $x^{'} = x - 1 \Rightarrow x = x^{'} + 1$ eingesetzt in $y^{'}$
  $y^{^{'}} = 2 \cdot \log_{0,5} (x + 1 + 3) - 1,5 + 5 = 2 \cdot \log_{0,5} (x + 4) + 3,5 𝔾 = ℝ x ℝ$
  Jetzt wird wieder $y^{'}$ in $y$ umbenannt:
  $\Rightarrow f_{2} : y = 2 \cdot \log_{0,5} (x + 4) + 3,5 x, y \in ℝ$
  Anwendung der Identität von $\log_{0,5} (. . .) ≙ \log_{\frac{1}{2}} (. . .) ≙ - \log_{2} (. . .)$
  $\Rightarrow 𝐟_{𝟐 𝐯 𝐞 𝐫 𝐬 𝐜 𝐡 𝐨 𝐛 𝐞 𝐧} 𝐲 = - 𝟐 \cdot \log_{𝟐} (𝐱 + 𝟒) + 𝟑,𝟓$
  3. Einzeichnen des Graphen zu $f_{2}$ für $x \in [- 3; 5] :$
  Graph wurde gezeichnet mit https://www.mathway.com
  Graph von $f_{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  1. Spiegelung von $f_{1}$ an x-Achse;
  2. Parallelverschiebung von $f_{1}$ ;
  3. Graph der gespiegelten und verschobenen Funktion $f_{2}$ ins KOSY einzeichnen
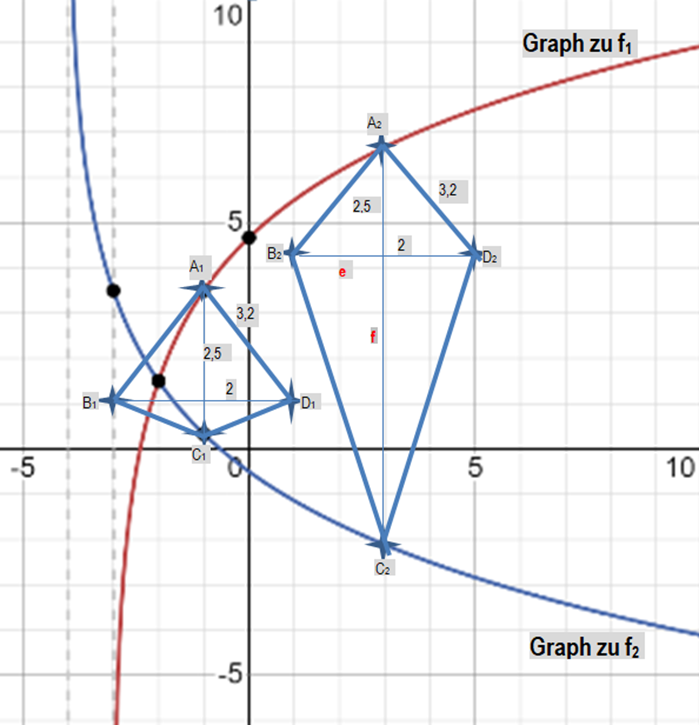
3. Punkte $A_{n} (x | - 2 \cdot \log_{0,5} (x + 3) + 1,5)$ auf dem Graphen zu $f_{1}$ haben dieselbe Abszisse $x$ wie Punkte $C_{n} (x | 2 \cdot \log_{0,5} (x + 4) + 3,5)$ auf dem Graphen zu $f_{2}$ . Sie sind für $x > - 1,26$ zusammen mit Punkten $B_{n}$ und $D_{n}$ die Eckpunkte von Drachenvierecken $A_{n} B_{n} C_{n} D_{n}$ mit den Symmetrieachsen $A_{n} C_{n}$ .
  Es gilt: $\vec{A_{n} B_{n}} = (\begin{array}{c} - 2 \\ - 2,5 \end{array})$ .
  Zeichnen Sie die Drachenvierecke $A_{1} B_{1} C_{1} D_{1}$ für $x = - 1$ und $A_{2} B_{2} C_{2} D_{2}$ für $x = 3$ mit ihren Diagonalen in das Koordinatensystem zu a) ein. (2 P)
  
  geg.: $A_{n} (x │ - 2 \cdot \log_{0,5} (x + 3) + 1,5)$ auf $f_{1}$ und $C_{n} (x │ 2 \cdot \log_{0,5} (x + 4) + 3,5)$ auf $f_{2}$ sind für $x > - 1,26$ mit den Punkten $B_{n}$ und $D_{n}$ die Eckpunkte von Drachenvierecken $A_{n} B_{n} C_{n} D_{n}$ mit den Symmetrieachsen $A_{n} C_{n}$
  ges.: Zeichnung der Drachenvierecke $A_{1} B_{1} C_{1} D_{1}$ für $x = - 1$ und $A_{2} B_{2} C_{2} D_{2}$ für $x = 3$ mit ihren Diagonalen $A_{n} C_{n}$ und $B_{n} D_{n}$ ins KOSY
  Ansatz & Rechnung:
  1. Eckpunkte $A_{1}$ und $C_{1}$ für $x = - 1$ sowie $A_{2}$ und $C_{2}$ für $x = 3$ berechnen und einzeichnen.
  Unter Berücksichtigung der Identität von $\log_{0,5} (. . .) ≙ \log_{\frac{1}{2}} (. . .) ≙ - \log_{2} (. . .)$
  $A_{1} : y = - 2 \cdot \log_{0,5} (- 1 + 3) + 1,5 = - 2 \cdot (- \log_{2} (2) + 1,5 = - 2 \cdot (- 1) + 1,5 = 3,5$
  $A_{2} : y = - 2 \cdot \log_{0,5} (3 + 3) + 1,5 = - 2 \cdot (- \log_{2} (6) + 1 = - 2 \cdot (- 2,58) + 1,5 = 6,66$
  $C_{1} : y = 2 \cdot \log_{0,5} (- 1 + 4) + 3,5 = 2 \cdot (- \log_{2} (3) + 3,5 = 2 \cdot (- 1,58) + 3,5 = 0,34$
  $C_{2} : y = 2 \cdot \log_{0,5} (3 + 4) + 3,5 = 2 \cdot (- \log_{2} (7) + 3,5 = 2 \cdot (- 2,81) + 3,5 = - 2,12$
  $\Rightarrow$ $𝐀_{𝟏} (- 𝟏 │ 𝟑,𝟓) 𝐂_{𝟏} (- 𝟏 │ 𝟎,𝟑𝟒) 𝐀_{𝟐} (𝟑 | 𝟔,𝟔𝟔) 𝐂_{𝟐} (𝟑 │ - 𝟐,𝟏𝟐)$
  Diagonalen $A_{1} C_{1} = e$ und $A_{2} C_{2} = f$ einzeichnen.
  2. Eckpunkte $B_{1}, B_{2}$ sowie $D_{1}, D_{2}$ berechnen und einzeichnen:
  aus Vektor $\vec{A_{n} B_{n}} = (\begin{array}{c} - 2 \\ - 2,5 \end{array})$ ergeben sich die $x -$ und $y -$ Komponenten für die Abstandsverhältnisse der Punkte $B_{n} = - 2 L E$ Abstand von Diagonale $f$ und $- 2,5 L E$ Abstand von $A_{n}$ , siehe nachfolgende Zeichnung.
  Damit ergeben sich die Koordinaten von $B_{n}$ und $D_{n}$ wie folgt:
  aus $A_{1} (- 1 | 3,5) : \Rightarrow B_{1} (- 1 - 2 │ 3,5 - 2,5) \Rightarrow B_{1} (- 3 │ 1)$
  aus $A_{2} (3 | 6,66) : \Rightarrow B_{2} (3 - 2 | 6,66 - 2,5) \Rightarrow B_{2} (1 | 4,16)$
  $D_{n}$ liegen spiegelbildlich zu $B_{n}$ , d.h. $x -$ Komponenten der $B_{n}$ werden mit $(2 + 2) = + 4 L E$ berechnet:
  aus $B_{1} (- 3 │ 1) : \Rightarrow D_{1} (- 3 + 4 │ 1) \Rightarrow D_{1} (1 │ 1)$
  aus $B_{2} (1 | 4,16) : \Rightarrow D_{2} (1 + 4 | 4,16) \Rightarrow D_{2} (5 | 4,16)$
  Graphen $f_{1}$ und $f_{2}$ gezeichnet mit https://www.mathway.com,
  Drachenvierecke $A_{1} B_{1} C_{1} D_{1}$ und $A_{2} B_{2} C_{2} D_{2}$ mit den zuvor berechneten Werten einzeichnen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Eckpunkte $A_{1}$ und $C_{1}$ sowie $A_{2}$ und $C_{2}$ der Drachenvierecke berechnen und ins KOSY einzeichnen;
  Eckpunkte $B_{1}$ und $B_{2}$ sowie $D_{1}$ und $D_{2}$ der Drachenvierecke berechnen und ins KOSY einzeichenen
4. Zeigen Sie rechnerisch, dass für die Länge der Strecken $A_{n} C_{n}$ in Abhängigkeit von der Abszisse $x$ der Punkte $A_{n}$ gilt: $| A_{n} C_{n} | (x) = [- 2 \cdot \log_{0,5} (x^{2} + 7 x + 12) - 2] LE$ . (2 P)
  
  geg.: Punkte $A_{n}$ auf $f_{1} : y = - 2 \cdot \log_{0,5} (x + 3) + 1,5$ ;
  Punkte $C_{n}$ auf $f_{2} : y = 2 \cdot \log_{0,5} (x + 4) + 3,5$ ;
  ges.: $| A_{n} C_{n} | (x)$
  Ansatz und Rechnung:
  $| A_{n} C_{n} | = f_{1} (x) - f_{2} (x)$
  $| A_{n} C_{n} | (x) = [- 2 \cdot \log_{0,5} (x + 3) + 1,5] - [2 \cdot \log_{0,5} (x + 4) + 3,5]$
  $| A_{n} C_{n} | (x) = - 2 \cdot \log_{0,5} (x + 3) + 1,5 - 2 \cdot \log_{0,5} (x + 4) - 3,5$
  $| A_{n} C_{n} | (x) = - 2 \cdot \log_{0,5} (x + 3) - 2 \cdot \log_{0,5} (x + 4) - 2$
  $| A_{n} C_{n} | (x) = - 2 \cdot [\log_{0,5} (x + 3) + \log_{0,5} (x + 4)] - 2$
  mit 1. Logarithmusgesetz: $\log_{a} (x) + \log_{a} (y) = \log_{a} (x \cdot y)$ folgt:
  $| A_{n} C_{n} | (x) = - 2 \cdot \log_{0,5} [(x + 3) \cdot (x + 4)] - 2$
  $| 𝐀_{𝐧} 𝐂_{𝐧} | (𝐱) = - 𝟐 \cdot \log_{𝟎,𝟓} (𝐱^{𝟐} + 𝟕 𝐱 + 𝟏𝟐) - 𝟐 L E x \in ℝ; x > - 1,26$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechnung der Strecke $| A_{n} C_{n} | (x)$
5. Das Drachenviereck $A_{3} B_{3} C_{3} D_{3}$ ist eine Raute.
  Berechnen Sie die x-Koordinate des Punktes $A_{3}$ . (3 P)
  
  geg.: Drachenviereck $A_{3} B_{3} C_{3} D_{3}$ wird Raute
  ges.: $x -$ Koordinate von Punkt $A_{3} (x | y)$
  Ansatz und Rechnung:
  Bei einer Raute halbieren sich die Diagonalen. Die Entfernung von $A_{3}$ zum Schnittpunkt $M$ beträgt $2,5 L E$ .
  Daher ist $| A_{3} C_{3} | = 2 \cdot 2,5 L E$ .
  siehe Daten aus Aufgabe B_3c und B_3d
  $\begin{array}{l} \Rightarrow - 2 \cdot \log_{0,5} (x^{2} + 7 x + 12) - 2 ≙ 2 \cdot 2,5 L E x \in ℝ; x > - 1,26 \end{array}$ $\Rightarrow - 2 \cdot \log_{0,5} (x^{2} + 7 x + 12) - 2 = 5$ | $: (- 2)$
  $\Rightarrow \log_{0,5} (x^{2} + 7 x + 12) + 1 = - 2,5$ | $+ 2,5$
  Anwendung der Identität von $\log_{\frac{1}{a}} (x) ≙ - \log_{a} (x)$
  $\Rightarrow - \log_{2} (x^{2} + 7 x + 12) + 3,5 = 0$ | $\cdot (- 1)$
  $\Rightarrow \log_{2} (x^{2} + 7 x + 12) - 3,5 = 0$ | Logarithmus in Potenz umwandeln
  $\begin{array}{l} x = \log_{a} (y) \Leftrightarrow y = a^{x} \end{array}$ $\Rightarrow x^{2} + 7 x + 12 - 2^{3,5} = 0$ | Potenz ausrechnen
  $\Rightarrow x^{2} + 7 x + 12 = 11,31$ | $- 11,31$
  $\begin{array}{l} \Rightarrow 𝐱^{𝟐} + 𝟕 𝐱 + 𝟎,𝟔𝟗 = 𝟎 \end{array}$
  a-b-c-Formel ("Mitternachtsformel") anwenden: $x_{1,2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
  1. Diskriminante berechnen mit $a = 1$ , $b = 7$ , $c = 0,69$ :
  $𝐃 = 𝐛^{𝟐} - 𝟒 \cdot 𝐚 \cdot 𝐜 = 7^{2} - 4 \cdot 1 \cdot 0,69 = 49 - 2,76 = 46,24$
  $\Rightarrow 𝐃 > 𝟎 \Leftrightarrow$ 2 Lösungen
  2. D in a-b-c-Formel einsetzen:
  $x_{1,2} = \frac{- b \pm \sqrt{D}}{2 a} = \frac{- 7 \pm \sqrt{46,24}}{2} = \frac{- 7 \pm 6,8}{2}$
  $\Rightarrow x_{1} = \frac{- 7 + 6,8}{2} = - \frac{0,2}{2} = - 0,1$
  $\Rightarrow x_{2} = \frac{- 7 - 6,8}{2} = - \frac{13,8}{2} = - 6,9$ Wegen $x > - 1,26$ fällt diese Lösung weg.
  Die $x$ -Koordinate von $A_{3}$ ist also $- 0,1$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechnung der x-Koordinate eines Punktes mithilfe a-b-c-Formel
6. Bestätigen Sie durch Rechnung, dass für die Gleichung des Trägergraphen $t$ der
  Punkte $B_{n}$ gilt: $y = - 2 \cdot \log_{0,5} (x + 5) - 1$ mit $x, y \in ℝ$ .
  Geben Sie sodann die Gleichung des Trägergraphen $k$ der Punkte $D_{n}$ an. (3 P)
  
  geg.: Zur Berechnung der Punkte $B_{n}$ werden die $x -$ und $y -$ Komponenten der Gleichungen $f_{1}$ und $f_{2}$ jeweils mit den Koordinaten von $\vec{A_{n} B_{n}} = (\begin{array}{c} - 2 \\ - 2,5 \end{array})$ ergänzt.
  Abstand der Punkte $A_{n}$ zu $B_{n}$ ist $- 2 L E$ ;
  Abstand der Punkte $A_{n}$ zu Diagonale $f$ ist $- 2,5 L E$
  Die Punkte $D_{n}$ liegen spiegelbildlich zur Ordinatenachse, also $+ 2 L E$ von Diagonale $f$ und $- 2,5 L E$ von den Punkten $A_{n}$
  ges.: Trägergraph $t$ für Punkte $B_{n}$ und Trägergraph $k$ für Punkte $D n$ .
  Ansatz und Rechnung:
  1. Berechnung $t$ von $B_{n}$ mithilfe von
  $f_{1}$ : $y = - 2 \cdot \log_{0,5} (x + 3) + 1,5$ und $\vec{𝐀_{𝐧} 𝐁_{𝐧}} = (\begin{array}{c} - 𝟐 \\ - 𝟐,𝟓 \end{array})$
  $x_{B_{n}} = x - 2 \Rightarrow x = x_{B_{n}} + 2$
  $\land y_{B_{n}} = - 2 \cdot \log_{0,5} (x + 3) + 1,5 - 2,5 x_{B n}, y_{B n}, x \in ℝ; x > - 1,26$
  $x$ in $y_{B_{n}}$ einsetzen:
  $y_{B_{n}} = - 2 \cdot \log_{0,5} (x_{B_{n}} + 2 + 3) + 1,5 - 2,5$
  $y_{B_{n}} = - 2 \cdot \log_{0,5} (x_{B_{n}} + 5) - 1 x_{B_{n}}, y_{B_{n}} \in ℝ$
  $\begin{array}{l} \Rightarrow 𝐭 : 𝐲 = - 𝟐 \cdot \log_{𝟎,𝟓} (𝐱 + 𝟓) - 𝟏 x, y \in ℝ \end{array}$
  2. Berechnung $k$ von $D_{n}$ mithilfe von
  $f_{1}$ : $y = - 2 \cdot \log_{0,5} (x + 3) + 1,5$ und $\vec{𝐀_{𝐧} 𝐃_{𝐧}} = (\begin{array}{c} 𝟐 \\ - 𝟐,𝟓 \end{array})$
  $x_{D n} = x + 2 \Rightarrow x = x_{D n} - 2$
  $\land y_{D n} = - 2 \cdot \log_{0,5} (x + 3) + 1,5 - 2,5 x_{B n}, y_{B n}, x \in ℝ; x > - 1,26$
  $x$ in $y_{D_{n}}$ einsetzen:
  $y_{D_{n}} = - 2 \cdot \log_{0,5} (x_{D_{n}} - 2 + 3) + 1,5 - 2,5$
  $y_{D_{n}} = - 2 \cdot \log_{0,5} (x_{D_{n}} + 1) - 1 x_{B_{n}}, y_{B_{n}} \in ℝ$
  $\Rightarrow 𝐤 : 𝐲 = - 𝟐 \cdot \log_{𝟎,𝟓} (𝐱 + 𝟏) - 𝟏 x, y \in ℝ$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Trägergraphen $t$ und $k$ für Punkte $B_{n}$ und $D_{n}$ berechnen
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe B4
Der Punkt $A (0 | - 4)$ legt mit den Pfeilen $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ und $\vec{A D_{n}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$ für
$φ \in [0^{\circ}; 90^{\circ}]$ Parallelogramme $A B C_{n} D_{n}$ fest.
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
1. Berechnen Sie die Koordinaten der Pfeile $\vec{A D_{1}}$ für $φ = 30^{\circ}$ und $\vec{A D_{2}}$ für $φ = 60^{\circ}$ .
  Zeichnen Sie sodann die Parallelogramme $A B C_{1} D_{1}$ und $A B C_{2} D_{2}$ in ein Koordinatensystem ein. (4 P)
  Für die Zeichnung: Längeneinheit $1 cm$ ; $- 3 \leq x \leq 5; - 4 \leq y \leq 6$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektorrechnung
  geg.: $A (0 | - 4)$ , Vektor $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ ; $\vec{A D_{n}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$ für $φ \in [0 °; 90 °]$
  ges.: Parallelogramme $A B C_{n} D_{n}$ : $A B C_{1} D_{1}$ und $A B C_{2} D_{2}$
  Ansatz und Rechnung:
  Benutze dabei $\sin 30^{\circ} = \frac{1}{2} = 0,5$ und $\sin 60^{\circ} = \sqrt{\frac{3}{4}} \approx 0,87$
  1. Berechnung $\vec{A D_{1}} (für φ = 30 °)$ und $\vec{A D_{2}} (für φ = 60 °)$ :
  $\vec{A D_{1}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin 30 ° \\ 9 - 10 \cdot \sin^{2} 30 ° \end{array}) = (\begin{array}{c} 3 - 6 \cdot 0,5 \\ 9 - 10 \cdot {0,5}^{2} \end{array}) = (\begin{array}{c} 3 - 3 \\ 9 - 10 \cdot 0,25 \end{array}) = (\begin{array}{c} 0 \\ 9 - 2,5 \end{array}) = (\begin{array}{c} 0 \\ 6,5 \end{array})$
  $\vec{A D_{2}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin 60 ° \\ 9 - 10 \cdot \sin^{2} 60 ° \end{array}) = (\begin{array}{c} 3 - 6 \cdot 0,87 \\ 9 - 10 \cdot {0,87}^{2} \end{array}) = (\begin{array}{c} 3 - 5,2 \\ 9 - 10 \cdot 0,75 \end{array}) = (\begin{array}{c} - 2,2 \\ 9 - 7,5 \end{array}) = (\begin{array}{c} - 2,2 \\ 1,5 \end{array})$
  2. Zeichnung: $L E = 1 c m$ ; mit $x : - 3 ≦ x ≦ 5$ und $y : - 4 ≦ y ≦ 6$ ,
  mit $A (0 | - 4)$ , $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ , $\vec{A D_{1}} = (\begin{array}{c} 0 \\ 6,5 \end{array})$ und $\vec{A D_{2}} = (\begin{array}{c} - 2,2 \\ 1,5 \end{array})$ Parallelogramme $A B C_{1} D_{1}$ und $A B C_{2} D_{2}$ zeichnen:
  Parallelogramme $A B C_{1} D_{1}$ und $A B C_{2} D_{2}$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechnung der Vektoren $\vec{A D_{1}} (für φ = 30 °)$ und
2. Berechnen Sie das Maß des Winkels $B A D_{1}$ . (1,5 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Trigonometrie, Tangens
  geg.: Strecke $X A = 3 L E$ , $X B = 4 L E$
  ges.: $∢ B A D_{1}$ , siehe Zeichnung Aufgabe 4a
  Ansatz und Rechnung:
  $∢ B A D_{1} ≙ ∢ B A X = \tan \frac{𝐆 𝐊}{𝐀 𝐊} = \frac{4}{3} = 1, 3$
  $\Rightarrow ∢ 𝐁 𝐀 𝐃_{𝟏} = 𝟓𝟑,𝟏𝟑 °$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Winkel $B A D_{1}$ ist derselbe wie der Winkel $B A X$ mit $X (0 | - 1)$ .
  Berechne den Tangens dieses Winkels.
3. Zeigen Sie rechnerisch, dass für die Koordinaten der Punkte $C_{n}$ in Abhängigkeit
  von $φ$ gilt: $C_{n} (7 - 6 \cdot \sin φ | 8 - 10 \cdot \sin^{2} φ)$ . (1,5 P)
  
  geg.: $A (0 | - 4)$ , $O (0 | 0)$ $\Rightarrow$ $\vec{O A} = (\begin{array}{c} 0 - 0 \\ - 4 - 0 \end{array}) = (\begin{array}{c} 0 \\ - 4 \end{array})$ ; $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ ;
  $\vec{A D_{n}} = (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$ $= \vec{B C_{n}}$
  ges.: Koordinaten der Punkte $C_{n} (φ)$
  Ansatz und Rechnung:
  Berechnung mithilfe Vektoraddition $\vec{O C_{n}} = \vec{O A} \oplus︎ \vec{A B} \oplus︎ \vec{B C_{n}}$ mit $φ \in [0 °; 90 °]$
  $\Rightarrow \vec{O C_{n}} (φ) = (\begin{array}{c} 0 \\ - 4 \end{array}) \oplus︎ (\begin{array}{c} 4 \\ 3 \end{array}) \oplus︎ (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$ mit $φ \in [0 °; 90 °]$
  $\Rightarrow \vec{𝐎 𝐂_{𝐧}} (𝛗) = (\begin{array}{c} 𝟕 - 𝟔 \cdot \sin 𝛗 \\ 𝟖 - 𝟏𝟎 \cdot \sin^{𝟐} 𝛗 \end{array})$
  somit ist $𝐂_{𝐧} (𝟕 - 𝟔 \cdot \sin 𝛗 | 𝟖 - 𝟏𝟎 \cdot \sin^{𝟐} 𝛗)$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechnung Vektor $\vec{O C_{n}} (φ)$ und damit die Koordinaten von $C_{n} (φ)$
4. Der Punkt $C_{3}$ des Parallelogramms $A B C_{3} D_{3}$ liegt auf der $x$ -Achse.
  Berechnen Sie die $x$ -Koordinate des Punktes $C_{3}$ . (2,5 P)
  
  geg.: $𝐂_{𝐧} (𝟕 - 𝟔 \cdot 𝐬 𝐢 𝐧 𝛗 | 𝟖 - 𝟏𝟎 \cdot 𝐬 𝐢 𝐧^{𝟐} 𝛗)$
  ges.: $x$ für $C_{3}$ auf der $x$ -Achse
  Ansatz und Rechnung:
  wenn $C_{3}$ auf der $x$ -Achse liegt, dann ist die $y$ -Koordinate $= 0$
  $\Rightarrow y : 8 - 10 \cdot \sin^{2} φ = 0 mit φ \in [0 °; 90 °]$
  $8 = 10 \cdot \sin^{2} φ | : 10$
  $\frac{8}{10} = \sin^{2} φ | \sqrt{}$
  $\sqrt{0,8} = \sqrt{\sin^{2} φ} \Rightarrow 0,8944 = \sin φ \Rightarrow φ ≙ 63,43 °$
  Berechnung der $x$ -Koordinate durch Einsetzen von $\sin φ = 0,8944$ :
  $\Rightarrow 𝐱_{𝐂_{𝟑}} = 77 - 6 \cdot 0,8944 = 7 - 5,37 = 𝟏,𝟔𝟑$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Punkte auf der $x$ -Achse haben die y-Koordinate Null. Berechne daraus $\sin φ$ und damit $x$ .
5. Das Parallelogramm $A B C_{4} D_{4}$ ist ein Rechteck.
  Berechnen Sie den zugehörigen Wert für $φ$ . (3,5 P)
  
  geg.: $A (0 | - 4)$ ; $\vec{A B} = (\begin{array}{c} 4 \\ 3 \end{array})$ ; $\vec{A D_{n}} (φ) = (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array})$
  ges.: $φ$ unter der Bedingung, dass $A B C_{4} D_{4}$ Rechteck ist
  Ansatz und Rechnung:
  Bedingung für $A B C_{4} D_{4}$ ≙ Rechteck $\Rightarrow$ Skalarprodukt $\vec{A B} ⊙ \vec{A D_{n}} = 0$ :
  $(\begin{array}{c} 4 \\ 3 \end{array}) ⊙ (\begin{array}{c} 3 - 6 \cdot \sin φ \\ 9 - 10 \cdot \sin^{2} φ \end{array}) = 0$ mit $φ \in [0 °; 90 °]$
  Formel für Berechnung Skalarprodukt: $\vec{a} ⊙ \vec{b} = (\begin{array}{c} a_{x} \\ a_{y} \end{array}) ⊙ (\begin{array}{c} b_{x} \\ b_{y} \end{array}) = a_{x} \cdot b_{x} + a_{y} \cdot b_{y}$
  $\Rightarrow 𝟒 \cdot (𝟑 - 𝟔 \cdot \sin 𝛗) + 𝟑 \cdot (𝟗 - 𝟏𝟎 \cdot \sin^{𝟐} 𝛗) = 𝟎 |$ ausmultiplizieren
  $12 - 24 \cdot \sin φ + 27 - 30 \cdot \sin^{2} φ = 0 |$ zusammenfassen
  $39 - 24 \cdot \sin φ - 30 \cdot \sin^{2} φ = 0 |$ :30
  $1,3 - 0,8 \cdot \sin φ - \sin^{2} φ = 0 |$ umschreiben in quadratische Gleichung
  $- \sin^{𝟐} 𝛗 - 𝟎,𝟖 \cdot \sin 𝛗 + 𝟏,𝟑 = 𝟎$
  Lösung mithilfe der a-b-c-Formel:
  1. Berechnung der Determinante $D$ mit $a = - 1$ ; $b = - 0,8$ ; $c = 1,3$
  $\Rightarrow 𝐃 = 𝐛^{𝟐} - 𝟒 \cdot 𝐚 \cdot 𝐜 = (- 0,8)^{2} - 4 \cdot (- 1) \cdot (1,3) = 0,64 + 5,2 = 5,84$
  $\Rightarrow D > 0 \leftrightarrow$ 2 Lösungen
  2. $D$ in a-b-c-Formel einsetzen:
  $\Rightarrow \sin 𝛗_{𝟏,𝟐} = \frac{- b \pm \sqrt{D}}{2 a} = \frac{- (- 0,8) \pm \sqrt{5,84}}{2 \cdot (- 1)} = \frac{𝟎,𝟖 \pm 𝟐,𝟒𝟏𝟔𝟔}{- 𝟐}$
  $\to \sin φ_{1} = \frac{0,8 + 2,4166}{- 2} = \frac{3,2166}{- 2} = - 1,6083$ nicht definiert!
  $\to \sin 𝛗_{𝟐} = \frac{𝟎,𝟖 - 𝟐,𝟒𝟏𝟔𝟔}{- 𝟐} = \frac{- 𝟏,𝟔𝟏𝟔𝟔}{- 𝟐} = 𝟎,𝟖𝟎𝟖𝟑$
  $\Rightarrow 𝛗_{𝟐} = 𝟓𝟑,𝟗𝟑 ° \to φ \in [0 °; 90 °]$
  $\Rightarrow 𝕃 = [𝟓𝟑,𝟗𝟑 °]$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Berechnung Skalarprodukt mit $\vec{A B}$ und $\vec{A D_{n}} (φ)$ ,
  Lösung der trigonometrischen Gleichung mit a-b-c-Formel
6. Begründen Sie, weshalb für die y-Koordinate aller Punkte $C_{n}$ gilt: $y_{C_{n}} \geq - 2$ . (1,5 P)
  
  geg.: $\vec{O C_{n}} (φ) = (\begin{array}{c} 7 - 6 \cdot \sin φ \\ 8 - 10 \cdot \sin^{2} φ \end{array})$
  ges.: Nachweis, dass für $y -$ Koordinate aller Punkte $C_{n}$ gilt: $\begin{array}{l} 𝐲_{𝐜_{𝐧}} ≧ - 𝟐 \end{array}$
  Ansatz und Rechnung:
  $𝐲_{𝐂_{𝐧}} = 𝟖 - 𝟏𝟎 \cdot \underset{⏟}{\sin^{𝟐} 𝛗} ≧ - 𝟐$
  $\underset{⏟}{\sin^{2} φ ≦ 1}$
  $10 \cdot 1 ≦ 10$
  $\Rightarrow 𝐲_{𝐜_{𝐧}} ≧ 𝟖 - 𝟏𝟎 ≧ - 𝟐$ q.e.d.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Benutze, dass $\sin^{2} φ \leq 1$ ist.