Nachtermin Teil A - lernen mit Serlo!

Der Punkt $A (1,5 ∣ - 1)$ legt zusammen mit Punkten

$B_n(\sin\varphi-3|4\cdot\cos^2\varphi-1)$ für $\varphi\in [0°; 360°]$ Pfeile $\overrightarrow{AB_n}$ fest.

Runden Sie im Folgenden auf eine Stelle nach dem Komma.

Im Koordinatensystem ist der Pfeil $\overrightarrow{AB_1}= \begin{pmatrix} -3{,}5 \\ 0 \end{pmatrix}$
eingezeichnet. Bestimmen Sie den zugehörigen Wert von $\varphi$ .

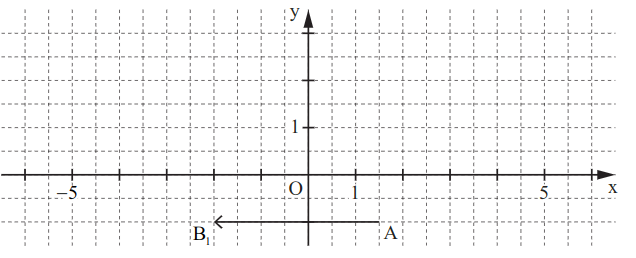
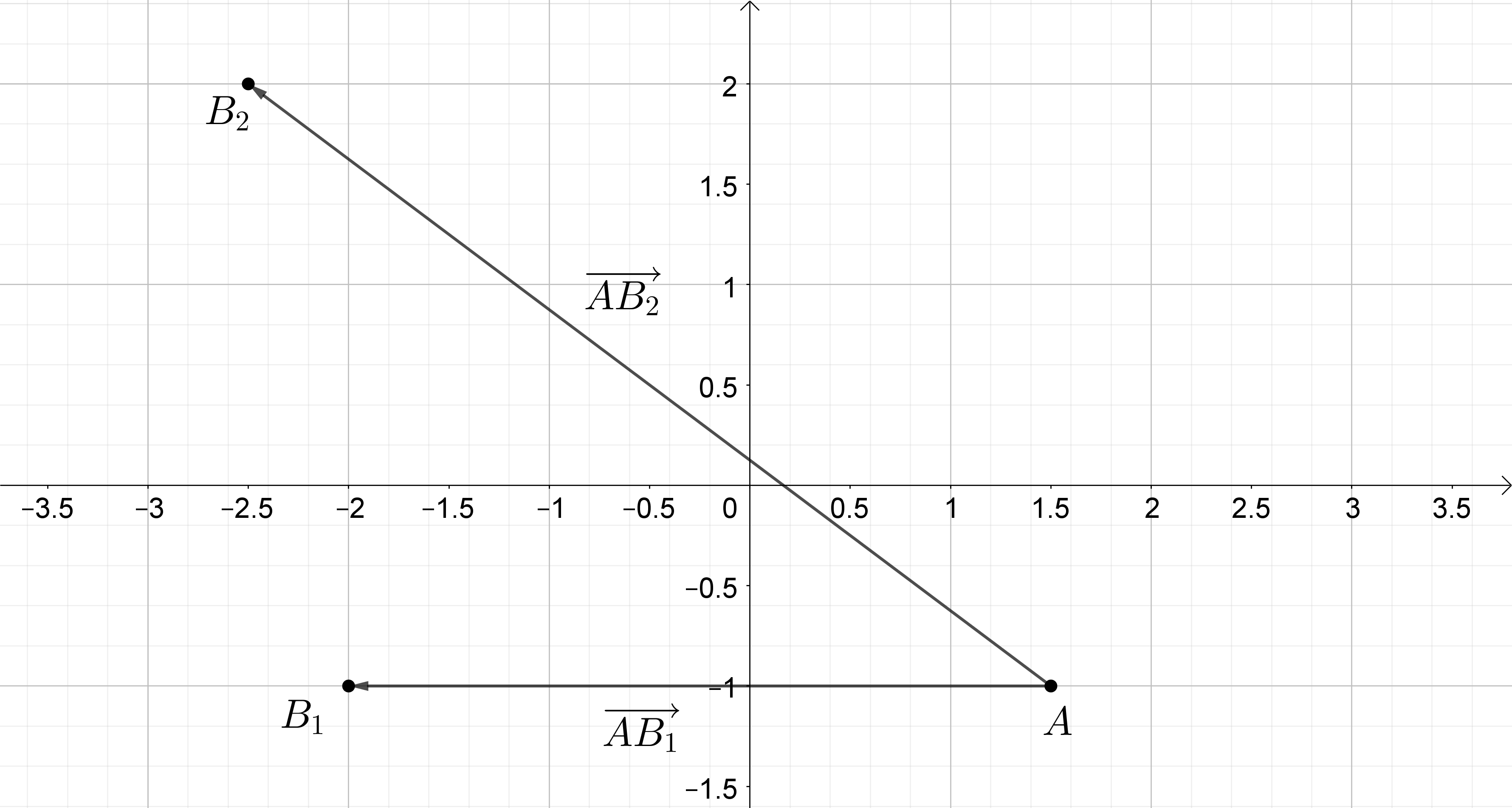
Um diese Aufgabe zu lösen, berechnet man zunächst mithilfe der angegebenen Punkte $A$ und $B_{n}$ den allgemeinen Vektor $\overrightarrow{AB_n}$ . Es gilt:
$\displaystyle \def\arraystretch{1.25} \begin{array}{c} \overrightarrow{AB_n} = \overrightarrow{OB_n} - \overrightarrow{OA} &=& \begin{pmatrix} \sin \varphi - 3 \\ 4\cdot \cos^2\varphi -1 \end{pmatrix} - \begin{pmatrix} 1{,}5 \\ -1 \end{pmatrix} \\ \\ &=& \begin{pmatrix} \sin \varphi - 3 - 1{,}5 \\ 4\cdot \cos^2\varphi -1 - (-1) \end{pmatrix} \\ \\&=& \begin{pmatrix} \sin \varphi - 4{,}5 \\ 4\cdot \cos^2\varphi\end{pmatrix}. \end{array}$
Um den zum Vektor $\overrightarrow{AB_1}$ zugehörigen Winkel $\varphi$ zu bestimmen, kannst du die Einträge der Vektoren $\overrightarrow{AB_1}$ und $\overrightarrow{AB_n}$ miteinander vergleichen. Daraus erhältst du das Gleichungssystem:
$\displaystyle \def\arraystretch{1.25} \begin{array}{c} \sin \varphi - 4{,}5 &=& -3{,}5 \\ 4 \cdot \cos^2 \varphi &=& 0. \end{array}$
Betrachtet man die erste Gleichung, so erhält man durch Umstellen der Gleichung den Zusammenhang
$\displaystyle \sin\varphi=1.$
Da $\varphi \in [0; 360°]$ gilt, ist aus dem Verlauf der Sinusfunktion in diesem Intervall klar, dass $\varphi = 90°$ sein muss.
Du kannst an dieser Stelle natürlich auch die Umkehrfunktion des Sinus verwenden und erhältst ebenfalls $\varphi = \sin^{-1}(1) = 90°$ .
Da $\varphi = 90°$ auch die Gleichung $4\cdot \cos^2 \varphi = 0$ erfüllt, löst das gefundene $\varphi$ unser Gleichungssystem und du bist fertig.
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeichnen Sie den Pfeil $\overrightarrow{AB_2}$ für $\varphi=150°$ in das Koordinatensystem zu Teilaufgabe a) ein.

Du kannst bei dieser Teilaufgabe das Ergebnis für den Vektor $\overrightarrow{AB_n}$ aus Teilaufgabe a) verwenden und berechnest mit $\varphi = 150°$ :
$\displaystyle \overrightarrow{AB_2} = \begin{pmatrix} \sin (150°) - 4{,}5 \\ 4\cdot \cos^2(150°)\end{pmatrix} = \begin{pmatrix} \dfrac12 - 4{,}5 \\ 4\cdot \left( -\dfrac{\sqrt{3}}{2} \right)^2\end{pmatrix} = \begin{pmatrix} -4 \\ 3\end{pmatrix}.$
Damit kannst du den Vektor in die Skizze einzeichnen:
Hast du eine Frage oder Feedback?
Kommentiere hier 👇
Zeigen Sie, dass für den Trägergraphen der Punkte $B_{n}$ gilt:
$\displaystyle y=3-4\cdot(x+3)^2; (\mathbb{G} = \mathbb{R} \times \mathbb{R}).$

Um den Trägergraphen (oft auch als Ortskurve bekannt) berechnen zu können, musst du einen Zusammenhang zwischen der $y$ -Koordinate und der $x$ -Koordinate des Punktes $B_{n}$ herstellen.
$\displaystyle \def\arraystretch{1.25} \begin{array}{rcll} x_{B_n} &=& \sin \varphi - 3&(1)\\ \wedge~y_{B_n}&=& 4\cdot \cos^2 \varphi-1&(2) \end{array}$
Aus Gleichung $(1)$ ergibt sich durch Äquivalenzumformung
$\displaystyle {\color{#009999}x_{B_n} + 3} = {\color{#009999}\sin \varphi}.$
Nun hilft dir der trigonometrische Pythagoras, das heißt die Beziehung
$\displaystyle \color{#ff6600}\cos^2 \varphi + \sin^2 \varphi = 1$
weiter, denn damit kannst du die $y$ -Koordinate wie folgt darstellen:
$\displaystyle \def\arraystretch{1.25} \begin{array}{rcl} y_{B_n} &=& 4 \cdot {\color{#ff6600}\cos^2 \varphi} - 1 \\&=& 4 \cdot ({\color{#ff6600}1 - \sin^2 \varphi})-1 \\ &=& 4 \cdot (1 - ({\color{#009999}x_{B_n}+3})^2)-1 \\&=& 4 - 4 \cdot (x_{B_n}+3)^2 - 1 \\ y_{B_n} &=& 3 - 4 \cdot (x_{B_n}+3)^2 \end{array}$
Für den Trägergraph der Punkte $B_{n}$ gilt somit
$\displaystyle y=3-4\cdot(x+3)^2$
mit $\mathbb{G} = \mathbb{R} \times \mathbb{R}$ .
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?