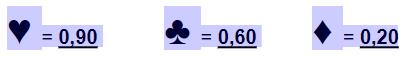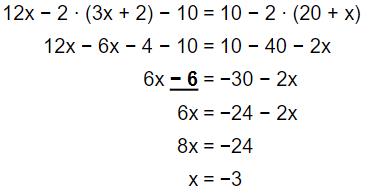Teil A

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.

(Kleine Änderungen der Formulierung aufgrund der Umwandlung in ein digitales Medium sind kursiv geschrieben.)

1
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Berechne
1. $227{,}50 : 7$
2. $516{,}2 − 83{,}75$
2
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
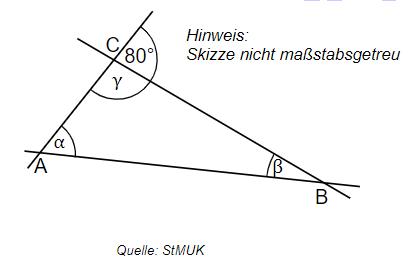
Im Dreieck $ABC$ (siehe Skizze) ist der Winkel $α$ dreimal so groß wie der Winkel $β$ . Bestimme die Größen der Winkel $α$ , $β$ und $γ$ .
3
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
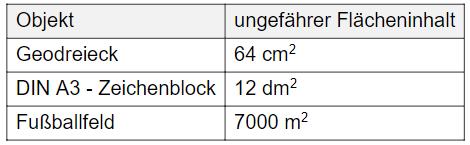
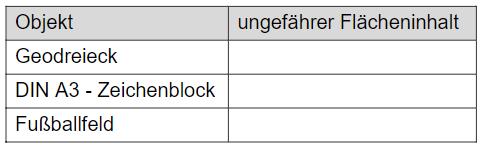
Ordne den in der linken Spalte der Tabelle genannten Objekten jeweils einen der angegebenen Flächeninhalte aus dem Kreis sinnvoll zu.
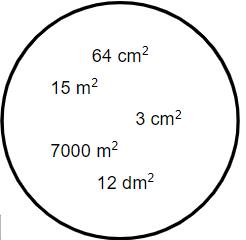
4
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Finde für jedes Symbol einen Zahlenwert, sodass jede Zeile das vorgegebene Ergebnis liefert.
5
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Kreuze die beiden Aufgaben mit dem gleichen Ergebnis an.
- $15$ % von $400$
- $30$ % von $300$
- $60$ % von $200$
- $120$ % von $100$
6
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Zu jeder Aussage passt eine der unten stehenden Grafiken. Ordne den Aussagen jeweils den Buchstaben der passenden Grafik zu. Für eine Grafik ist keine passende Aussage aufgeführt.
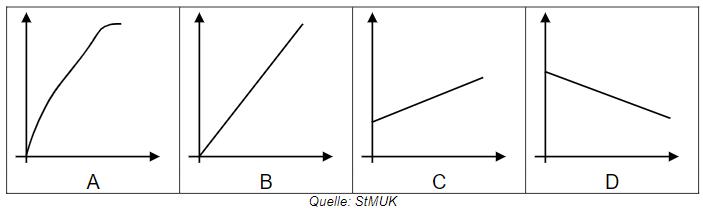
7
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
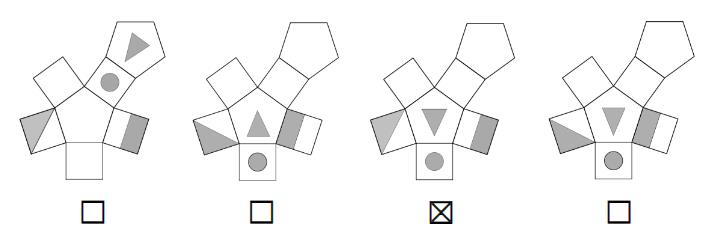
Ein Prisma hat auf vier Seiten Markierungen (siehe Skizze). Kreuze an, welches Netz zum dargestellten Körper passt.
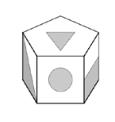
Prisma
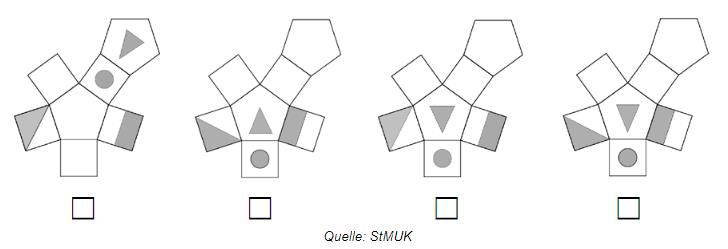
Netze

Martin hat in der folgenden Rechnung einen Fehler gemacht.

$\displaystyle 12x−2\cdot(3x+2)−10$	$=$	$\displaystyle 10−2\cdot(20+x)$
$\displaystyle 12x− 6x − 4 − 10$	$=$	$\displaystyle 10 − 40 − 2x$
$\displaystyle 6x − 6$	$=$	$\displaystyle −30 − 2x$	$\displaystyle +6$
$\displaystyle 6x$	$=$	$\displaystyle −24 − 2x$	$\displaystyle +2x$
$\displaystyle 8x$	$=$	$\displaystyle -24$
$\displaystyle x$	$=$	$\displaystyle -3$

Unterstreiche den Fehler.
Erkläre, was er falsch gemacht hat.

9
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Bei einem Würfelspiel mit einem sechsseitigen Spielwürfel wird jeweils eine Spielfigur um genauso viele Felder in Richtung des schraffierten Feldes gezogen, wie der Würfel Augen anzeigt. Es gewinnt, wer eine Spielfigur genau auf das schraffierte Feld in der Mitte ziehen kann.
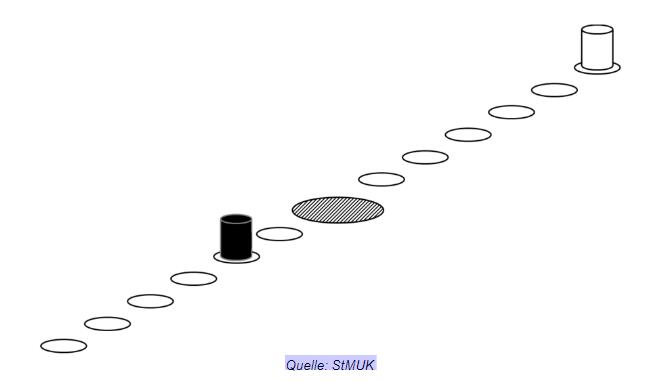
1. Gib an, mit welcher Wahrscheinlichkeit die schwarze Spielfigur beim einmaligen Würfeln das schraffierte Feld in der Mitte erreicht.
2. Umut spielt mit der weißen Spielfigur, Christine mit der schwarzen. Christine sagt: „Wenn jeder von uns einmal würfeln darf, ist die Wahrscheinlichkeit, dass ich gewinne größer. Meine Figur ist schon fast im Ziel.“ Begründe, warum Christine nicht recht hat.
10
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
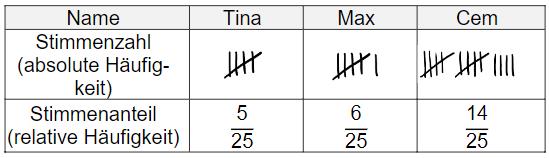
Die Klasse 9c wählt ihre Klassensprecher. Tina, Max und Cem stellen sich zur Wahl. Beim ersten Wahlgang werden die dargestellten Stimmzettel abgegeben.
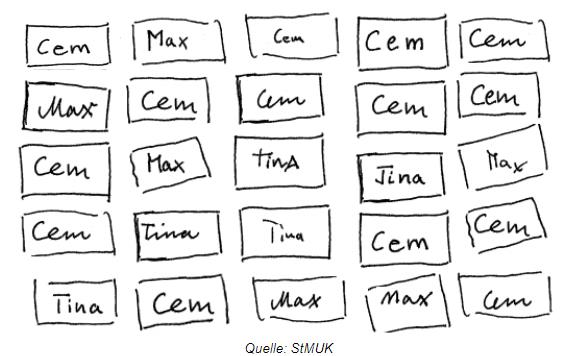
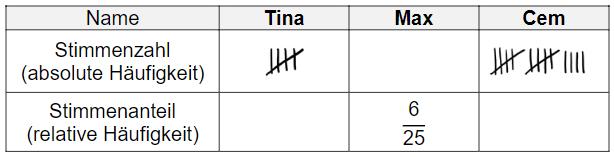
1. Erstelle mit Hilfe der Tabelle eine Übersicht über die abgegebenen Stimmen. Ergänze dazu die fehlenden Werte.
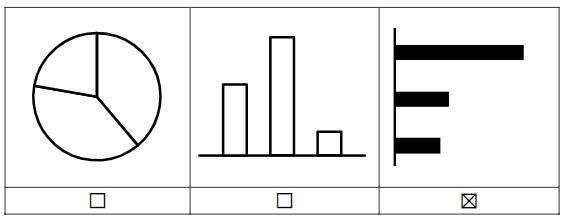
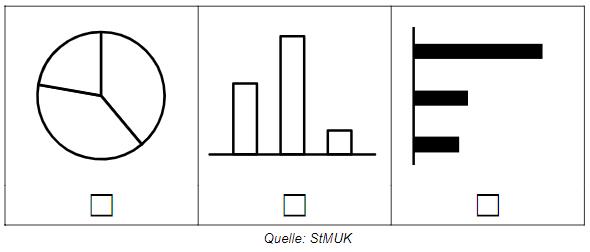
2. Nur eines der folgenden Diagramme bildet die Stimmenanteile der Klassensprecherwahl ab. Kreuze an, welches Diagramm den Sachverhalt darstellt.
11
Bayerisches Staatsministerium für Unterricht und Kultus (Gilt für: Aufgabenstellung)Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
In dem dargestellten Quader mit quadratischer Grundfläche (siehe Skizze) mit einem Volumen von $42 cm^3$ ist eine Pyramide eingefügt.
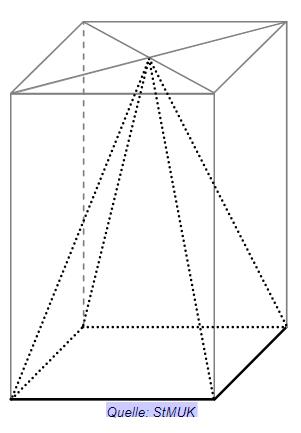
Ermittle das Volumen der Pyramide.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?