Teil A - lernen mit Serlo!

Punkte $A_n(2\cdot\sin(\varphi)-4|3\cdot\sin(\varphi)-1)$ mit $\varphi\in[0^\circ;90^\circ]$ legen zusammen mit den Punkten $B(-2|-3)$ und $D(2|3)$ Parallelogramme $A_nBC_nD$ fest.

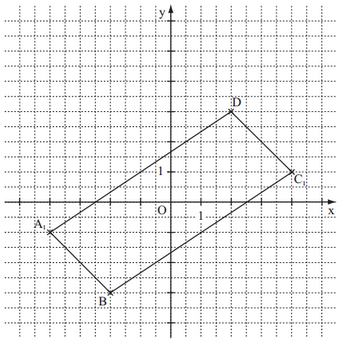
In das Koordinatensystem zur Aufgabenstellung ist das Parallelogramm $A_1BC_1D$ für $\varphi=0^\circ$ eingezeichnet.
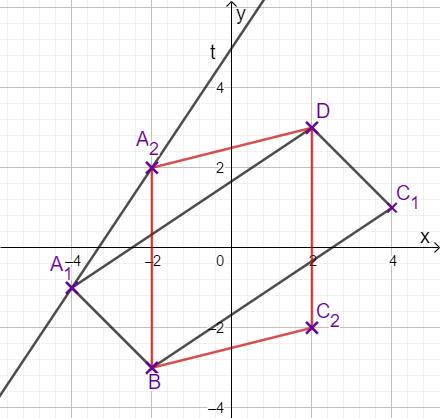
Berechnen Sie die Koordinaten des Punktes $A_2$ für $\varphi=90^\circ$ und zeichnen Sie sodann das Parallelogramm $A_2B_2C_2D$ ein.

Lösung zu Teilaufgabe a
In dieser Aufgabe beschäftigst du dich mit der Konstruktion von Parallelogrammen.
Um den Punkt $A_2$ zu berechnen, setzt du den Wert $\varphi=90°$ in $A_n(2 \cdot \sin \varphi-4|3\cdot \sin \varphi-1)$ ein und erinnerst dich, dass $\sin 90°=1$ gilt. Damit erhältst du $A_2 (-2|2)$ .
Nun kannst du den Punkt $A_2$ sowie die Verbindungsgeraden $[A_2B]$ und $[A_2D]$ in das Koordinatensystem eintragen.
Zeichne anschließend je eine Parallele zur Strecke $[A_2B]$ durch den Punkt $D$ und eine Parallele zu $[A_2D]$ durch den Punkt $B$ . Der Schnittpunkt dieser beiden Geraden liefert den Punkt $C_2$ und somit auch das Parallelogramm $A_2BC_2D$ .
Das konstruierte Parallelogramm
Hast du eine Frage oder Feedback?
Kommentiere hier 👇

Zeigen Sie rechnerisch, dass für den Trägergraphen $t$ der Punkt $A_n$ gilt:

$y=\frac32x+5\quad(\mathbb{G}=\mathbb{R}\times\mathbb{R})$ .

Zeichnen Sie den Trägergraphen $t$ in das Koordinatensystem zur Aufgabenstellung ein.

Begründen Sie, dass die Flächeninhalte $A$ aller Parallelogramme $A_nBC_nD$ maßgleich sind.

Lösung zu Teilaufgabe c

Erinnere dich an die Berechnung von Parallelogrammflächen mittels Determinante. Dies geht genauso wie im Artikel Dreiecksfläche im Koordinatensystem beschrieben; lediglich der dort erwähnte Vorfaktor $0{,}5$ fällt weg.

Du berechnest zunächst die Fläche des Dreiecks $A_nBD$ . Dazu verwendest du die Verbindungsvektoren:

$\overrightarrow{BD}=\begin{pmatrix}2-(-2)\\3-(-3)\end{pmatrix}=\begin{pmatrix}4\\6\end{pmatrix}$ und

$\displaystyle \overrightarrow{BA_n}$	$=$	$\displaystyle \begin{pmatrix}2\cdot\sin(\varphi)-4-(-2)\\3\cdot\sin(\varphi)-1-(-3)\end{pmatrix}$
	$=$	$\displaystyle \begin{pmatrix}2\cdot\sin(\varphi)-2\\3\cdot\sin(\varphi)+2\end{pmatrix}$

Nach der Determinantenformel gilt

$\displaystyle A_{\triangle A_nBD}$	$=$	$\displaystyle \frac12\cdot\left\|\overrightarrow{BD}\,\overrightarrow{BA_n}\right\|$
	$=$	$\displaystyle \frac12\cdot\begin{vmatrix}4& 2\cdot\sin(\varphi)-2\\6&3\cdot\sin(\varphi)+2\end{vmatrix}$
	$=$	$\displaystyle \frac{1}{2}\left[4\cdot (3\cdot \sin (\varphi )+2)-6\cdot (2\cdot \sin (\varphi )-2)\right]$
	$=$	$\displaystyle \frac12\left[12\cdot\sin(\varphi)+8-12\cdot\sin(\varphi)+12\right]=10\,\mathrm{(FE).}$

Aus Symmetriegründen ist der Flächeninhalt des Parallelogramms $A_nBC_nD$ das Doppelte des Dreiecksflächeninhalts:

\displaystyle A_{A_nBC_nD}=2\cdot A_{\triangle{A_nBD}}=20\,\mathrm{(FE).}

Da dieses Ergebnis unabhängig von $\varphi$ ist, folgt, dass der Flächeninhalt aller Parallelogramme konstant bleibt.

Hast du eine Frage oder Feedback?

Kommentiere hier 👇

$\displaystyle t(-4)$	$=$	$\displaystyle -1$
	↓	Setze die Definition von $t$ ein.
$\displaystyle -4\cdot m+c$	$=$	$\displaystyle -1$
	↓	Setze den Wert für $m$ ein.
$\displaystyle \displaystyle -4\cdot\frac 32+c$	$=$	$\displaystyle -1$
	↓	Vereinfache.
$\displaystyle -6+c$	$=$	$\displaystyle -1$	$\displaystyle +6$
	↓	Löse nach $c$ auf.
$\displaystyle c$	$=$	$\displaystyle 5$

Lösung zu Teilaufgabe a

Hast du eine Frage oder Feedback?

Lösung zu Teilaufgabe b

Hast du eine Frage oder Feedback?

Lösung zu Teilaufgabe c

Hast du eine Frage oder Feedback?