Aufgaben zur Achsenspiegelung und Achsensymmetrie

1
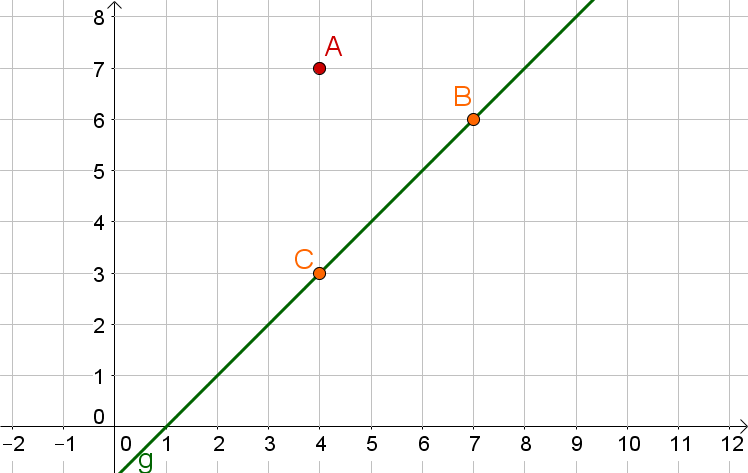
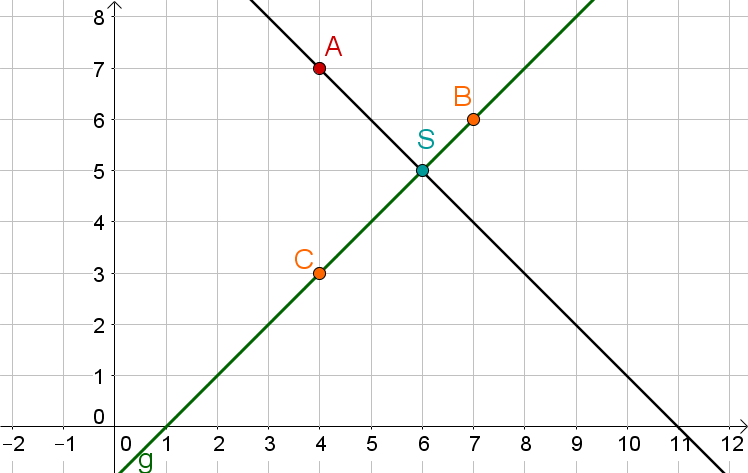
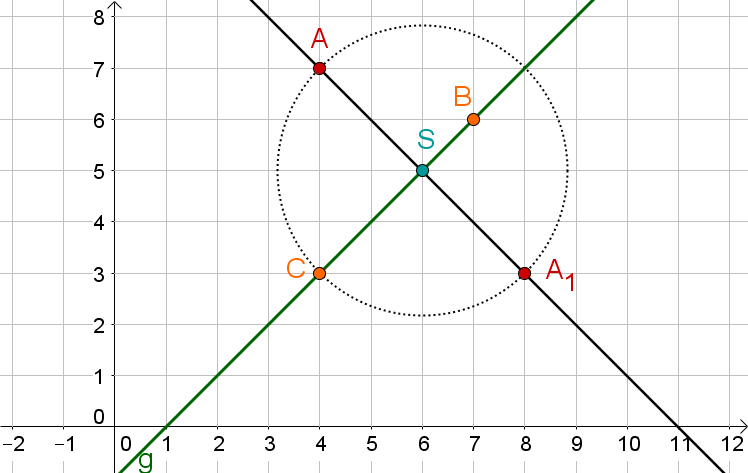
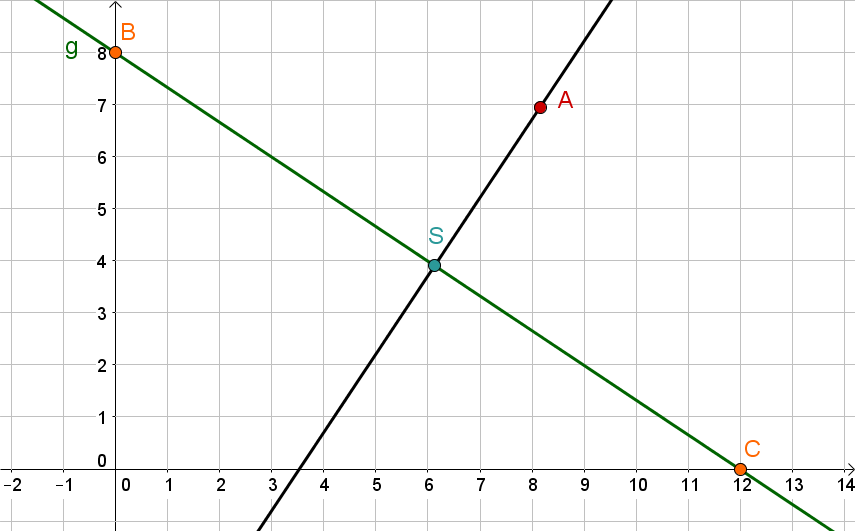
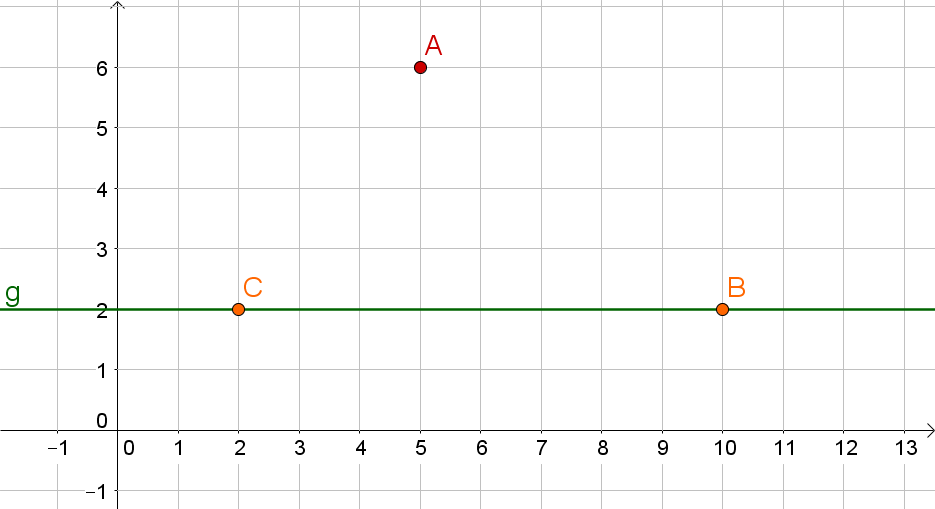
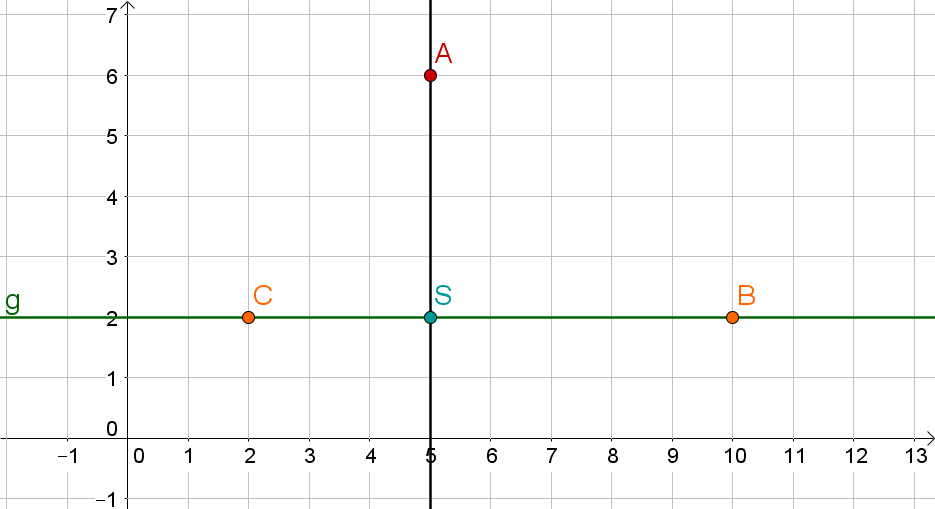
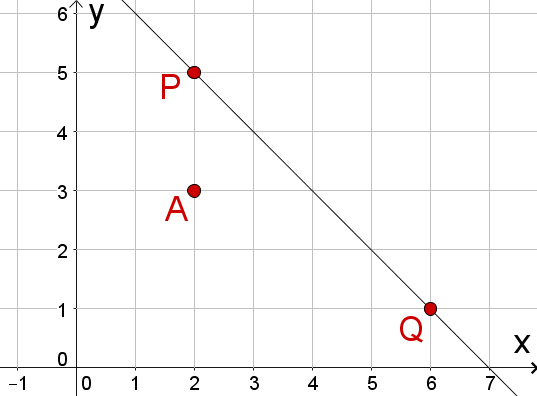
Spiegle mit Lot den gegebenen Punkt $A$ an der Gerade $g$ , welche durch die gegebenen Punkte $B$ und $C$ verläuft.
1. $A(4|7)$
  $B(7|6)$
  $C(4|3)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkte an Achsen spiegeln
  Trage als Erstes die gegebenen Punkte in ein Koordinatensystem ein. Und ziehe eine Gerade zwischen $B$ und $C$ .
  Konstruiere das Lot durch den Punkt $A$ an der Spiegelachse $g$ .
  Ziehe einen Kreis um den Mittelpunkt $S$ mit dem Radius zu $A$ . An der Stelle, an der der Kreis auf der anderen Seite von $g$ , das Lot nochmal schneidet, ist der gespiegelte Punkt von $A$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $A(8|7)$
  $B(0|8)$
  $C(12|0)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Achse spiegeln
  Trage als erstes die gegebenen Punkte in ein Koordinatensystem ein.Und zieh eine Gerade zwischen $B$ und $C$ .
  Konstruiere das Lot durch den Punkt $A$ an der Spiegelachse $g$ .
  Ziehe einen Kreis um den Schneidepunkt $S$ und dem Radius zu $A$ . An der Stelle, an der der Kreis auf der anderen Seite von $g$ , das Lot nochmal schneidet, ist der gespiegelte Punkt von $A$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $A(5|6)$
  $B(10|2)$
  $C(2|2)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Achse spiegeln
  Zeichen die gegebenen Punkte in ein Koordinatensystem ein und ziehe zwischen $B$ und $C$ die Gerade $g$ .
  Konstruiere das Lot durch den Punkt $A$ an der Spiegelachse $g$ .
  Ziehe einen Kreis um den Schneidepunkt $S$ mit dem Radius zu $A$ . An der Stelle, an der der Kreis das Lot auf der anderen Seite von $g$ nochmal schneidet, ist der gespiegelte Punkt von $A$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
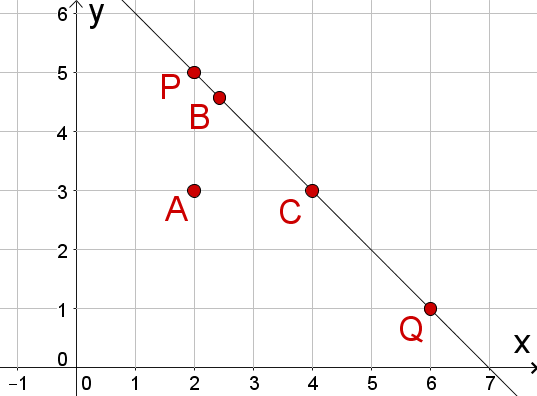
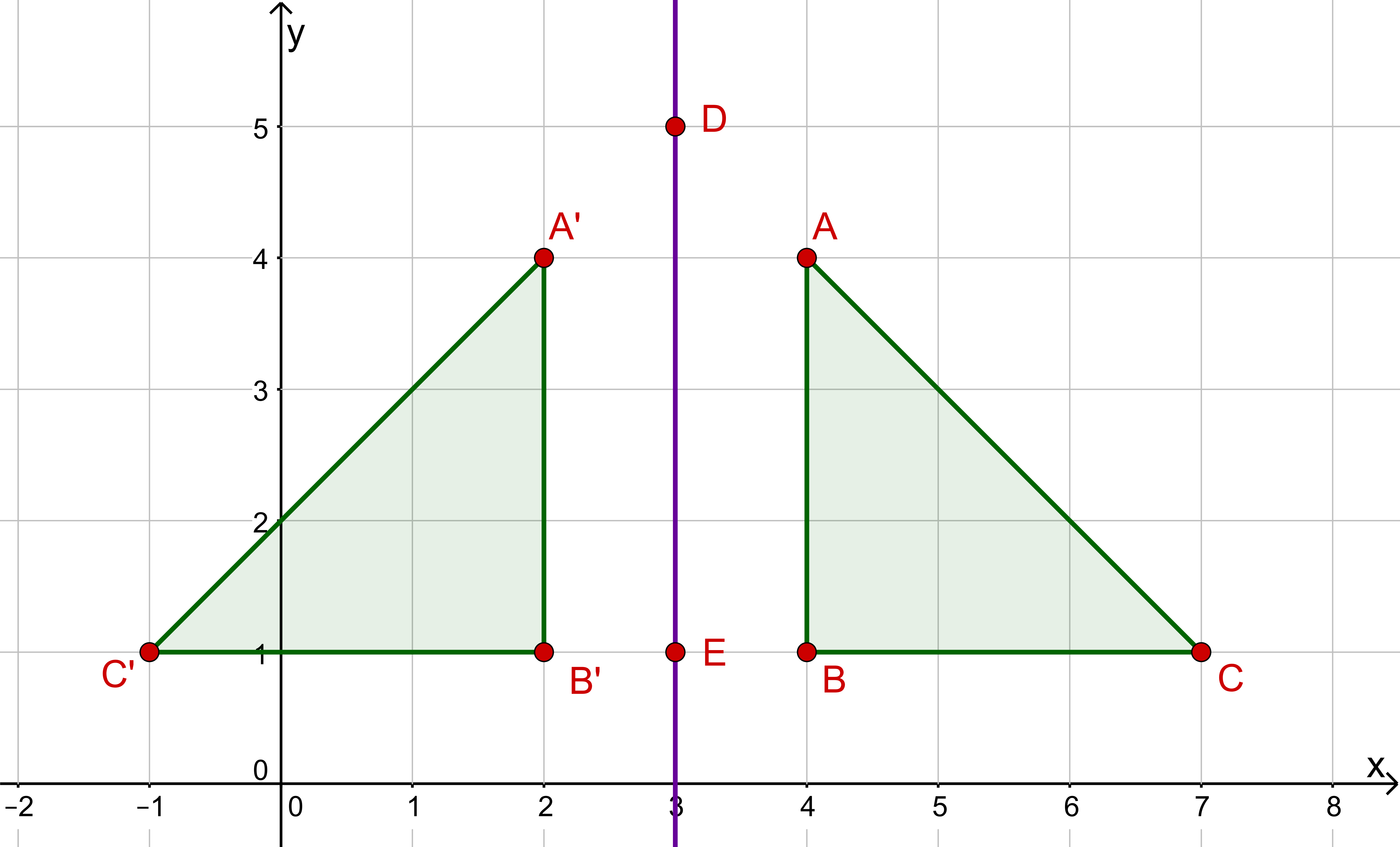
Stelle fest, ob in den folgenden Abbildungen die linke bzw. obere Figur korrekt an der Geraden $a$ gespielt wurde. Falls dies nicht der Fall, gib jeweils an, wo der Fehler liegt und welche Eigenschaften der Achsenspiegelung (Winkeltreue usw. ) verletzt sind.
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Achsenspiegelung
  Die Figur wurde nicht korrekt gespiegelt. Die Dreiecke rechts und links der Geraden sind nicht kongruent. Längen- und Winkeltreue sind verletzt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Achsenspiegelung
  Die Figur wurde nicht korrekt gespiegelt. Ein Auge der Figur ist zu weit unten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Für diese Aufgabe benötigst Du folgendes Grundwissen: Achsenspiegelung
  Die Figur wurde nicht korrekt gespiegelt. Der ursprünglich kreisförmige Kopf der Figur ist zu einer allgemeinen Ellipse geworden. Damit ist die Kreistreue verletzt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Für diese Aufgabe benötigst Du folgendes Grundwissen: Achsenspiegelung
  Die Figur wurde korrekt gespiegelt.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
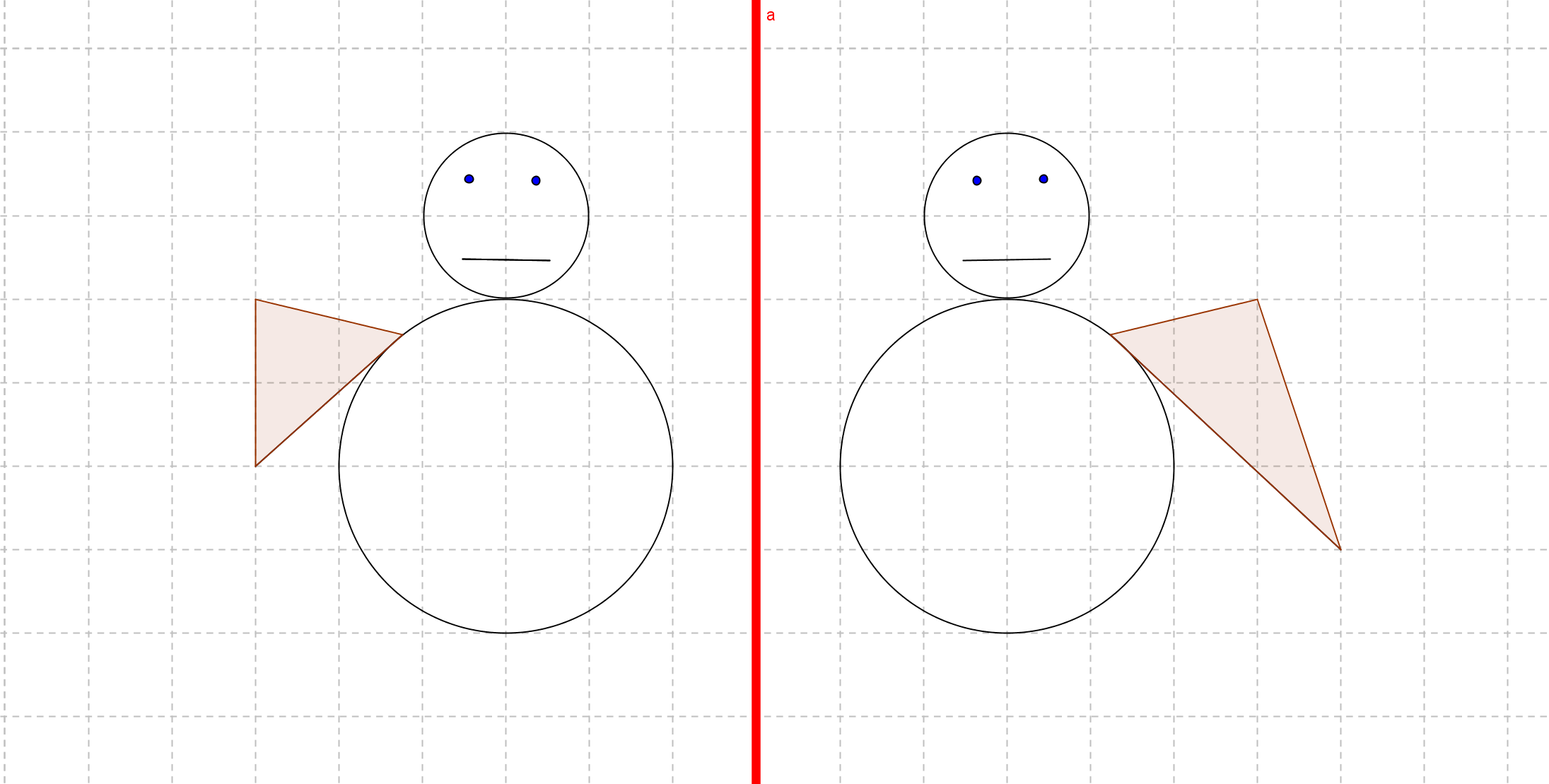
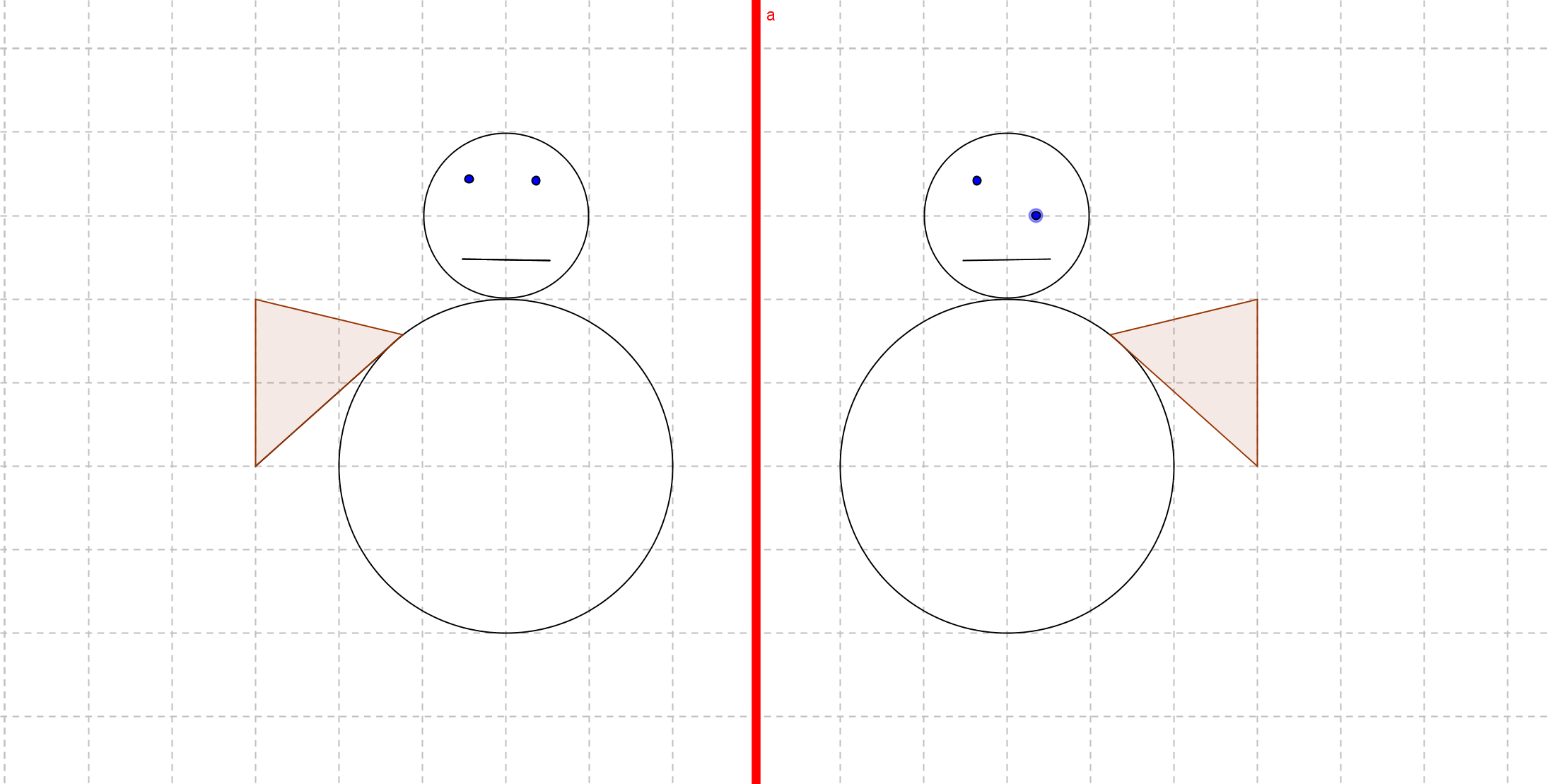
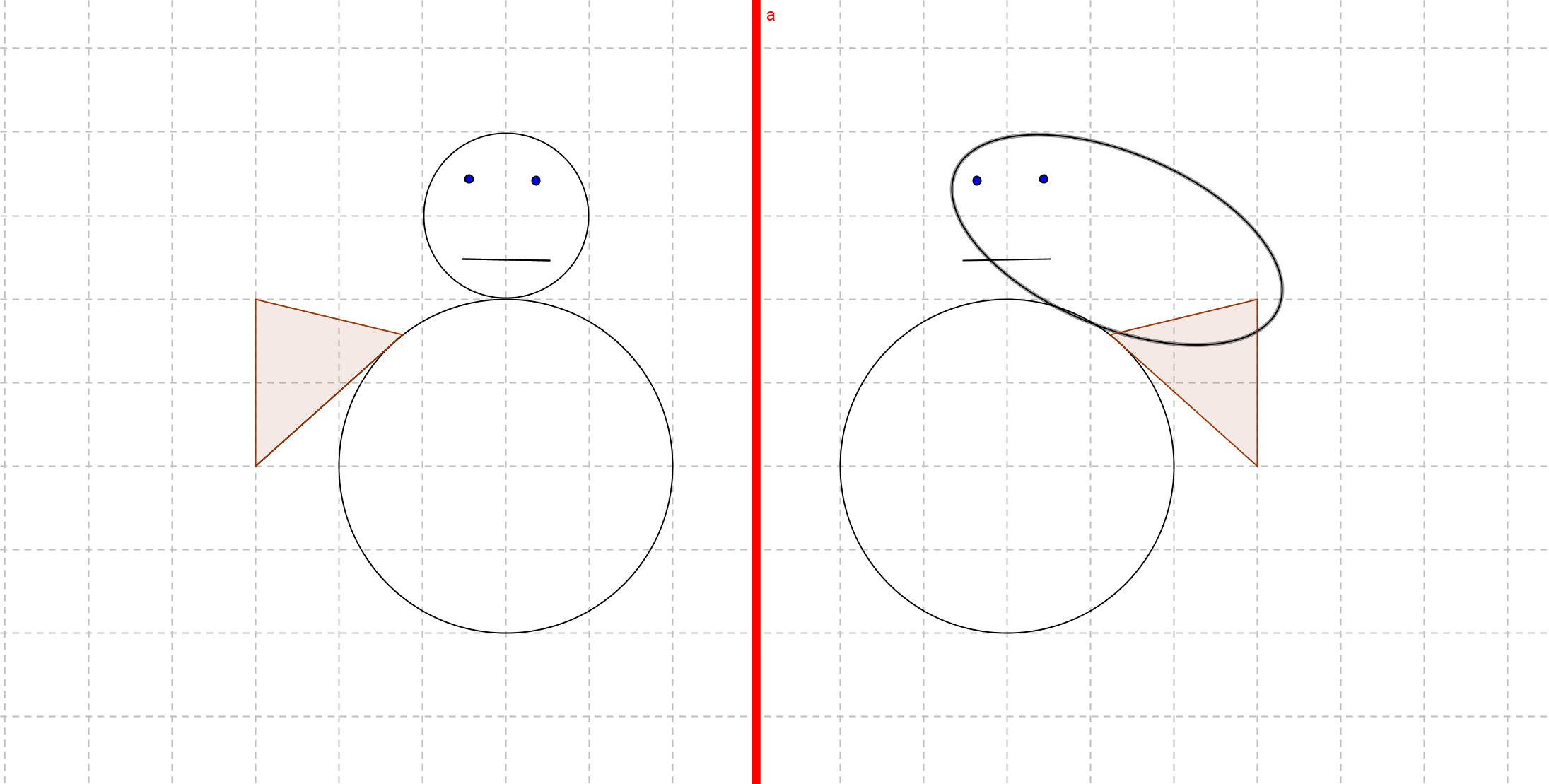
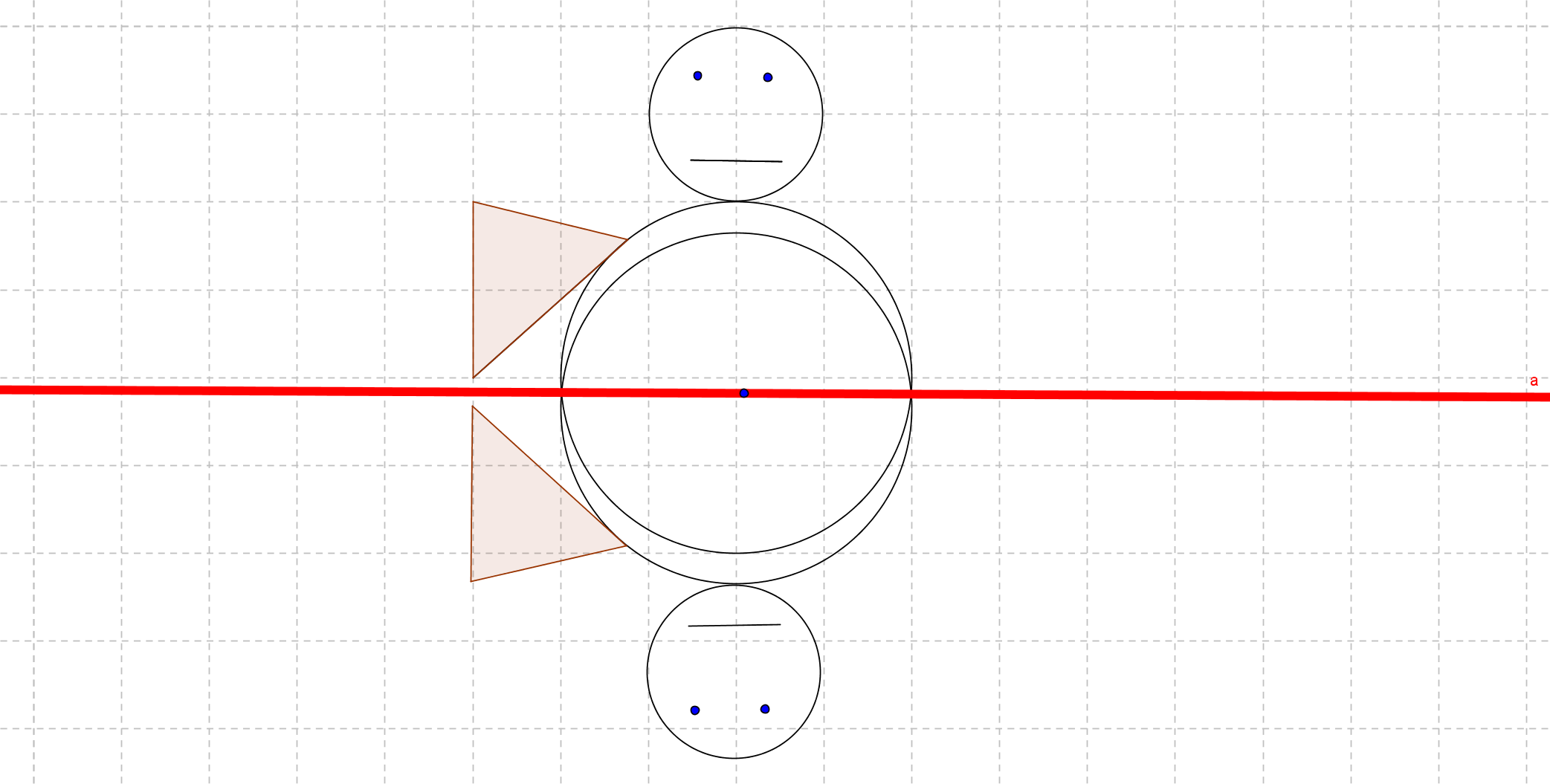
5. Erstelle selbst eine Abbildung nach obigem Vorbild, in dem die Längentreue verletzt ist, jedoch Winkeltreue gilt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Achsenspiegelung
  Individuelle Lösungen…
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
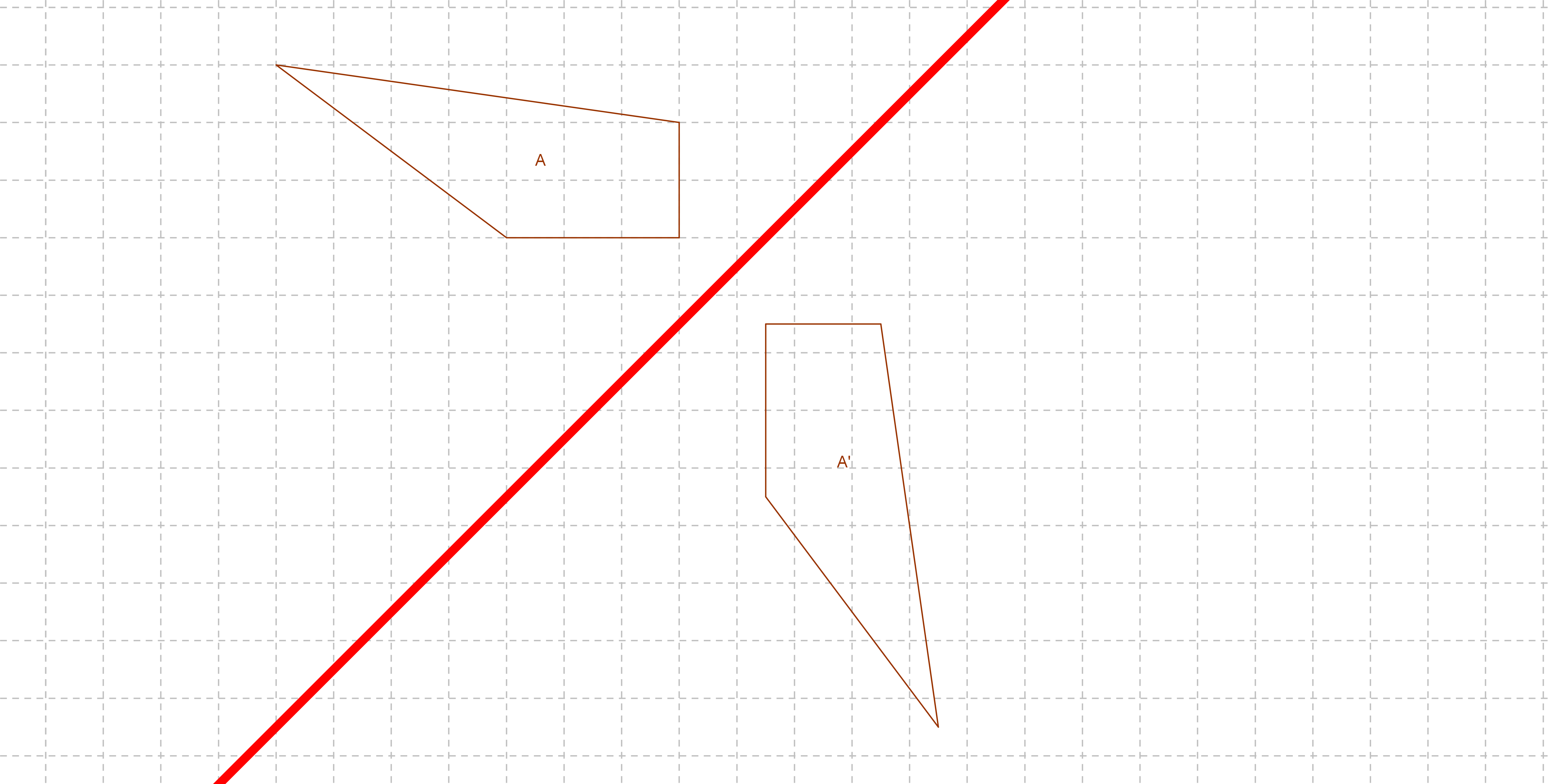
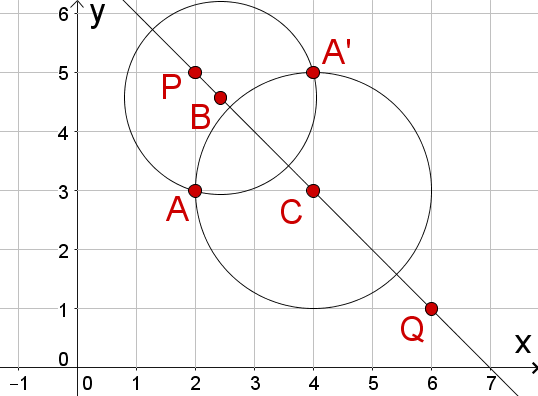
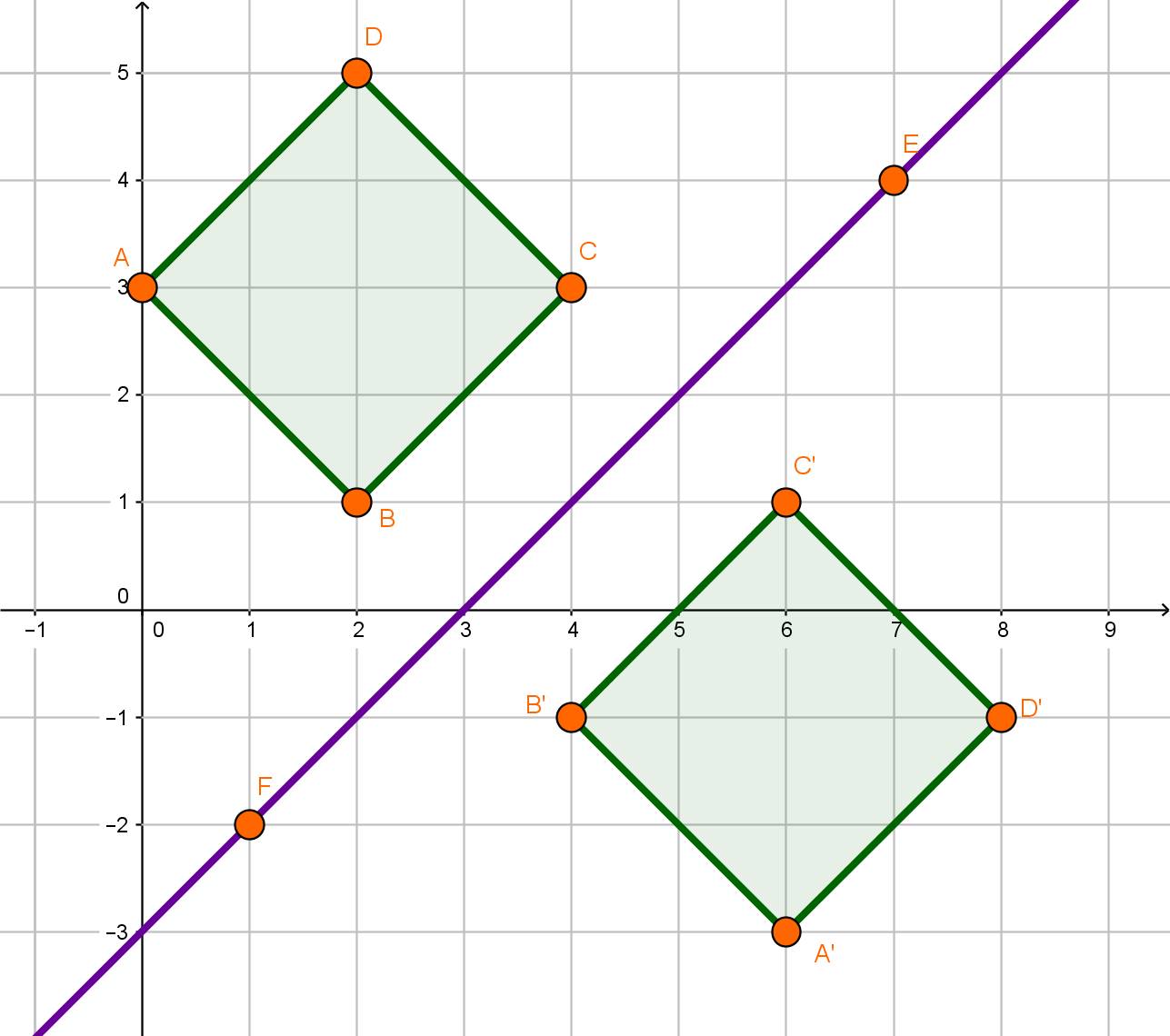
Das Viereck A' ist durch Achsenspiegelung aus dem Viereck A hervorgegangen. Übertrage die Abbildung in dein Heft und zeichne die Spiegelachse ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung
Die Spiegelachse ist rot eingezeichnet.
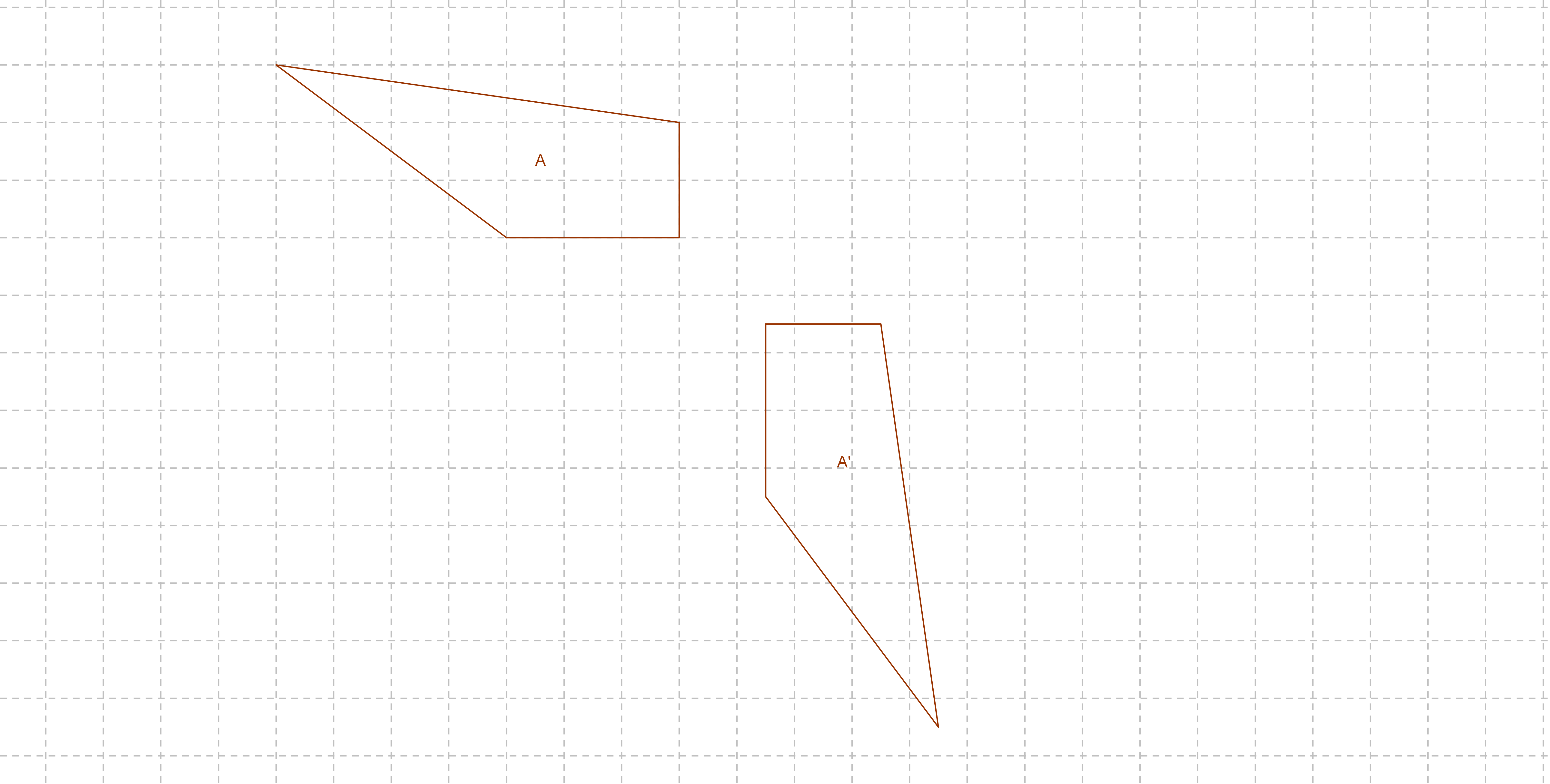
4
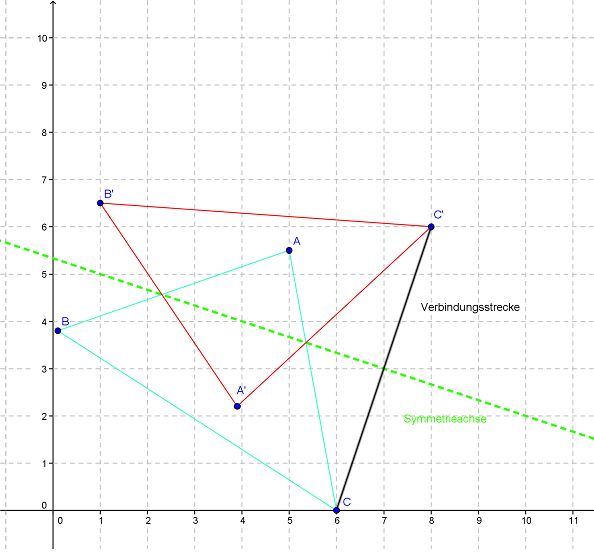
Bilde das Dreieck mit den Eckpunkten $A(1|5{,}5)$ , $B(4{,}5|1)$ und $C(8|3)$ durch Achsenspiegelung an der Geraden $g = PQ$ mit $P(1{,}5|9{,}5)$ und $Q(12|2{,}5)$ ab.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktionsbeschreibung
Spiegele die Punkte A, B und C unter Zuhilfenahme eines Geodreiecks oder nach Konstruktionsbeschreibung.
5
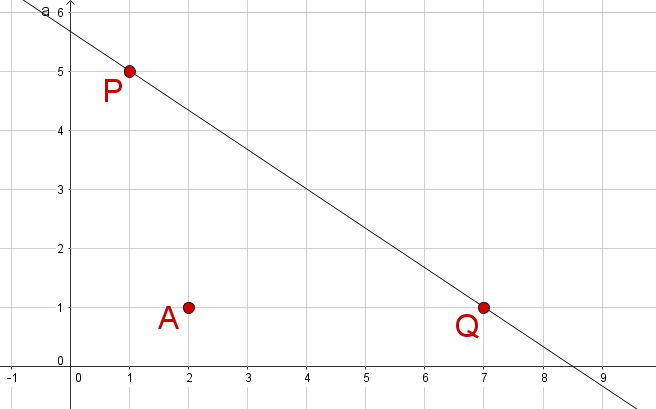
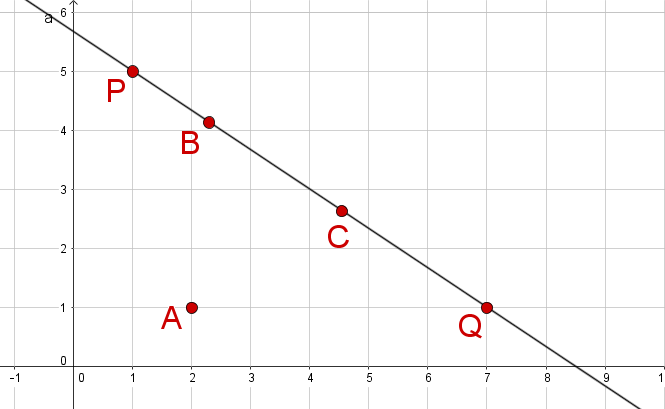
Spiegele die angegebenen Objekte an der Achse durch die Punkte $P$ und $Q$ .
1. Objekt: Punkt $A(2|3)$
  Achse: $P(2|5)$ , $Q(6|1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Achse spiegeln
  Für die Konstruktion wird die Methode mit zwei Hilfskreisen verwendet.
  $A(2|3)$ , $P(2|5)$ , $Q(6|1)$
  $g=PQ$
  Zeichne die drei Punkte $A$ , $P$ , $Q$ in ein Koordinatensystem ein und ziehe die Gerade durch $P$ und $Q$ , um die Spiegelachse einzuzeichnen.
  Suche dir auf der Geraden $PQ$ zwei Punkte (hier $B$ und $C$ )
  Ziehe durch $B$ und $C$ jeweils einen Kreis, der durch $A$ verläuft.
  Der zweite Schnittpunkt der Kreise (zusätzlich zu $A$ ) ist der gesuchte Spiegelpunkt $A'$ .
  In der Abbildung kannst du ablesen, dass $A'$ sich am Punkt $(4|5)$ befinden soll.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Objekt: Punkt $A(2|1)$
  Achse: $P(1|5)$ , $Q(7|1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Achse spiegeln
  Für die Konstruktion wird die Methode mit zwei Hilfskreisen verwendet.
  $A(2|1)$ , $P(1|5)$ , $Q(7|1)$
  $g=PQ$
  Zeichne die drei Punkte $A$ , $P$ , $Q$ in ein Koordinatensystem ein und ziehe die Gerade durch $P$ und $Q$ , um die Spiegelachse einzuzeichnen.
  Suche dir auf der Geraden $PQ$ zwei Punkte (hier $B$ und $C$ )
  Ziehe durch $B$ und $C$ jeweils einen Kreis, der durch $A$ verläuft.
  Der zweite Schnittpunkt der Kreise (zusätzlich zu $A$ ) ist der gesuchte Spiegelpunkt $A'$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Objekt: Dreieck $ABC$ mit $A(4|4)$ , $B(4|1)$ , $C(7|1)$
  Achse: $D(3|5)$ , $E(3|1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Achse spiegeln
  Spiegele die Punkte $A,B$ und $C$ an der Achse $DE$ . Du erhältst:
  $A'(2|4), B'(2|1) , C'(-1|1)$
  Wenn du die drei Punkte $A', B'$ und $C'$ verbindest, erhältst du das gespiegelte Dreieck $A'C'B'$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Objekt: Quadrat $ABCD$ mit $A(0|3) , B(2|1) , C(4|3) , D(2|5)$
  Achse: $F(1|-2) , E(7|4)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkt an Achse spiegeln
  Spiegele die Punkte $A , B , C$ und $D$ . Du erhälst: $A'(6|-3) , B'(4|-1) , C'(6|1)$ und $D'(8|-1)$
  Wenn du die vier Punkte $A′, B′ , C'$ und $D′$ verbindest, erhältst du das gespiegelte Dreieck $A′C′B′D'$ .
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
6
Das Dreieck $∆ ABC$ wird per Achsenspiegelung auf das Dreieck $∆ A'B'C'$ mit $A(5│5{,}5)$ , $C(6│0)$ , $B'(1│6{,}5)$ und $C'(8│6)$ abgebildet.
Bestimme nun die Lage der Eckpunkte $B$ und $A'$ und zeichne beide Dreiecke in ein Koordinatensystem ein.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung
Bestimme die Symmetrieachse als Mittelsenkrechte der Verbindungsstrecke von einem beliebigen Ur- und Bildpunkt.
Diese Ermittlung der Symmetrieachse ist aufgrund der Eigenschaften der Achsenspiegelung (Längen-, Winkel- und Geradentreue) möglich.
Danach werden die gesuchten Spiegelpunkte ermittelt und die Dreiecke eingezeichnet.
7
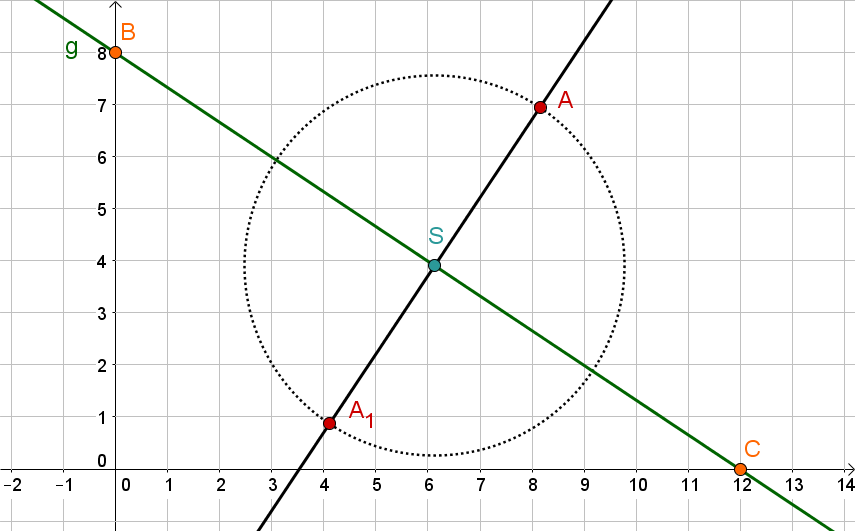
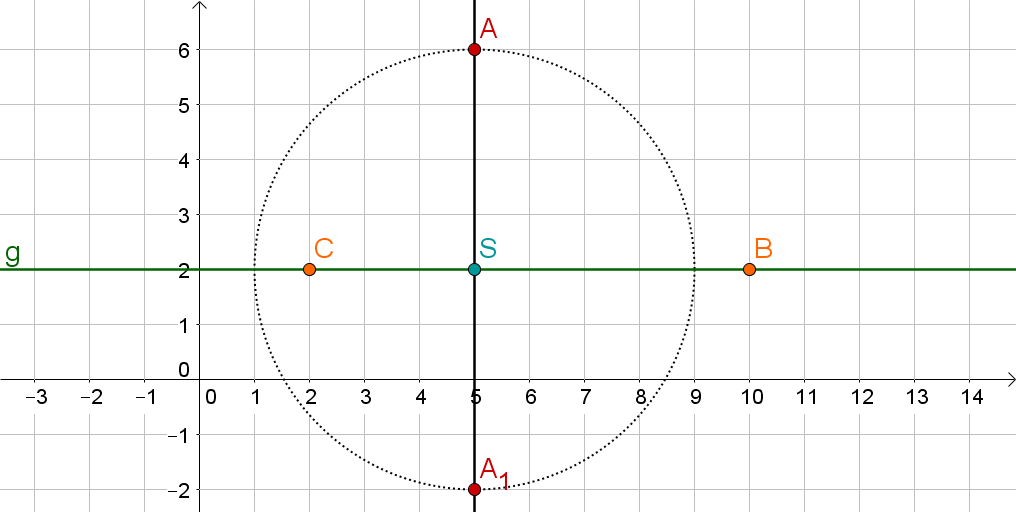
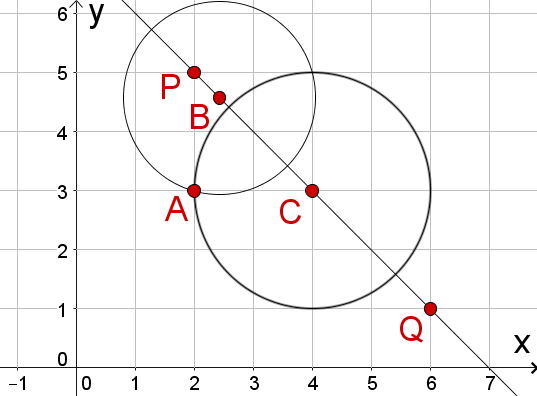
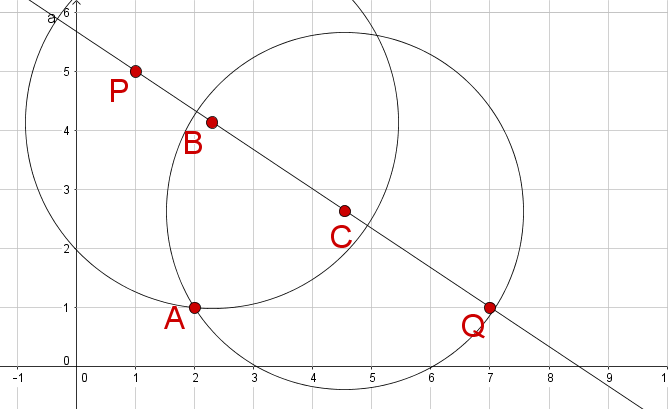
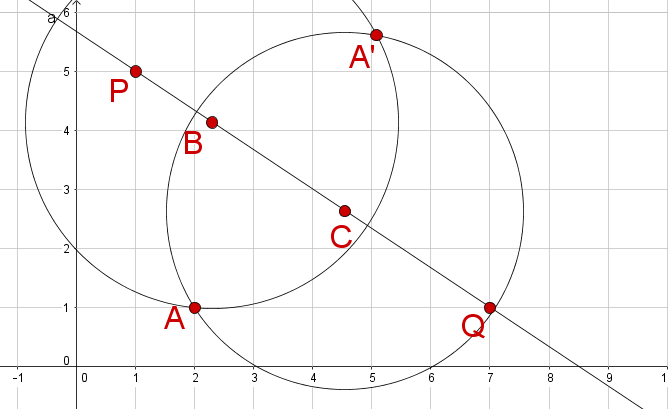
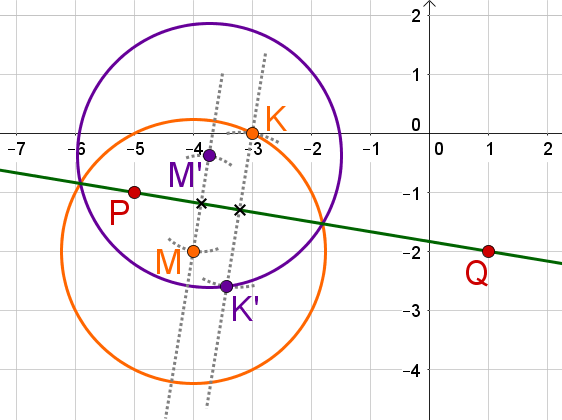
Spiegele den Kreis mit Mittelpunkt $M(-4|-2)$ , der durch den Punkt $K(-3|0)$ verläuft, an der Gerade durch die Punkte $P(-5|-1)$ und $Q(1|-2)$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Figur an Achse spiegeln
Anfangs zeichnest du die Spiegelachse $PQ$ und den Kreis um $M$ durch $K$ in ein Koordinatensystem ein. Anschließend spiegelst du die beiden Punkte $M$ bzw. $K$ an $PQ$ auf $M'$ bzw. $K'$ . Nun kannst du um $M'$ einen Kreis durch $K'$ ziehen und erhältst das gewünschte Ergebnis, das im folgenden Bild zu sehen ist.
Bemerkung:
Um den gespiegelten Kreis um $M'$ zu erhalten, ist es nicht nötig den ursprünglichen Kreis um $M$ einzuzeichnen. Da du nur die beiden Punkte $K$ und $M$ spiegelst, würde es reichen diese beiden einzuzeichnen.
Da du aber viel schneller erkennen kannst, ob deine Lösung richtig ist, solltest du ihn trotzdem einzeichnen.
8
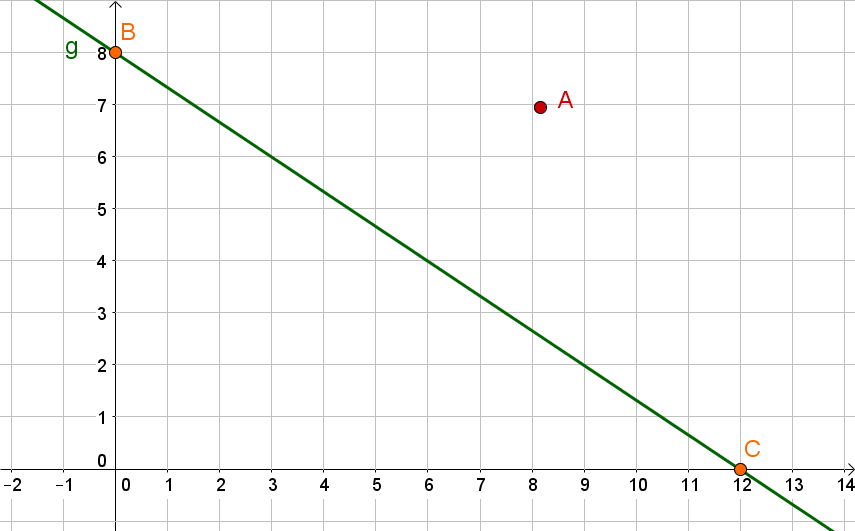
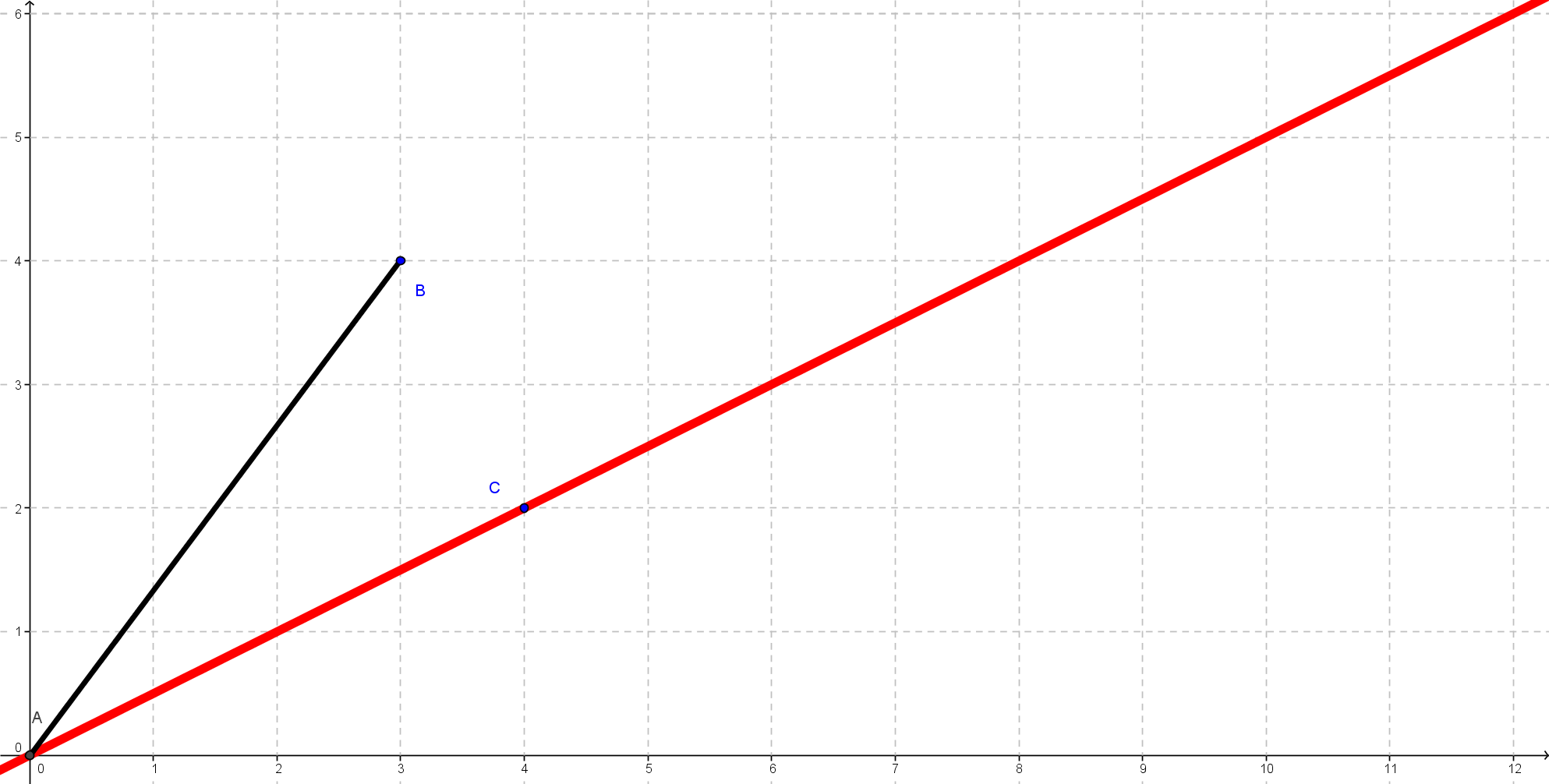
Gegeben sind die Punkte A(0|0), B(3|4) und C(4|2). Ermittle die Länge der Strecke [AB] ohne zu messen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Spiegelung
Spiegelt man die Strecke [AB] an AC, so erhält man die Strecke [AD] mit D(5|0). Damit beträgt die Länge der Strecke [AB] 5 LE. (Längentreue!!)