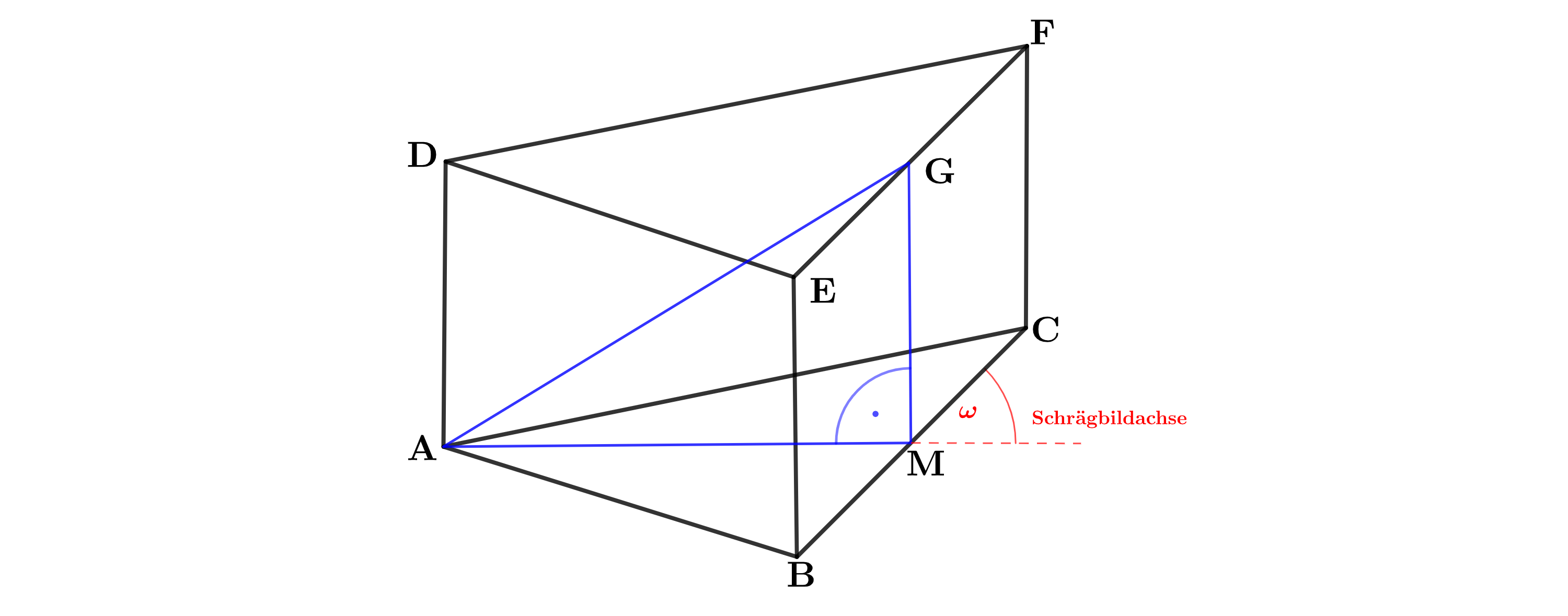
Die nebenstehende Skizze zeigt ein Schrägbild des Prismas , dessen Grundfläche das gleichschenklige Dreieck mit der Basis ist. Der Punkt liegt senkrecht über dem Punkt . Der Punkt ist der Mittelpunkt der Strecke und der Punkt ist der Mittelpunkt der Strecke .
Es gilt:
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Zeichnen Sie das Schrägbild des Prismas , wobei die Strecke auf der Schrägbildachse und der Punkt links von liegen soll.
Für die Zeichnung gilt:
Zeichnen Sie sodann die Strecke in das Schrägbild ein und berechnen Sie deren Länge sowie das Maß des Winkels .
Ergebnis:
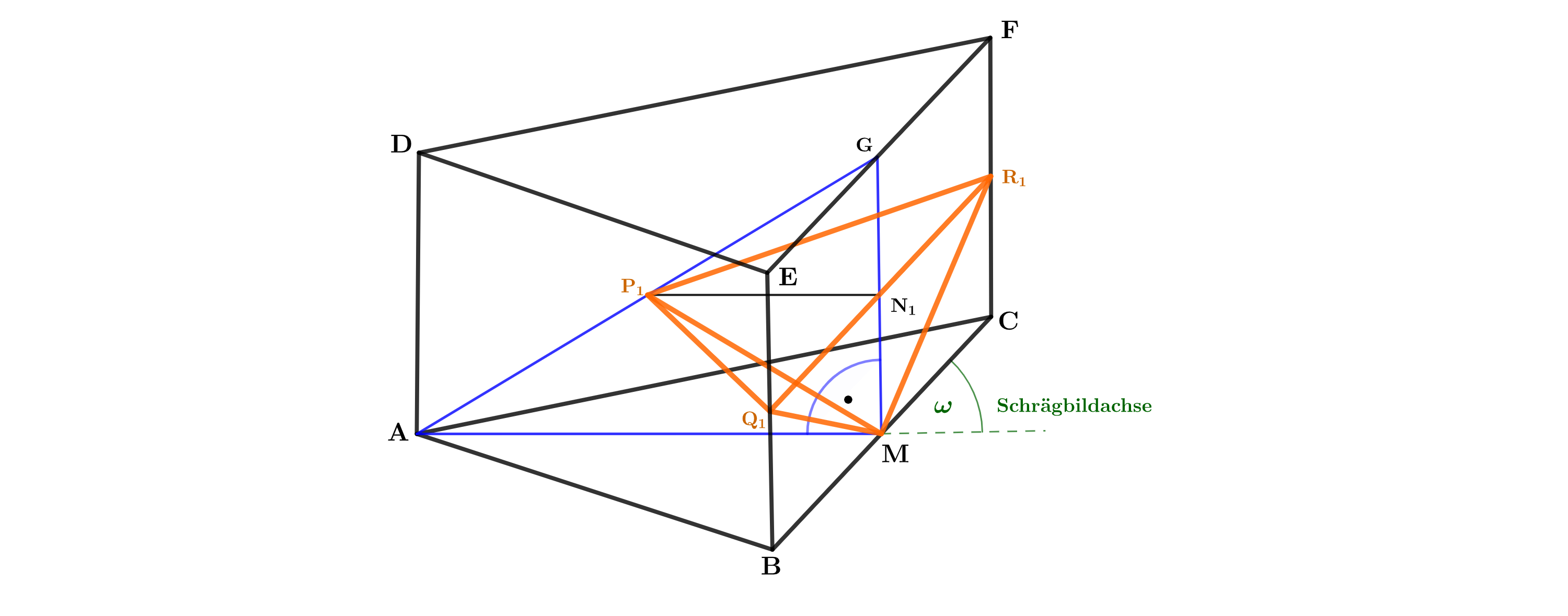
Ebenen, die zur Grundfläche parallel sind, schneiden in Punkten , in Punkten , in Punkten und in Punkten .
Es gilt: mit sowie .
Der Punkt ist die Spitze von Pyramiden mit Dreiecken als Grundfläche.
Zeichnen Sie die Strecke , den Punkt sowie die Pyramide für in das Schrägbild zur Teilaufgabe (a) ein.
Zeigen Sie rechnerisch, dass sich das Volumen der Pyramiden in Abhängigkeit von wie folgt darstellen lässt: .
Teilergebnis:
Unter den Pyramiden hat die Pyramide das maximale Volumen.
Berechnen Sie, um wie viel Prozent das Volumen der Pyramide kleiner ist als das Volumen des Prismas .
Die Pyramiden und haben jeweils ein Volumen von .
Berechnen Sie die zugehörigen Werte für .
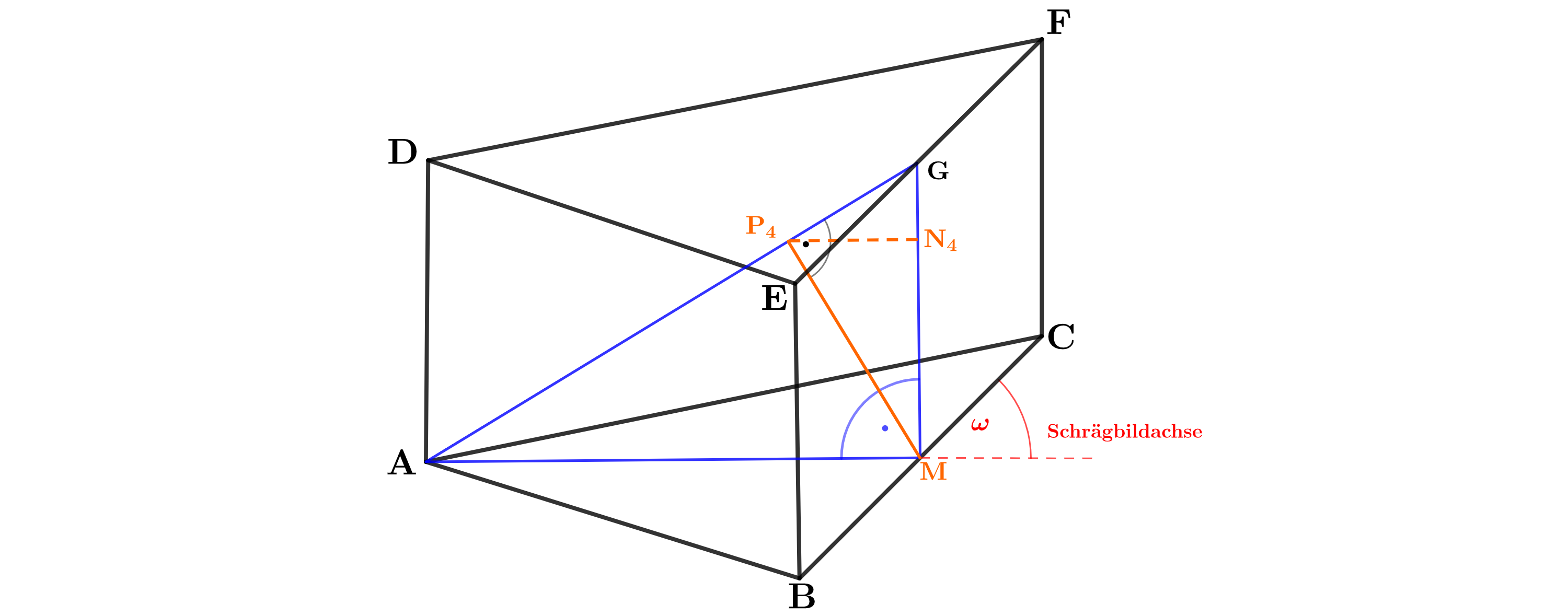
Zeigen Sie, dass für die Längen der Strecken in Abhängigkeit von gilt:
.
Unter den Strecken hat die Strecke die minimale Länge.
Zeichnen Sie die Strecken in das Schrägbild zur Teilaufgabe (a) ein und berechnen Sie deren Länge.